本文主要是介绍代码随想录算法训练营第十九天:二叉树go,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
代码随想录算法训练营第十九天:二叉树go
226.翻转二叉树
力扣题目链接(opens new window)
翻转一棵二叉树。
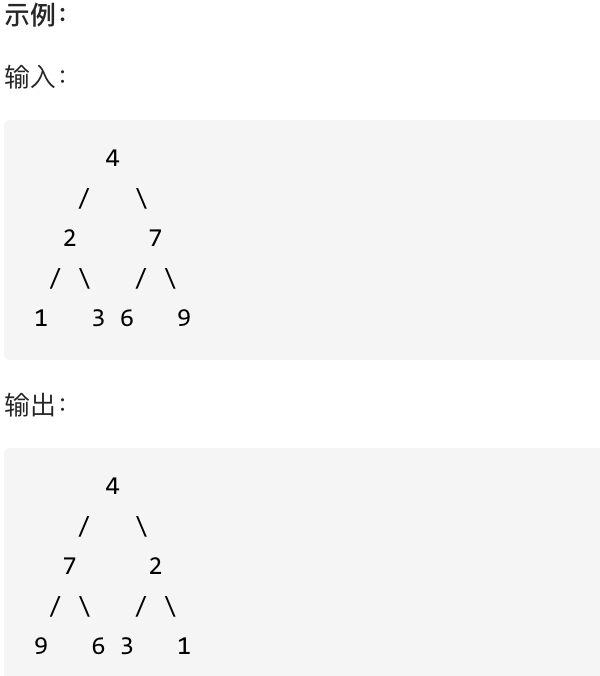
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,权当一个乐子哈)
#算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** :听说一位巨佬面Google被拒了,因为没写出翻转二叉树 | LeetCode:226.翻转二叉树 ****(opens new window)**** ,相信结合视频再看本篇题解,更有助于大家对本题的理解。
#题外话
这道题目是非常经典的题目,也是比较简单的题目(至少一看就会)。
但正是因为这道题太简单,一看就会,一些同学都没有抓住起本质,稀里糊涂的就把这道题目过了。
如果做过这道题的同学也建议认真看完,相信一定有所收获!
#思路
我们之前介绍的都是各种方式遍历二叉树,这次要翻转了,感觉还是有点懵逼。
这得怎么翻转呢?
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
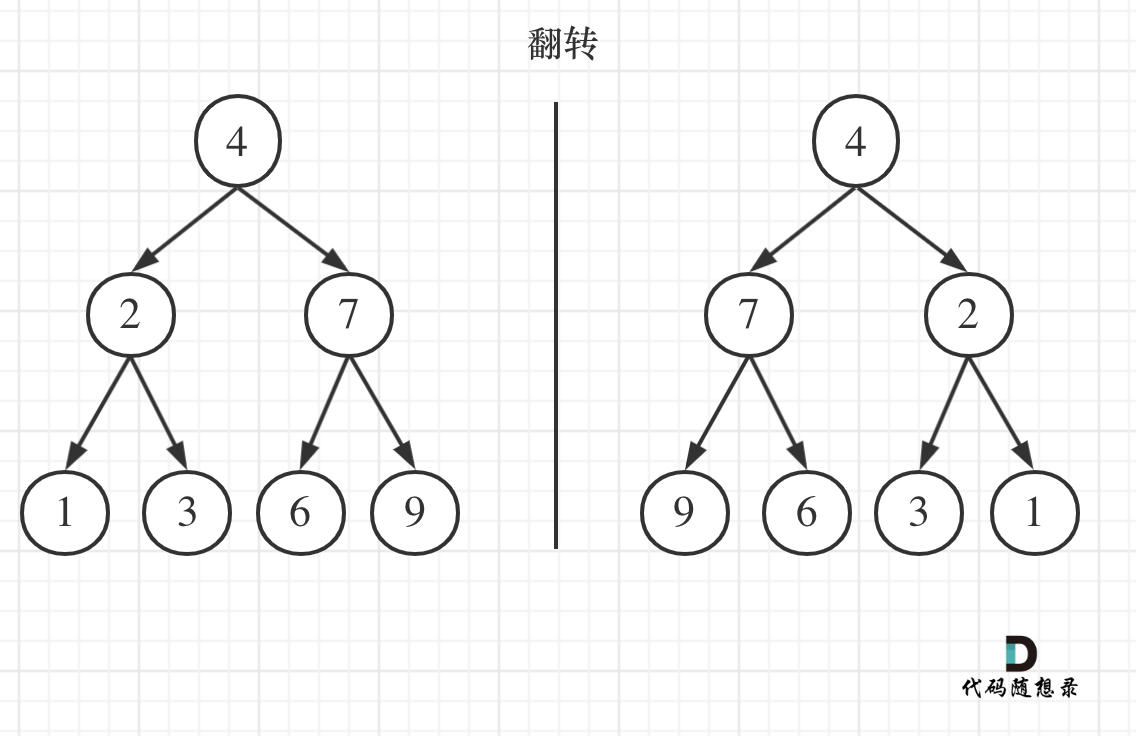
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
关键在于遍历顺序,前中后序应该选哪一种遍历顺序? (一些同学这道题都过了,但是不知道自己用的是什么顺序)
遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。
注意只要把每一个节点的左右孩子翻转一下,就可以达到整体翻转的效果
这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便,因为中序遍历会把某些节点的左右孩子翻转了两次!建议拿纸画一画,就理解了
那么层序遍历可以不可以呢?依然可以的!只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的!
#递归法
对于二叉树的递归法的前中后序遍历,已经在二叉树:前中后序递归遍历 **(opens new window)** 详细讲解了。
我们下文以前序遍历为例,通过动画来看一下翻转的过程:
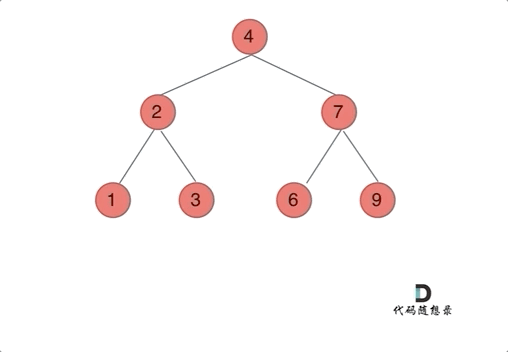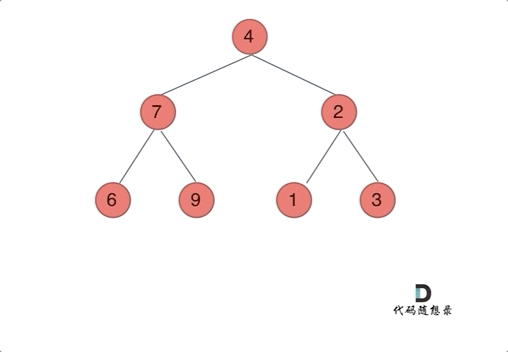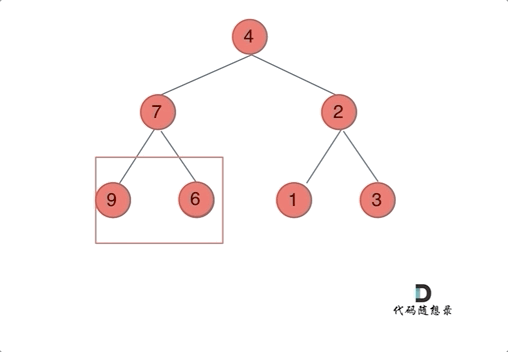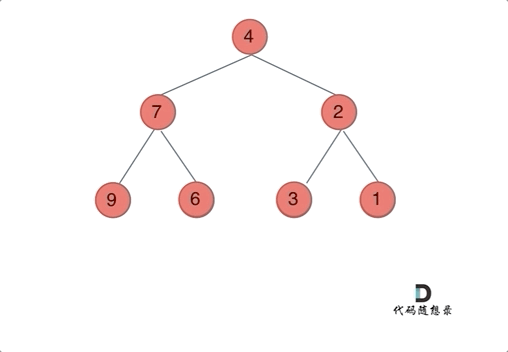
我们来看一下递归三部曲:
- 确定递归函数的参数和返回值
参数就是要传入节点的指针,不需要其他参数了,通常此时定下来主要参数,如果在写递归的逻辑中发现还需要其他参数的时候,随时补充。
返回值的话其实也不需要,但是题目中给出的要返回root节点的指针,可以直接使用题目定义好的函数,所以就函数的返回类型为TreeNode*。
TreeNode* invertTree(TreeNode* root)
- 确定终止条件
当前节点为空的时候,就返回
if (root == NULL) return root;
- 确定单层递归的逻辑
因为是先前序遍历,所以先进行交换左右孩子节点,然后反转左子树,反转右子树。
swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);
基于这递归三步法,代码基本写完,C++代码如下:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;swap(root->left, root->right); // 中invertTree(root->left); // 左invertTree(root->right); // 右return root;}
};
#迭代法
#深度优先遍历
二叉树:听说递归能做的,栈也能做! **(opens new window)** 中给出了前中后序迭代方式的写法,所以本题可以很轻松的写出如下迭代法的代码:
C++代码迭代法(前序遍历)
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;stack<TreeNode*> st;st.push(root);while(!st.empty()) {TreeNode* node = st.top(); // 中st.pop();swap(node->left, node->right);if(node->right) st.push(node->right); // 右if(node->left) st.push(node->left); // 左}return root;}
};
如果这个代码看不懂的话可以再回顾一下二叉树:听说递归能做的,栈也能做! **(opens new window)** 。
我们在二叉树:前中后序迭代方式的统一写法 **(opens new window)** 中介绍了统一的写法,所以,本题也只需将文中的代码少做修改便可。
C++代码如下迭代法(前序遍历)
class Solution {
public:TreeNode* invertTree(TreeNode* root) {stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();if (node->right) st.push(node->right); // 右if (node->left) st.push(node->left); // 左st.push(node); // 中st.push(NULL);} else {st.pop();node = st.top();st.pop();swap(node->left, node->right); // 节点处理逻辑}}return root;}
};class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == nullptr) return nullptr;TreeNode* tmp = root->left;root->left = invertTree(root->right);root->right = invertTree(tmp);return root;}
};如果上面这个代码看不懂,回顾一下文章二叉树:前中后序迭代方式的统一写法 **(opens new window)** 。
#广度优先遍历
也就是层序遍历,层数遍历也是可以翻转这棵树的,因为层序遍历也可以把每个节点的左右孩子都翻转一遍,代码如下:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);while (!que.empty()) {int size = que.size();for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();swap(node->left, node->right); // 节点处理if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return root;}
};
如果对以上代码不理解,或者不清楚二叉树的层序遍历,可以看这篇二叉树:层序遍历登场!(opens new window)
#拓展
文中我指的是递归的中序遍历是不行的,因为使用递归的中序遍历,某些节点的左右孩子会翻转两次。
如果非要使用递归中序的方式写,也可以,如下代码就可以避免节点左右孩子翻转两次的情况:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;invertTree(root->left); // 左swap(root->left, root->right); // 中invertTree(root->left); // 注意 这里依然要遍历左孩子,因为中间节点已经翻转了return root;}
};
代码虽然可以,但这毕竟不是真正的递归中序遍历了。
但使用迭代方式统一写法的中序是可以的。
代码如下:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();if (node->right) st.push(node->right); // 右st.push(node); // 中st.push(NULL);if (node->left) st.push(node->left); // 左} else {st.pop();node = st.top();st.pop();swap(node->left, node->right); // 节点处理逻辑}}return root;}
};为什么这个中序就是可以的呢,因为这是用栈来遍历,而不是靠指针来遍历,避免了递归法中翻转了两次的情况,大家可以画图理解一下,这里有点意思的。
#总结
针对二叉树的问题,解题之前一定要想清楚究竟是前中后序遍历,还是层序遍历。
二叉树解题的大忌就是自己稀里糊涂的过了(因为这道题相对简单),但是也不知道自己是怎么遍历的。
这也是造成了二叉树的题目“一看就会,一写就废”的原因。
针对翻转二叉树,我给出了一种递归,三种迭代(两种模拟深度优先遍历,一种层序遍历)的写法,都是之前我们讲过的写法,融汇贯通一下而已。
大家一定也有自己的解法,但一定要成方法论,这样才能通用,才能举一反三
周一
本周我们开始讲解了二叉树,在关于二叉树,你该了解这些! **(opens new window)** 中讲解了二叉树的理论基础。
有同学会把红黑树和二叉平衡搜索树弄分开了,其实红黑树就是一种二叉平衡搜索树,这两个树不是独立的,所以C++中map、multimap、set、multiset的底层实现机制是二叉平衡搜索树,再具体一点是红黑树。
对于二叉树节点的定义,C++代码如下:
struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
对于这个定义中TreeNode(int x) : val(x), left(NULL), right(NULL) {} 有同学不清楚干什么的。
这是构造函数,这么说吧C语言中的结构体是C++中类的祖先,所以C++结构体也可以有构造函数。
构造函数也可以不写,但是new一个新的节点的时候就比较麻烦。
例如有构造函数,定义初始值为9的节点:
TreeNode* a = new TreeNode(9);
没有构造函数的话就要这么写:
TreeNode* a = new TreeNode();
a->val = 9;
a->left = NULL;
a->right = NULL;
在介绍前中后序遍历的时候,有递归和迭代(非递归),还有一种牛逼的遍历方式:morris遍历。
morris遍历是二叉树遍历算法的超强进阶算法,morris遍历可以将非递归遍历中的空间复杂度降为O(1),感兴趣大家就去查一查学习学习,比较小众,面试几乎不会考。我其实也没有研究过,就不做过多介绍了。
#周二
在二叉树:一入递归深似海,从此offer是路人 **(opens new window)** 中讲到了递归三要素,以及前中后序的递归写法。
文章中我给出了leetcode上三道二叉树的前中后序题目,但是看完二叉树:一入递归深似海,从此offer是路人 **(opens new window)** ,依然可以解决n叉树的前后序遍历,在leetcode上分别是
- 589. N叉树的前序遍历(opens new window)
- 590. N叉树的后序遍历(opens new window)
大家可以再去把这两道题目做了。
#周三
在二叉树:听说递归能做的,栈也能做! **(opens new window)** 中我们开始用栈来实现递归的写法,也就是所谓的迭代法。
细心的同学发现文中前后序遍历空节点是否入栈写法是不同的
其实空节点入不入栈都差不多,但感觉空节点不入栈确实清晰一些,符合文中动画的演示。
拿前序遍历来举例,空节点入栈:
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;st.push(root);while (!st.empty()) {TreeNode* node = st.top(); // 中st.pop();if (node != NULL) result.push_back(node->val);else continue;st.push(node->right); // 右st.push(node->left); // 左}return result;}
};
前序遍历空节点不入栈的代码:(注意注释部分和上文的区别)
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top(); // 中st.pop();result.push_back(node->val);if (node->right) st.push(node->right); // 右(空节点不入栈)if (node->left) st.push(node->left); // 左(空节点不入栈)}return result;}
};
在实现迭代法的过程中,有同学问了:递归与迭代究竟谁优谁劣呢?
从时间复杂度上其实迭代法和递归法差不多(在不考虑函数调用开销和函数调用产生的堆栈开销),但是空间复杂度上,递归开销会大一些,因为递归需要系统堆栈存参数返回值等等。
递归更容易让程序员理解,但收敛不好,容易栈溢出。
这么说吧,递归是方便了程序员,难为了机器(各种保存参数,各种进栈出栈)。
在实际项目开发的过程中我们是要尽量避免递归!因为项目代码参数、调用关系都比较复杂,不容易控制递归深度,甚至会栈溢出。
#周四
在二叉树:前中后序迭代方式的写法就不能统一一下么? **(opens new window)** 中我们使用空节点作为标记,给出了统一的前中后序迭代法。
此时又多了一种前中后序的迭代写法,那么有同学问了:前中后序迭代法是不是一定要统一来写,这样才算是规范。
其实没必要,还是自己感觉哪一种更好记就用哪种。
但是一定要掌握前中后序一种迭代的写法,并不因为某种场景的题目一定要用迭代,而是现场面试的时候,面试官看你顺畅的写出了递归,一般会进一步考察能不能写出相应的迭代。
#周五
在二叉树:层序遍历登场! **(opens new window)** 中我们介绍了二叉树的另一种遍历方式(图论中广度优先搜索在二叉树上的应用)即:层序遍历。
看完这篇文章,去leetcode上怒刷五题,文章中 编号107题目的样例图放错了(原谅我匆忙之间总是手抖),但不影响大家理解。
只有同学发现leetcode上“515. 在每个树行中找最大值”,也是层序遍历的应用,依然可以分分钟解决,所以就是一鼓作气解决六道了。
层序遍历遍历相对容易一些,只要掌握基本写法(也就是框架模板),剩下的就是在二叉树每一行遍历的时候做做逻辑修改。
#周六
在二叉树:你真的会翻转二叉树么? **(opens new window)** 中我们把翻转二叉树这么一道简单又经典的问题,充分的剖析了一波,相信就算做过这道题目的同学,看完本篇之后依然有所收获!
文中我指的是递归的中序遍历是不行的,因为使用递归的中序遍历,某些节点的左右孩子会翻转两次。
如果非要使用递归中序的方式写,也可以,如下代码就可以避免节点左右孩子翻转两次的情况:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;invertTree(root->left); // 左swap(root->left, root->right); // 中invertTree(root->left); // 注意 这里依然要遍历左孩子,因为中间节点已经翻转了return root;}
};
代码虽然可以,但这毕竟不是真正的递归中序遍历了。
但使用迭代方式统一写法的中序是可以的。
代码如下:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();if (node->right) st.push(node->right); // 右st.push(node); // 中st.push(NULL);if (node->left) st.push(node->left); // 左} else {st.pop();node = st.top();st.pop();swap(node->left, node->right); // 节点处理逻辑}}return root;}
};为什么这个中序就是可以的呢,因为这是用栈来遍历,而不是靠指针来遍历,避免了递归法中翻转了两次的情况,大家可以画图理解一下,这里有点意思的。
#总结
本周我们都是讲解了二叉树,从理论基础到遍历方式,从递归到迭代,从深度遍历到广度遍历,最后再用了一个翻转二叉树的题目把我们之前讲过的遍历方式都串了起来。

101. 对称二叉树
力扣题目链接(opens new window)
给定一个二叉树,检查它是否是镜像对称的。

#算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** :同时操作两个二叉树 | LeetCode:101. 对称二叉树 ****(opens new window)**** , 相信结合视频再看本篇题解,更有助于大家对本题的理解。
#思路
首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!
对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了其实我们要比较的是两个树(这两个树是根节点的左右子树) ,所以在递归遍历的过程中,也是要同时遍历两棵树。
那么如何比较呢?
比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
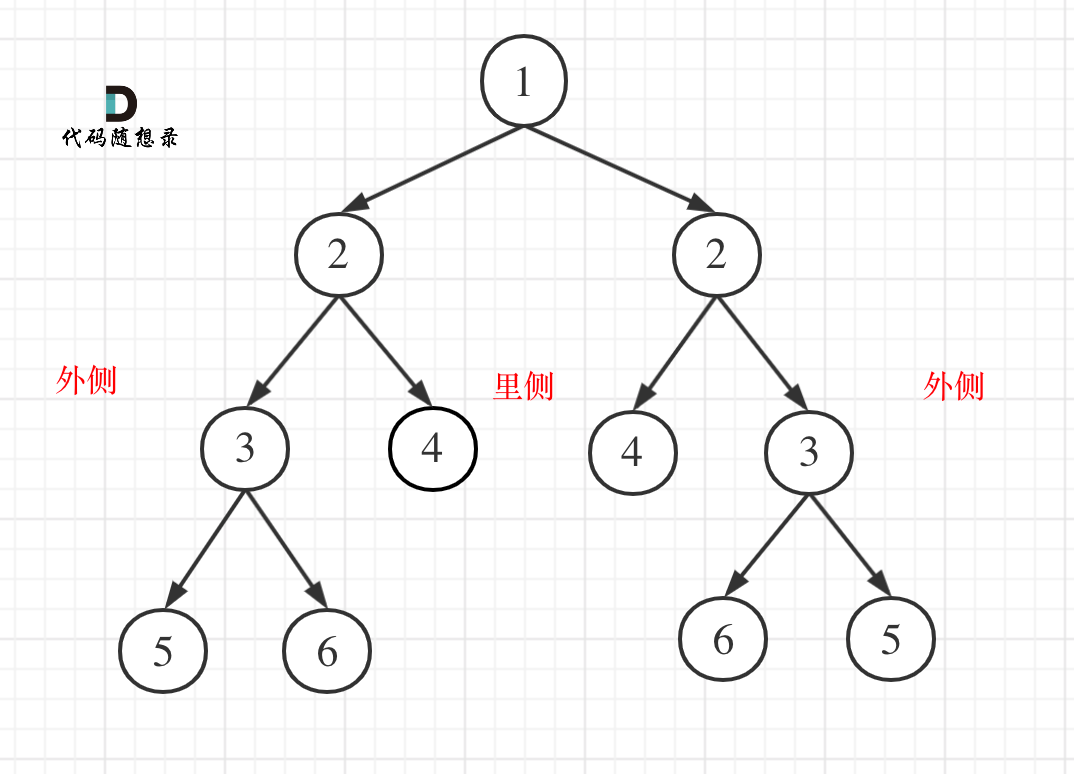
那么遍历的顺序应该是什么样的呢?
本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。
但都可以理解算是后序遍历,尽管已经不是严格上在一个树上进行遍历的后序遍历了。
其实后序也可以理解为是一种回溯,当然这是题外话,讲回溯的时候会重点讲的。
说到这大家可能感觉我有点啰嗦,哪有这么多道理,上来就干就完事了。别急,我说的这些在下面的代码讲解中都有身影。
那么我们先来看看递归法的代码应该怎么写。
#递归法
递归三部曲
- 确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
返回值自然是bool类型。
代码如下:
bool compare(TreeNode* left, TreeNode* right)
- 确定终止条件
要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
节点为空的情况有:(注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点)
- 左节点为空,右节点不为空,不对称,return false
- 左不为空,右为空,不对称 return false
- 左右都为空,对称,返回true
此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
- 左右都不为空,比较节点数值,不相同就return false
此时左右节点不为空,且数值也不相同的情况我们也处理了。
代码如下:
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else
注意上面最后一种情况,我没有使用else,而是else if, 因为我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
- 确定单层递归的逻辑
此时才进入单层递归的逻辑,单层递归的逻辑就是处理 左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内侧是否对称,传入左节点的右孩子,右节点的左孩子。
- 如果左右都对称就返回true ,有一侧不对称就返回false 。
代码如下:
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
return isSame;
如上代码中,我们可以看出使用的遍历方式,左子树左右中,右子树右左中,所以我把这个遍历顺序也称之为“后序遍历”(尽管不是严格的后序遍历)。
最后递归的C++整体代码如下:
class Solution{
public:bool compare(TreeNode* left,TreeNode* right){if(left == NULL && right != NULL)return false;else if(left != NULL && right == NULL)return false;else if (left == NULL && right == NULL)return true;else if(left->val != right -> val)return false;bool outside = compare(left->left,right->right);bool inside = compare(left->right,right->left);bool isSame outside && inside; // 左子树:中、 右子树:中 (逻辑处理)return isSame;}bool isSymmetric(TreeNode* root) {if (root == NULL) return true;return compare(root->left, root->right);}
};迭代法
这道题目我们也可以使用迭代法,但要注意,这里的迭代法可不是前中后序的迭代写法,因为本题的本质是判断两个树是否是相互翻转的,其实已经不是所谓二叉树遍历的前中后序的关系了。
这里我们可以使用队列来比较两个树(根节点的左右子树)是否相互翻转,(注意这不是层序遍历)
#使用队列
通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等,如动画所示:
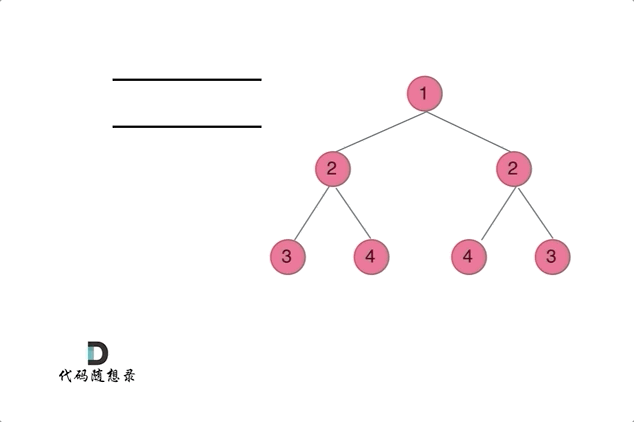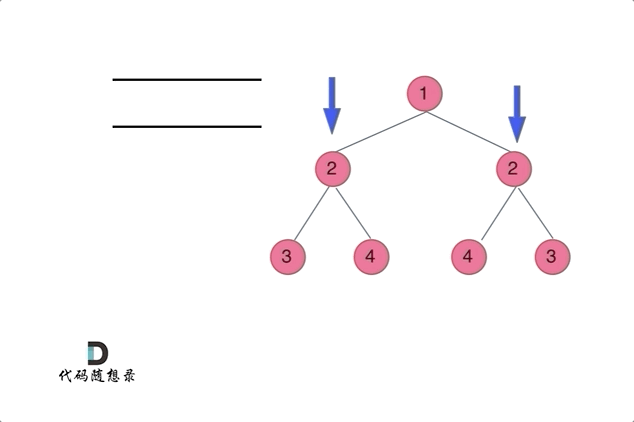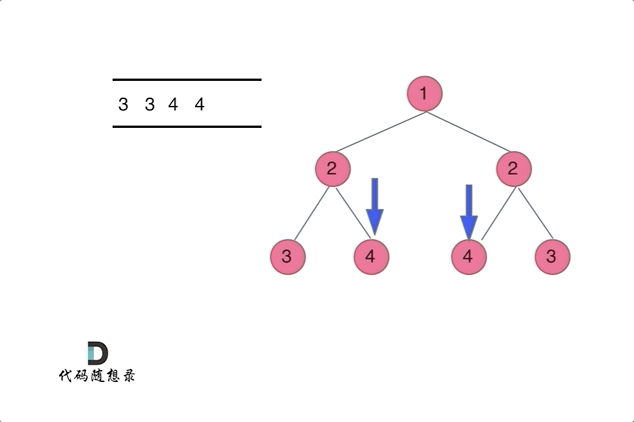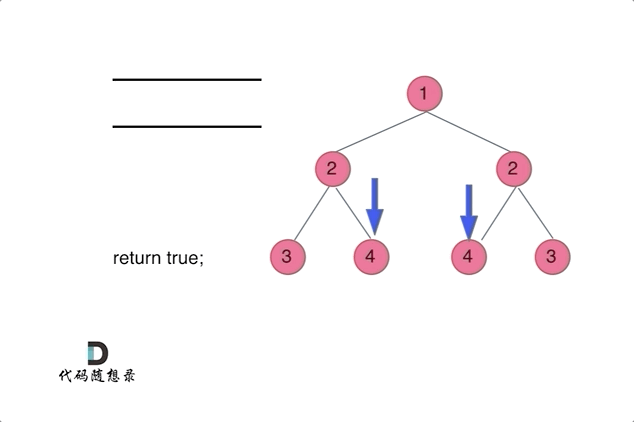
如下的条件判断和递归的逻辑是一样的。
代码如下:
class Solution {
public:bool isSymmetric(TreeNode* root) {if (root == NULL) return true;queue<TreeNode*> que;que.push(root->left); // 将左子树头结点加入队列que.push(root->right); // 将右子树头结点加入队列while (!que.empty()) { // 接下来就要判断这两个树是否相互翻转TreeNode* leftNode = que.front(); que.pop();TreeNode* rightNode = que.front(); que.pop();if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是对称的continue;}// 左右一个节点不为空,或者都不为空但数值不相同,返回falseif ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {return false;}que.push(leftNode->left); // 加入左节点左孩子que.push(rightNode->right); // 加入右节点右孩子que.push(leftNode->right); // 加入左节点右孩子que.push(rightNode->left); // 加入右节点左孩子}return true;}
};
#使用栈
细心的话,其实可以发现,这个迭代法,其实是把左右两个子树要比较的元素顺序放进一个容器,然后成对成对的取出来进行比较,那么其实使用栈也是可以的。
只要把队列原封不动的改成栈就可以了,我下面也给出了代码。
class Solution {
public:bool isSymmetric(TreeNode* root) {if (root == NULL) return true;stack<TreeNode*> st; // 这里改成了栈st.push(root->left);st.push(root->right);while (!st.empty()) {TreeNode* leftNode = st.top(); st.pop();TreeNode* rightNode = st.top(); st.pop();if (!leftNode && !rightNode) {continue;}if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {return false;}st.push(leftNode->left);st.push(rightNode->right);st.push(leftNode->right);st.push(rightNode->left);}return true;}
};
#总结
这次我们又深度剖析了一道二叉树的“简单题”,大家会发现,真正的把题目搞清楚其实并不简单,leetcode上accept了和真正掌握了还是有距离的。
我们介绍了递归法和迭代法,递归依然通过递归三部曲来解决了这道题目,如果只看精简的代码根本看不出来递归三部曲是如何解题的。
在迭代法中我们使用了队列,需要注意的是这不是层序遍历,而且仅仅通过一个容器来成对的存放我们要比较的元素,知道这一本质之后就发现,用队列,用栈,甚至用数组,都是可以的。
如果已经做过这道题目的同学,读完文章可以再去看看这道题目,思考一下,会有不一样的发现!
222.完全二叉树的节点个数
力扣题目链接(opens new window)
给出一个完全二叉树,求出该树的节点个数。
示例 1:
- 输入:root = [1,2,3,4,5,6]
- 输出:6
示例 2:
- 输入:root = []
- 输出:0
示例 3:
- 输入:root = [1]
- 输出:1
提示:
- 树中节点的数目范围是[0, 5 * 10^4]
- 0 <= Node.val <= 5 * 10^4
- 题目数据保证输入的树是 完全二叉树
#算法公开课
《代码随想录》算法视频公开课 ****(opens new window)**** :要理解普通二叉树和完全二叉树的区别! | LeetCode:222.完全二叉树节点的数量 ****(opens new window)**** ,相信结合视频再看本篇题解,更有助于大家对本题的理解。
#思路
本篇给出按照普通二叉树的求法以及利用完全二叉树性质的求法。
#普通二叉树
首先按照普通二叉树的逻辑来求。
这道题目的递归法和求二叉树的深度写法类似, 而迭代法,二叉树:层序遍历登场! **(opens new window)** 遍历模板稍稍修改一下,记录遍历的节点数量就可以了。
递归遍历的顺序依然是后序(左右中)。
#递归
如果对求二叉树深度还不熟悉的话,看这篇:二叉树:看看这些树的最大深度 **(opens new window)** 。
- 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回以该节点为根节点二叉树的节点数量,所以返回值为int类型。
代码如下:
int getNodesNum(TreeNode* cur) {
- 确定终止条件:如果为空节点的话,就返回0,表示节点数为0。
代码如下:
if (cur == NULL) return 0;
- 确定单层递归的逻辑:先求它的左子树的节点数量,再求右子树的节点数量,最后取总和再加一 (加1是因为算上当前中间节点)就是目前节点为根节点的节点数量。
代码如下:
int leftNum = getNodesNum(cur->left); // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum = leftNum + rightNum + 1; // 中
return treeNum;
所以整体C++代码如下:
// 版本一
class Solution {
private:int getNodesNum(TreeNode* cur) {if (cur == NULL) return 0;int leftNum = getNodesNum(cur->left); // 左int rightNum = getNodesNum(cur->right); // 右int treeNum = leftNum + rightNum + 1; // 中return treeNum;}
public:int countNodes(TreeNode* root) {return getNodesNum(root);}
};
代码精简之后C++代码如下:
// 版本二
class Solution {
public:int countNodes(TreeNode* root) {if (root == NULL) return 0;return 1 + countNodes(root->left) + countNodes(root->right);}
};
- 时间复杂度:O(n)
- 空间复杂度:O(log n),算上了递归系统栈占用的空间
网上基本都是这个精简的代码版本,其实不建议大家照着这个来写,代码确实精简,但隐藏了一些内容,连遍历的顺序都看不出来,所以初学者建议学习版本一的代码,稳稳的打基础。
#迭代
如果对求二叉树层序遍历还不熟悉的话,看这篇:二叉树:层序遍历登场! **(opens new window)** 。
那么只要模板少做改动,加一个变量result,统计节点数量就可以了
class Solution {
public:int countNodes(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);int result = 0;while (!que.empty()) {int size = que.size();for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();result++; // 记录节点数量if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return result;}
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
#完全二叉树
以上方法都是按照普通二叉树来做的,对于完全二叉树特性不了解的同学可以看这篇 关于二叉树,你该了解这些! **(opens new window)** ,这篇详细介绍了各种二叉树的特性。
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
我来举一个典型的例子如题:
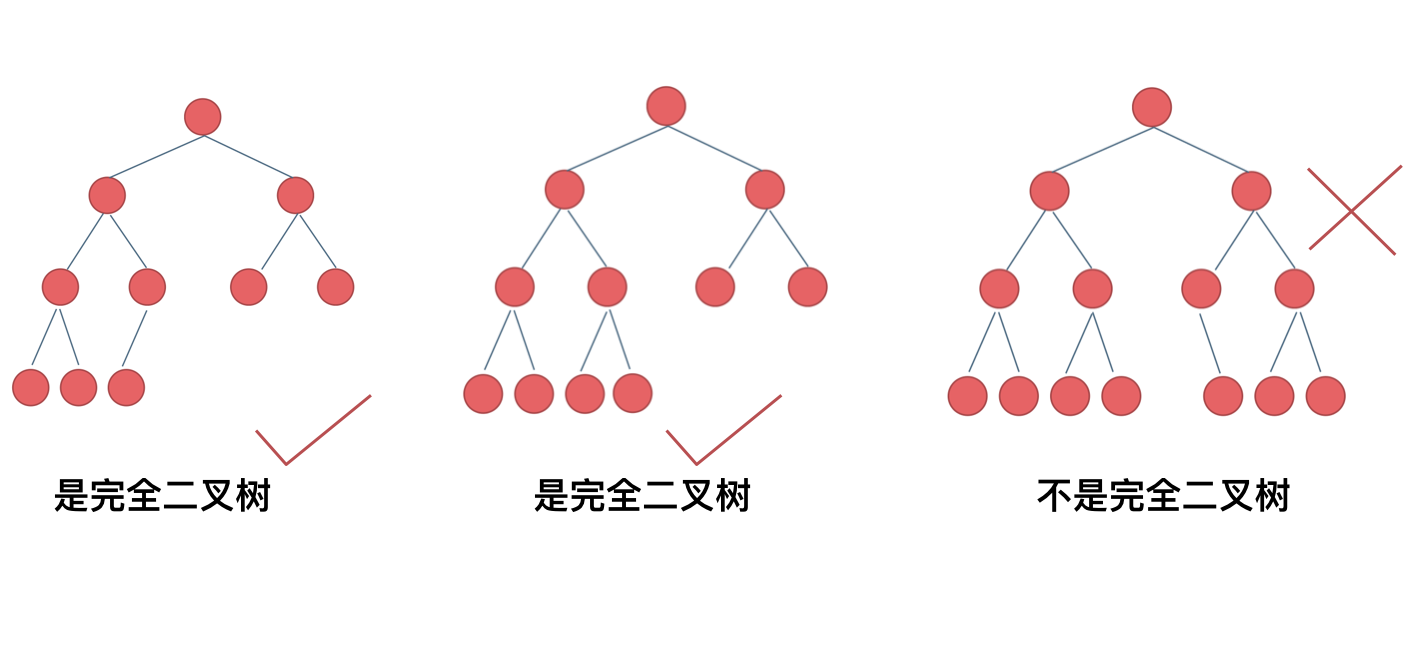
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
完全二叉树(一)如图: 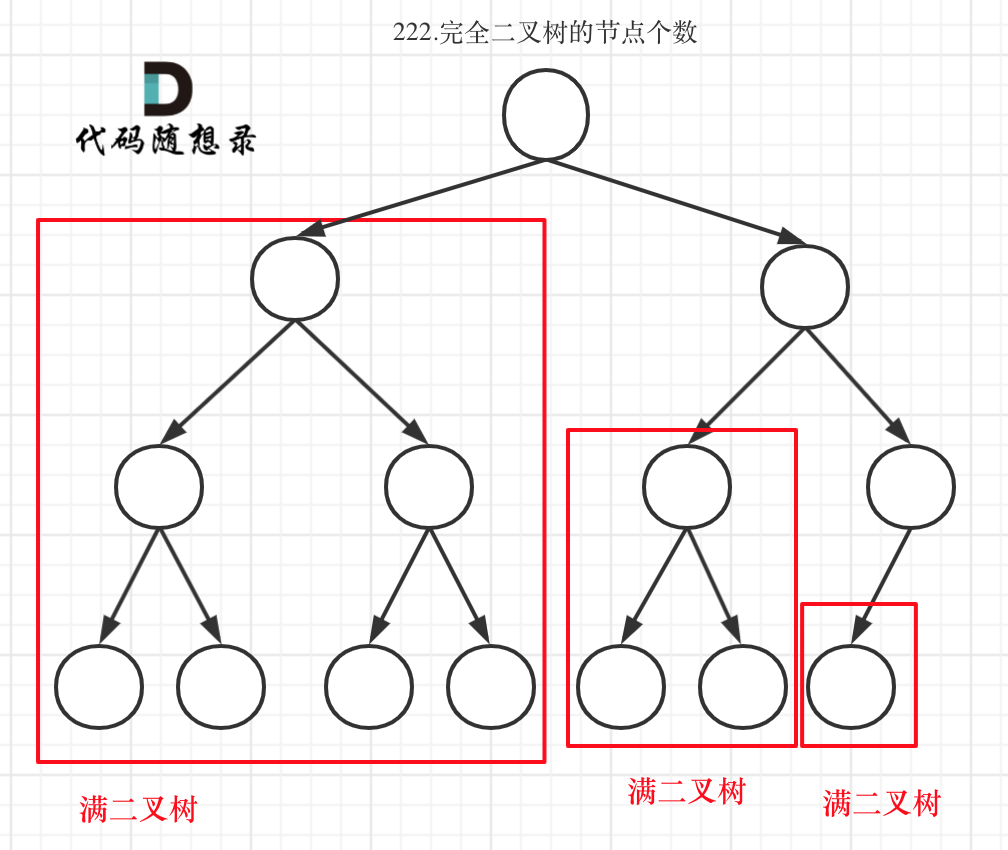
完全二叉树(二)如图: 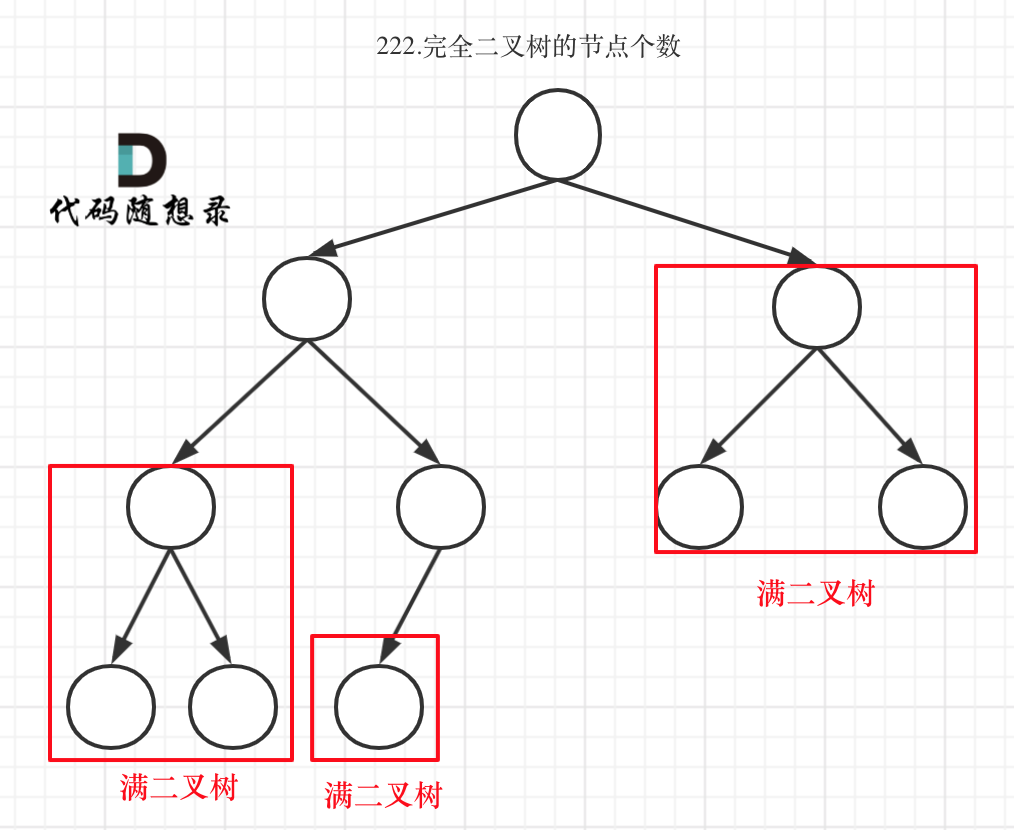
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢?
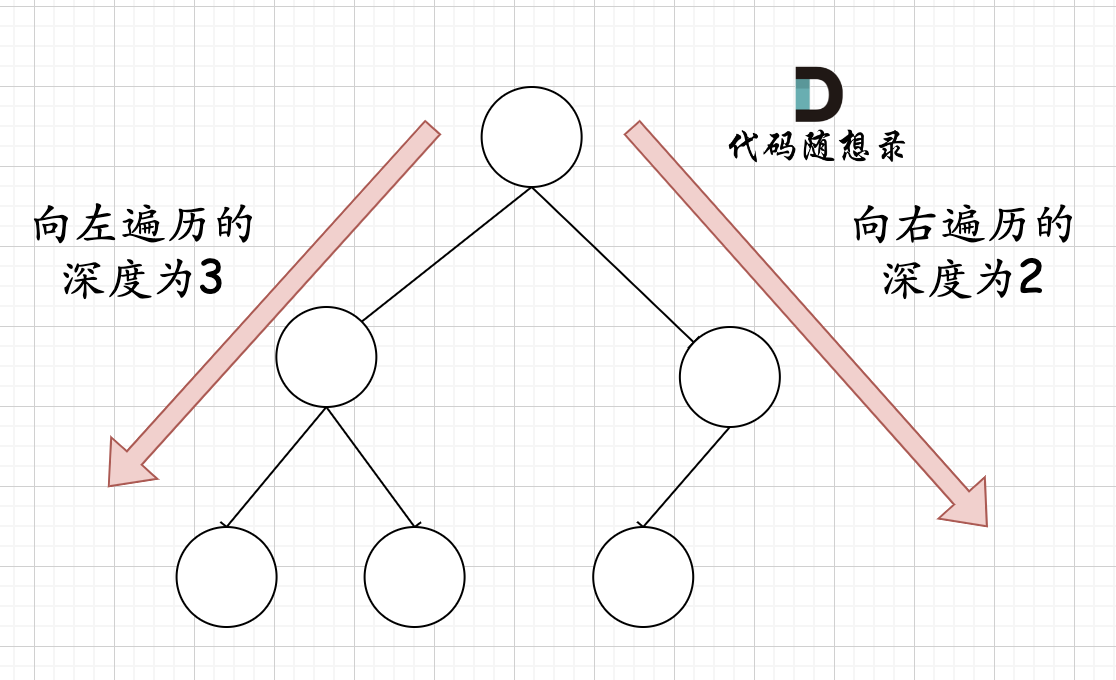
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:

在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
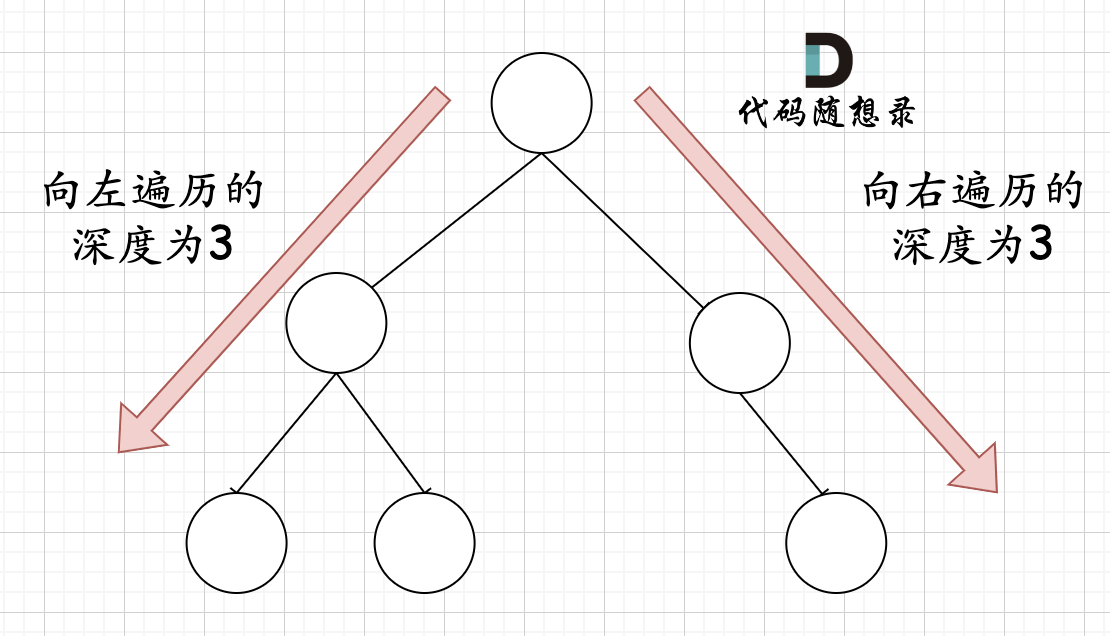
如果这么想,大家就是对 完全二叉树理解有误区了,以上这棵二叉树,它根本就不是一个完全二叉树!
判断其子树是不是满二叉树,如果是则利用公式计算这个子树(满二叉树)的节点数量,如果不是则继续递归,那么 在递归三部曲中,第二部:终止条件的写法应该是这样的:
if (root == nullptr) return 0;
// 开始根据左深度和右深度是否相同来判断该子树是不是满二叉树
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left) { // 求左子树深度left = left->left;leftDepth++;
}
while (right) { // 求右子树深度right = right->right;rightDepth++;
}
if (leftDepth == rightDepth) {return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,返回满足满二叉树的子树节点数量
}
递归三部曲,第三部,单层递归的逻辑:(可以看出使用后序遍历)
int leftTreeNum = countNodes(root->left); // 左
int rightTreeNum = countNodes(root->right); // 右
int result = leftTreeNum + rightTreeNum + 1; // 中
return result;
该部分精简之后代码为:
return countNodes(root->left) + countNodes(root->right) + 1;
最后整体C++代码如下:
class Solution {
public:int countNodes(TreeNode* root) {if (root == nullptr) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便while (left) { // 求左子树深度left = left->left;leftDepth++;}while (right) { // 求右子树深度right = right->right;rightDepth++;}if (leftDepth == rightDepth) {return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0}return countNodes(root->left) + countNodes(root->right) + 1;}
};
- 时间复杂度:O(log n × log n)
- 空间复杂度:O(log n)
这篇关于代码随想录算法训练营第十九天:二叉树go的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





