本文主要是介绍ReLU激活函数:简单之美,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原址
导语
在深度神经网络中,通常使用一种叫修正线性单元(Rectified linear unit,ReLU)作为神经元的激活函数。ReLU起源于神经科学的研究:2001年,Dayan、Abott从生物学角度模拟出了脑神经元接受信号更精确的激活模型,如下图:
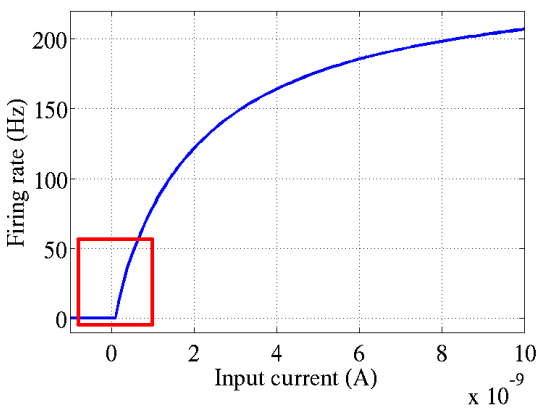
其中横轴是时间(ms),纵轴是神经元的放电速率(Firing Rate)。同年,Attwell等神经科学家通过研究大脑的能量消耗过程,推测神经元的工作方式具有稀疏性和分布性;2003年Lennie等神经科学家估测大脑同时被激活的神经元只有1~4%,这进一步表明了神经元的工作稀疏性。而对于ReLU函数而言,类似表现是如何体现的?其相比于其他线性函数(如purlin)和非线性函数(如sigmoid、双曲正切)又有何优势?下面请各位看官容我慢慢道来。
简单之美
首先,我们来看一下ReLU激活函数的形式,如下图:
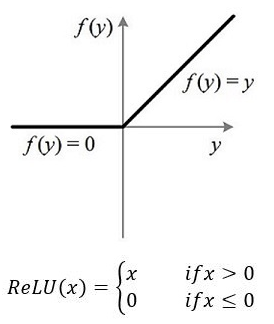
从上图不难看出,ReLU函数其实是分段线性函数,把所有的负值都变为0,而正值不变,这种操作被成为 单侧抑制 。可别小看这个简单的操作,正因为有了这单侧抑制,才使得神经网络中的神经元也具有了稀疏激活性。尤其体现在深度神经网络模型(如CNN)中,当 模型增加N层之后,理论上ReLU神经元的激活率将降低2的N次方倍 。这里或许有童鞋会问:ReLU的函数图像为什么一定要长这样?反过来,或者朝下延伸行不行?其实还不一定要长这样。只要能起到单侧抑制的作用,无论是镜面翻转还是180度翻转,最终神经元的输出也只是相当于加上了一个常数项系数,并不影响模型的训练结果。之所以这样定,或许是为了契合生物学角度,便于我们理解吧。
那么问题来了:这种稀疏性有何作用?换句话说,我们为什么需要让神经元稀疏?不妨举栗子来说明。当看名侦探柯南的时候,我们可以根据故事情节进行思考和推理,这时用到的是我们的大脑左半球;而当看蒙面唱将时,我们可以跟着歌手一起哼唱,这时用到的则是我们的右半球。左半球侧重理性思维,而右半球侧重感性思维。也就是说,当我们在进行运算或者欣赏时,都会有一部分神经元处于激活或是抑制状态,可以说是各司其职。再比如,生病了去医院看病,检查报告里面上百项指标,但跟病情相关的通常只有那么几个。与之类似,当训练一个深度分类模型的时候,和目标相关的特征往往也就那么几个,因此通过ReLU实现稀疏后的模型能够更好地挖掘相关特征,拟合训练数据。
此外,相比于其它激活函数来说,ReLU有以下优势:对于线性函数而言,ReLU的表达能力更强,尤其体现在深度网络中;而对于非线性函数而言,ReLU由于非负区间的梯度为常数,因此不存在梯度消失问题(Vanishing Gradient Problem),使得模型的收敛速度维持在一个稳定状态。这里稍微描述一下什么是梯度消失问题:当梯度小于1时,预测值与真实值之间的误差每传播一层会衰减一次,如果在深层模型中使用sigmoid作为激活函数,这种现象尤为明显,将导致模型收敛停滞不前。
这篇关于ReLU激活函数:简单之美的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





