Day 63:单调栈 LeedCode 84.柱状图中最大的矩形

本文主要是介绍Day 63:单调栈 LeedCode 84.柱状图中最大的矩形，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

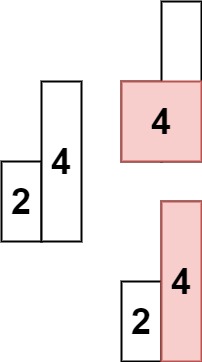
输入： heights = [2,4]
输出： 4

提示：

1 <= heights.length <=105
0 <= heights[i] <= 104

思路:

本题和接雨水有相似之处

Day62:单调栈 LeedCode503. 下一个更大元素 II 42. 接雨水-CSDN博客

1.暴力法:

最大面积的矩形的高,一定是某个柱子的高

求出以每根柱子的高为矩形的高的矩形的最大矩形面积

寻找当前柱子的左边和右边第一个小于其高度的柱子,这两个柱子之间的宽度为矩形的宽w,h为当前柱子的高,面积为w*h

代码参考:

class Solution {public int largestRectangleArea(int[] heights) {int sum=0;for(int i=0;i<heights.length;i++){int left=i;int right=i;for(;left>=0;left--){if(heights[left]<heights[i]){break;}}for(;right<heights.length;right++){if(heights[right]<heights[i]){break;}}sum=Math.max(sum,(right-left-1)*heights[i]);}return sum;}
}

暴力法时间超过限制

2.双指针法:

为了得到两边的比当前高度矮的柱子，使用了暴力法，每到一个柱子都向两边遍历一遍，这其实是有重复计算的。我们把每一个位置的左边第一个高度小于当前高度的位置记录在一个数组上（ minLeftIndex），右边第一个高度小于当前高度的位置记录在一个数组上（minRightIndex），这样就避免了重复计算。利用空间换时间

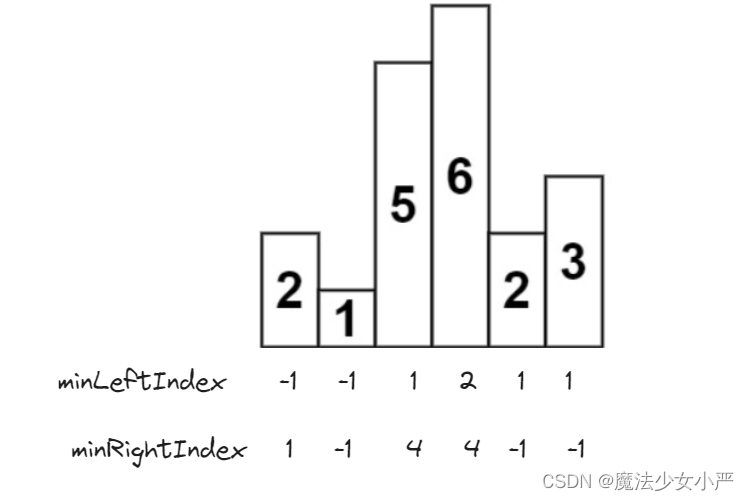
class Solution {public int largestRectangleArea(int[] heights) {int length = heights.length;int[] minLeftIndex = new int [length];int[] minRightIndex = new int [length];// 记录左边第一个小于该柱子的下标minLeftIndex[0] = -1 ;for (int i = 1; i < length; i++) {int t = i - 1;// 这里不是用if，而是不断向右寻找的过程while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];minLeftIndex[i] = t;}// 记录每个柱子右边第一个小于该柱子的下标minRightIndex[length - 1] = length;for (int i = length - 2; i >= 0; i--) {int t = i + 1;while(t < length && heights[t] >= heights[i]) t = minRightIndex[t];minRightIndex[i] = t;}// 求和int result = 0;for (int i = 0; i < length; i++) {int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);result = Math.max(sum, result);}return result;}
}

3.单调栈法

那么因为本题是要找每个柱子左右两边第一个小于该柱子的柱子，所以从栈头（元素从栈头弹出）到栈底的顺序应该是从大到小的顺序！

为什么末尾和开头要加0?

首先来说末尾为什么要加元素0？

如果数组本身就是升序的，例如[2,4,6,8]，那么入栈之后从栈头到栈底都是单调递减，一直都没有走情况一计算结果的哪一步，所以最后输出的就是0了

开头为什么要加元素0？

如果栈中只有一个元素,将栈顶弹出得到mid，栈里没有元素了，那么为了避免空栈取值，直接跳过了计算结果的逻辑。

所以我们需要在 height数组前后各加一个元素0。

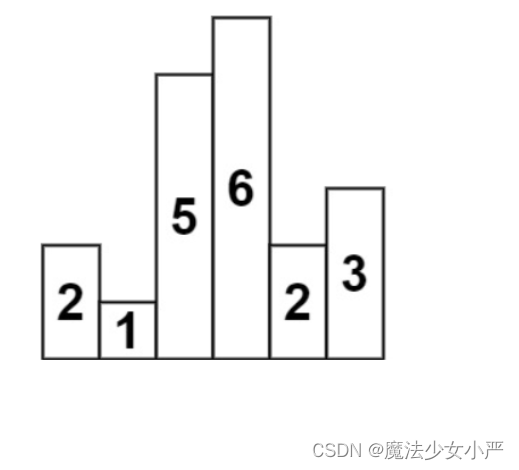
情况一：当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
将栈中比当前元素小的都出栈

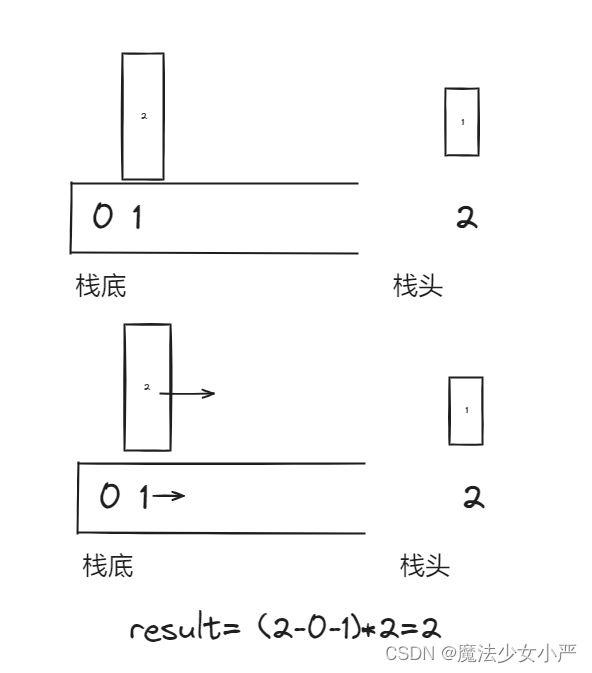
情况二：当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
直接入栈

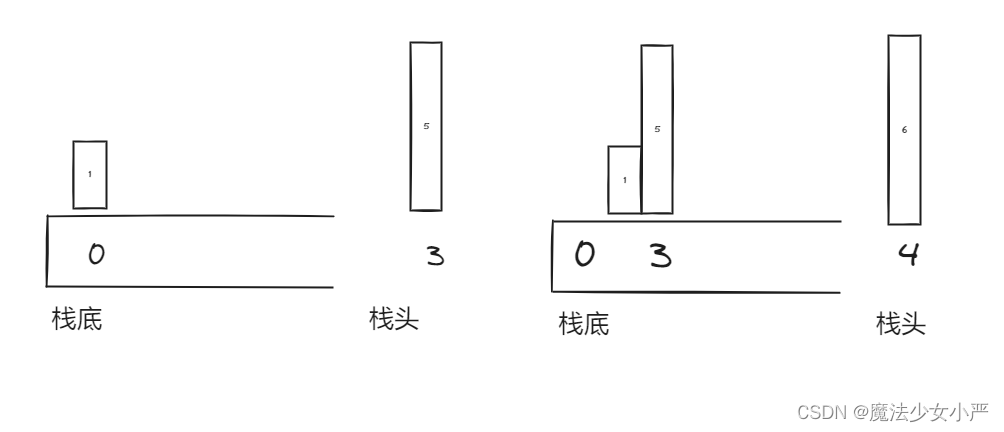
情况三：当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
将栈顶的元素更新为当前元素

图略

代码参考:

class Solution {public int largestRectangleArea(int[] heights) {int result=0;LinkedList<Integer> list=new LinkedList<>();//首尾插入0int[] newHeigths=new int[heights.length+2];System.arraycopy(heights, 0, newHeigths, 1, heights.length);newHeigths[heights.length+1]=0;list.add(0);for(int i=1;i<newHeigths.length;i++){if(newHeigths[i]>newHeigths[list.get(list.size()-1)]){list.add(i);}else if(newHeigths[i]==newHeigths[list.get(list.size()-1)]){//可以省略list.remove(list.size()-1);list.add(i);}else{while(newHeigths[i]<newHeigths[list.get(list.size()-1)]){int mid=list.get(list.size()-1);list.remove(list.size()-1);int left=list.get(list.size()-1);int right=i;int w=right-left-1;int h=newHeigths[mid];result=Math.max(result,w*h);}list.add(i);}}return result;}
}

public static void arraycopy(Object src, int srcPos, Object dest, int destPos, int length)

src:源数组;

srcPos:源数组要复制的起始位置;

dest:目的数组;

destPos:目的数组放置的起始位置;

length:复制的长度.

总结:

要解决本题就要快速找到当前位置的左边第一个高度低于当前值的位置和右边第一个高度低于当前值的位置

为什么单调栈能帮我们快速找出这两个位置?

对于栈顶元素,栈顶往栈底方向的下一个元素,是第一个小于当前值的(从栈低到栈顶递增),所以对于单调栈很容易找到左边那个位置,如果接下来即将入栈的元素小于栈顶对应的值,那这个接下来要入栈的元素不就是我们要找的那个右边的那个值吗?

建议与接雨水题目一起思考:

Day62:单调栈 LeedCode503. 下一个更大元素 II 42. 接雨水-CSDN博客