本文主要是介绍多目标灰狼算法(MOGWO):原理讲解与代码实现 Matlab代码免费获取,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
声明:文章是从本人公众号中复制而来,因此,想最新最快了解各类智能优化算法及其改进的朋友,可关注我的公众号:强盛机器学习,不定期会有很多免费代码分享~
目录
原理简介
一、Pareto最优概念
二、单目标GWO
三、多目标GWO优化机制
四、整体算法流程
代码实现
今天为大家带来一期多目标灰狼算法(MOGWO)代码,该算法由 Seyedali Mirjalili 等人于 2016 年发表在SCI一区顶刊《Expert Systems With Applications》上!

目前,MOGWO已经被广泛应用于如能源系统优化、物流路径优化、参数调优等不同场景,相比于单目标算法,多目标算法考虑的内容更多,更容易受到审稿人的青睐。
本期代码免费赠送,需要代码的小伙伴可直接拉到最后!
原理简介
一、Pareto最优概念
多目标灰狼优化算法 (Multi-objective Grey Wolf Optimizer, MOGWO)是灰狼优化算法(GWO)的多目标版本,旨在解决多准则下无法比较多目标空间中解的优劣问题,因此引入了Pareto最优解集的概念。
以最小化为例,解A对解B在某个目标函数上存在f(A)<f(B),则称解A支配解B。在解集内,找不到其他解在所有目标函数上都优于解A的解,则解A为Pareto最优解,这一类解组成的集合为Pareto最优解集,而Pareto前沿则由Pareto最优解的目标函数值组成。

二、单目标GWO
为了更好地了解MOGWO,首先介绍一下单目标GWO原理。单目标GWO通过模仿灰狼捕猎行为进行寻优,其数学模型如下:

式中:t为当前迭代次数;Xα、Xβ和Xδ为阿尔法狼、贝塔狼和德尔塔狼的位置向量;X为灰狼的位置向量;A和C是系数向量。其计算如下:

式中:a在迭代过程中线性地从2减少到0;r1和r2则是[0,1]的随机向量。
三、多目标GWO优化机制
不同于传统的单目标算法,多目标算法能够通过寻找帕累托解平衡多个相互竞争的目标。而MOGWO相比于其他多目标算法,则有两个较为明显的改进,一是引入存档机制,二是改进头狼选择方式。
第一,存档机制。外部存档Archive保存到目前为止获得Pareto最优解,在迭代中新得到的非支配解与存档中的常驻解采用以下处理方式:
(1)新个体被至少以一个存档中的常驻解支配时,新个体不被允许进入存档。
(2)新个体支配存档中的一个或多个解时,新个体进入存档,存档内被支配的解则被省略掉。
(3)如果新个体与存档内的解都不相互支配,则应将新个体加入存档。
(4)当存档已满时,运行网格机制重新安排目标空间的分割,去掉最拥挤的部分的一个解,将新解插入到最不拥挤的位置,以提高Pareto前沿的多样性。
第二,改进头狼选择方式。为选择出合适的三匹头狼(α狼、β狼、δ狼),通过轮盘赌法在Archive中最不拥挤的部分按照如下概率选择头狼:

式中:c为大于1的常数;Ni为该第i组中Pareto最优解个数。
四、整体算法流程
MOGWO的具体流程如下:
(1)设置算法的种群数量、最大迭代次数,设置外部存档Archive大小、轮盘赌法参数等。
(2)计算种群个体的目标参数值,确定支配关系,将非支配解存入Archive中。
(3)根据外部存档中的拥挤度,依据轮盘赌法确定头狼(α狼、β狼、δ狼)。
(4)利用得到的头狼更新种群个体位置并计算目标函数值。
(5)比较新的种群个体与存档中个体的支配关系,确定新的非支配解更新存档。
(6)对步骤(3)、步骤(4)和步骤(5)迭代运行,达到迭代上限停止,输出Archive解。

代码实现
MOGWO核心代码如下:
clear
clc
drawing_flag = 1;
nVar=5;%% 测试函数
fobj=@(x) ZDT3(x);%% MOGWO算法参数
lb=zeros(1,5);
ub=ones(1,5);
VarSize=[1 nVar];
GreyWolves_num=100; % 种群数量
MaxIt=50; % 迭代次数
Archive_size=100; % 存档数量%% 网格机制的参数
alpha=0.1; % Grid Inflation Parameter
nGrid=10; % Number of Grids per each Dimension
beta=4; % Leader Selection Pressure Parameter
gamma=2; % Extra (to be deleted) Repository Member Selection Pressure%% 种群初始化
GreyWolves=CreateEmptyParticle(GreyWolves_num);
for i=1:GreyWolves_numGreyWolves(i).Velocity=0;GreyWolves(i).Position=zeros(1,nVar);for j=1:nVarGreyWolves(i).Position(1,j)=unifrnd(lb(j),ub(j),1);endGreyWolves(i).Cost=fobj(GreyWolves(i).Position')';GreyWolves(i).Best.Position=GreyWolves(i).Position;GreyWolves(i).Best.Cost=GreyWolves(i).Cost;
end%% 确定支配关系
GreyWolves=DetermineDomination(GreyWolves);%% 非支配解存档
Archive=GetNonDominatedParticles(GreyWolves);%% 网格机制
Archive_costs=GetCosts(Archive);
G=CreateHypercubes(Archive_costs,nGrid,alpha);for i=1:numel(Archive)[Archive(i).GridIndex Archive(i).GridSubIndex]=GetGridIndex(Archive(i),G);
end%% 主程序迭代
for it=1:MaxIta=2-it*((2)/MaxIt);for i=1:GreyWolves_numclear rep2clear rep3% Choose the alpha, beta, and delta grey wolvesDelta=SelectLeader(Archive,beta);Beta=SelectLeader(Archive,beta);Alpha=SelectLeader(Archive,beta);% If there are less than three solutions in the least crowded% hypercube, the second least crowded hypercube is also found% to choose other leaders from.if size(Archive,1)>1counter=0;for newi=1:size(Archive,1)if sum(Delta.Position~=Archive(newi).Position)~=0counter=counter+1;rep2(counter,1)=Archive(newi);endendBeta=SelectLeader(rep2,beta);end% This scenario is the same if the second least crowded hypercube% has one solution, so the delta leader should be chosen from the% third least crowded hypercube.if size(Archive,1)>2counter=0;for newi=1:size(rep2,1)if sum(Beta.Position~=rep2(newi).Position)~=0counter=counter+1;rep3(counter,1)=rep2(newi);endendAlpha=SelectLeader(rep3,beta);end% Eq.(3.4) in the paperc=2.*rand(1, nVar);% Eq.(3.1) in the paperD=abs(c.*Delta.Position-GreyWolves(i).Position);% Eq.(3.3) in the paperA=2.*a.*rand(1, nVar)-a;% Eq.(3.8) in the paperX1=Delta.Position-A.*abs(D);% Eq.(3.4) in the paperc=2.*rand(1, nVar);% Eq.(3.1) in the paperD=abs(c.*Beta.Position-GreyWolves(i).Position);% Eq.(3.3) in the paperA=2.*a.*rand()-a;% Eq.(3.9) in the paperX2=Beta.Position-A.*abs(D);% Eq.(3.4) in the paperc=2.*rand(1, nVar);% Eq.(3.1) in the paperD=abs(c.*Alpha.Position-GreyWolves(i).Position);% Eq.(3.3) in the paperA=2.*a.*rand()-a;% Eq.(3.10) in the paperX3=Alpha.Position-A.*abs(D);% Eq.(3.11) in the paperGreyWolves(i).Position=(X1+X2+X3)./3;% Boundary checkingGreyWolves(i).Position=min(max(GreyWolves(i).Position,lb),ub);GreyWolves(i).Cost=fobj(GreyWolves(i).Position')';endGreyWolves=DetermineDomination(GreyWolves);non_dominated_wolves=GetNonDominatedParticles(GreyWolves);Archive=[Archivenon_dominated_wolves];Archive=DetermineDomination(Archive);Archive=GetNonDominatedParticles(Archive);for i=1:numel(Archive)[Archive(i).GridIndex Archive(i).GridSubIndex]=GetGridIndex(Archive(i),G);endif numel(Archive)>Archive_sizeEXTRA=numel(Archive)-Archive_size;Archive=DeleteFromRep(Archive,EXTRA,gamma);Archive_costs=GetCosts(Archive);G=CreateHypercubes(Archive_costs,nGrid,alpha);enddisp(['In iteration ' num2str(it) ': Number of solutions in the archive = ' num2str(numel(Archive))]);save results% Resultscosts=GetCosts(GreyWolves);Archive_costs=GetCosts(Archive);if drawing_flag==1hold offplot(costs(1,:),costs(2,:),'k.');hold onplot(Archive_costs(1,:),Archive_costs(2,:),'r*');legend('灰狼种群','非支配解');set(gcf,'color','w')drawnowendend
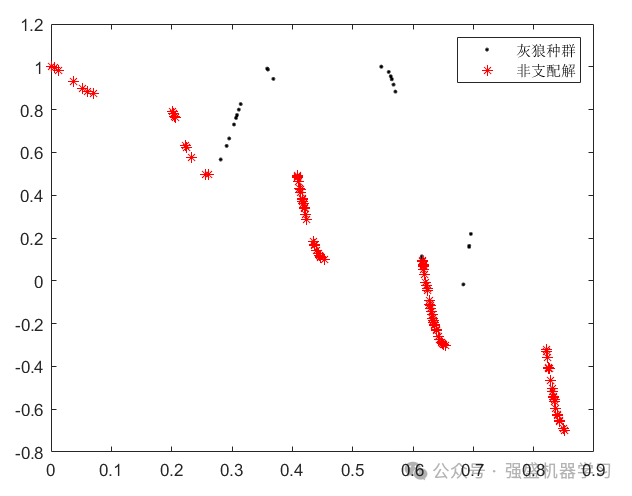
代码里提供了四种多目标函数,分别为ZDT1、ZDT2、ZDT3、ZDT4,大家可以自行切换,以ZDT3为例:

这是迭代过程图,图中可以很清晰的显示灰狼种群与各非支配解,在迭代完成后选择需要的非支配解即可。
其中有部分函数封装为了子函数,文章中无法全部放下。因此,需要完整代码的小伙伴只需点击下方小卡片,后台回复关键词,不区分大小写:
MOGWO
若有其他更多代码需求或免费代码,可查看链接:更多代码链接
这篇关于多目标灰狼算法(MOGWO):原理讲解与代码实现 Matlab代码免费获取的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






