本文主要是介绍mmm含树 查询点的提示,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这是今年GDKOI的一题:有一棵树,开始时所有结点的值都是0。有多个操作,每个操作有两种:
1.对某个点增加w,设dis(i,j)为点i到点j的最短距离,那么某个结点增加w时,对于任意一个结点j,它的值会增加w + dis(i,j)。
2.询问某点的值。
w可以忽略,因为整棵树都要加上w,只要记下所有w的和就可以了,输出答案时再加上。这题的突破口就是只需要求一个点的值,这就取决于其他发生变化的点对该点的影响。这里先结合一个样例,说明一些变量:
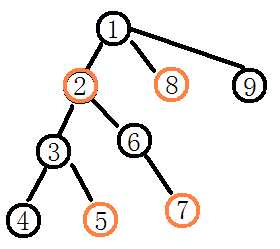
如图:点2,5,7,8被修改过(忽略了w)。
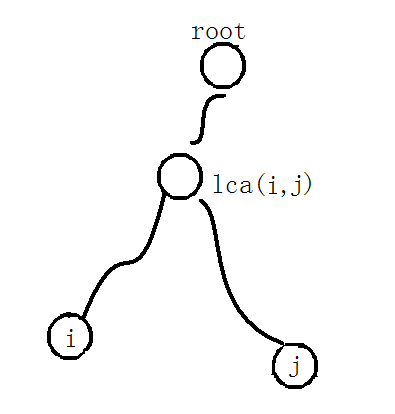
dis(i,j):点i到点j的最短距离。
lca(i,j):点i和点j的最近公共祖先。
dep(i):点i到根结点的距离,dep(6)= 2,dep(5)= 3。
cnt(i):以i为根的子树中的点,被修改过的次数,cnt(3)= 1,cnt(2)= 3。
deps(i):以i为根的子树中的被修改过的点的dep和,deps(2) = dep(2)+ dep(5)+ dep(7) = 1 + 3 + 3 = 7。
首先,要求任意两点i,j的距离,用dis(i,j)来表示是不好的,因为这没有内在的关系。这个可以表示成dep(i)+ dep(j)- 2 * dep(lca(i,j))。画个图就知道了。
如样例,有一个询问,询问3的值,那么它等于:
dep(3)* cnt(3) + deps(3) - 2 * dep(3)* cnt(3)
+dep(3)* (cnt(2)- cnt(3)) + (deps(2)- deps(3)) - 2 * dep(2)*(cnt(2)- cnt(3))
+dep(3)* (cnt(1)- cnt(2)) + (deps(1)- deps(2)) - 2 * dep(1)*(cnt(1)- cnt(2))
可以发现,有很多值是可以约去的,还有dep(2)= dep(3)- 1,dep(1)= dep(3)- 2,化简得:
dep(3) * cnt(1) + deps(1) - 2 * (cnt(3) + cnt(2))。
再可以由此推到普遍:
询问点u:dep(u) * cnt(1) + deps(1) - 2 * (cnt(u) + cnt(u的父亲) + cnt(u的父亲的父亲) + … + cnt(根的儿子))。注意不要加到根。
如此看来,我们需要的只是求cnt的和。这个可以用树链剖分来统计。
对于这些改一些,问一些的题目,不要局限于维护答案的值,可以通过维护其他的信息,以便于求答案。
贴个代码:
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;inline int getInt()
{int res = 0;char ch;for (ch = '#'; ch < '0' || ch > '9'; ch = getchar());for (; ch >= '0' && ch <= '9'; ch = getchar())res = res * 10 + (int) ch - 48;return res;
}const int N = 100007;int n;
int from[N], to[N << 1], next[N << 1], nedge;void Insert(int a, int b)
{to[nedge] = b;next[nedge] = from[a];from[a] = nedge ++;
}void Init()
{n = getInt();memset(from, -1, sizeof(from));nedge = 0;for (int i = 0; i + 1 < n; i ++){int a = getInt() - 1, b = getInt() - 1;Insert(a, b);Insert(b, a);}
}int Q[N];
int father[N], size[N], dep[N];
int npath, top[N], len[N], belong[N], idx[N];void Split()
{int lo = 0, hi = 0;npath = 0;Q[0] = 0;father[0] = -1;dep[0] = 0;while (lo <= hi){int u = Q[lo ++];for (int e = from[u]; e != -1; e = next[e]){int v = to[e];if (v != father[u]){Q[++ hi] = v;father[v] = u;dep[v] = dep[u] + 1;}}}for (int i = n - 1; i >= 0; i --){int u = Q[i], p = -1;size[u] = 1;for (int e = from[u]; e != -1; e = next[e]){int v = to[e];if (v != father[u]){size[u] += size[v];if (p == -1 || size[v] > size[p])p = v;}}if (p == -1){belong[u] = npath;top[npath] = u;idx[u] = 0;len[npath ++] = 1;}else {int x = belong[p];top[x] = u;idx[u] = len[x] ++;belong[u] = x;}}
}int nnode;
struct Node
{Node *lch, *rch;int lo, hi;ll sum, val;inline int mi(){return (lo + hi) >> 1;}inline int size(){return hi - lo;}
}node[N << 1], *tree[N];void Build(Node *p, int lo, int hi)
{p -> lo = lo;p -> hi = hi;p -> sum = p -> val = 0LL;if (lo + 1 == hi)p -> lch = p -> rch = NULL;else {int mi = p -> mi();p -> lch = &node[nnode ++];p -> rch = &node[nnode ++];Build(p -> lch, lo, mi);Build(p -> rch, mi, hi);}
}inline void Down(Node *p)
{p -> lch -> val += p -> val;p -> rch -> val += p -> val;p -> lch -> sum += p -> lch -> size() * p -> val;p -> rch -> sum += p -> rch -> size() * p -> val;p -> val = 0LL;
}void Modify(Node *p, int le, int ri)
{if (le <= p -> lo && ri >= p -> hi){p -> val ++;p -> sum += p -> size();}else {if (p -> val) Down(p);int mi = p -> mi();if (le < mi) Modify(p -> lch, le, ri);if (ri > mi) Modify(p -> rch, le, ri);p -> sum = p -> lch -> sum + p -> rch -> sum;}
}ll Ask(Node *p, int le, int ri)
{if (le <= p -> lo && ri >= p -> hi)return p -> sum;else {if (p -> val) Down(p);int mi = p -> mi();ll ret = 0LL;if (le < mi) ret += Ask(p -> lch, le, ri);if (ri > mi) ret += Ask(p -> rch, le, ri);return ret;}
}void Prepare()
{nnode = 0;for (int i = 0; i < npath; i ++){tree[i] = &node[nnode ++];Build(tree[i], 0, len[i]);}
}ll Find(int a, bool isask)
{int x = belong[a];ll ret = 0LL;while (x != belong[0]){if (isask) ret += Ask(tree[x], idx[a], len[x]);else Modify(tree[x], idx[a], len[x]);a = father[top[x]];x = belong[a];}if (a != 0)if (isask) ret += Ask(tree[x], idx[a], idx[0]);else Modify(tree[x], idx[a], len[x]);return ret;
}void Solve()
{ll w = 0LL, cnt = 0LL;for (int T = getInt(); T; T --)if (getInt() == 0){int u = getInt() - 1;Find(u, false);w += getInt();w += (ll) dep[u];cnt ++;}else {int u = getInt() - 1;ll res = - 2 * Find(u, true);res += w + cnt * dep[u];printf("%I64d\n", res);}
}int main()
{freopen("mmmfunc.in", "r", stdin);freopen("mmmfunc.out", "w", stdout);for (int T = getInt(); T; T --){Init();Split();Prepare();Solve();}return 0;
}
这篇关于mmm含树 查询点的提示的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!