力扣：221. 最大正方形

本文主要是介绍力扣：221. 最大正方形，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

221. 最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

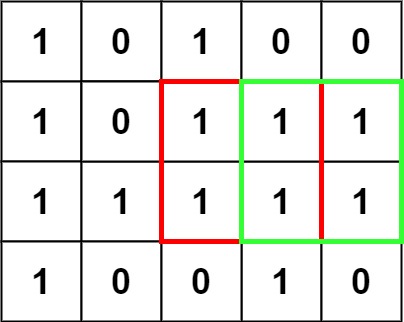
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

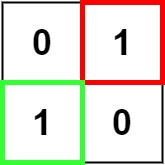
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

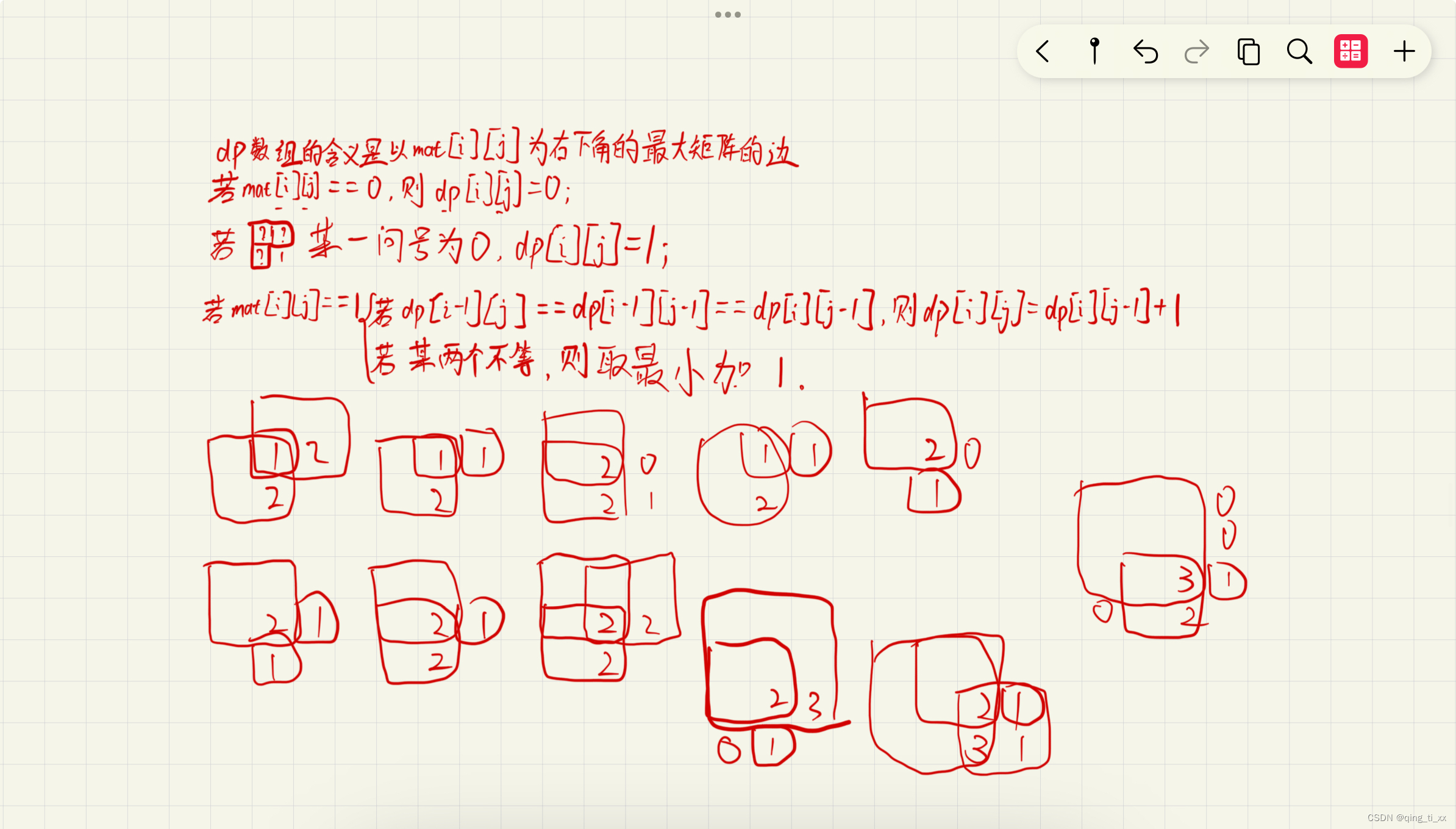
class Solution {public int maximalSquare(char[][] mat) {int m = mat.length;int n = mat[0].length;int[][] dp = new int[m][n];int max = 0;//max为0for(int i = 0;i < m;i++){dp[i][0] = mat[i][0]=='1'?1:0;//检查是否为0max = Math.max(max,dp[i][0]);//记录最大的边长}for(int i = 0;i < n;i++){dp[0][i] = mat[0][i]=='1'?1:0;max = Math.max(max,dp[0][i]);}if(m==1||n==1)return max;for(int i = 1;i < m;i++){for(int j = 1;j < n;j++){if(mat[i][j]=='0'){dp[i][j] = 0;}else{if(dp[i-1][j]==0||dp[i-1][j-1]==0||dp[i][j-1]==0){dp[i][j] = 1;}else{dp[i][j] = Math.min(dp[i-1][j],Math.min(dp[i-1][j-1],dp[i][j-1]))+1;}}max = Math.max(max,dp[i][j]);//记录最大值}}return max*max;//计算面积返回}
}

这篇关于力扣：221. 最大正方形的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---