本文主要是介绍二分+计数,CF1569D Inconvenient Pairs,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
二、解题报告
1、思路分析
2、复杂度
3、代码详解
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
Problem - 1569D - Codeforces
二、解题报告
1、思路分析
我们考虑路径距离等于曼哈顿距离的点对长什么样子?
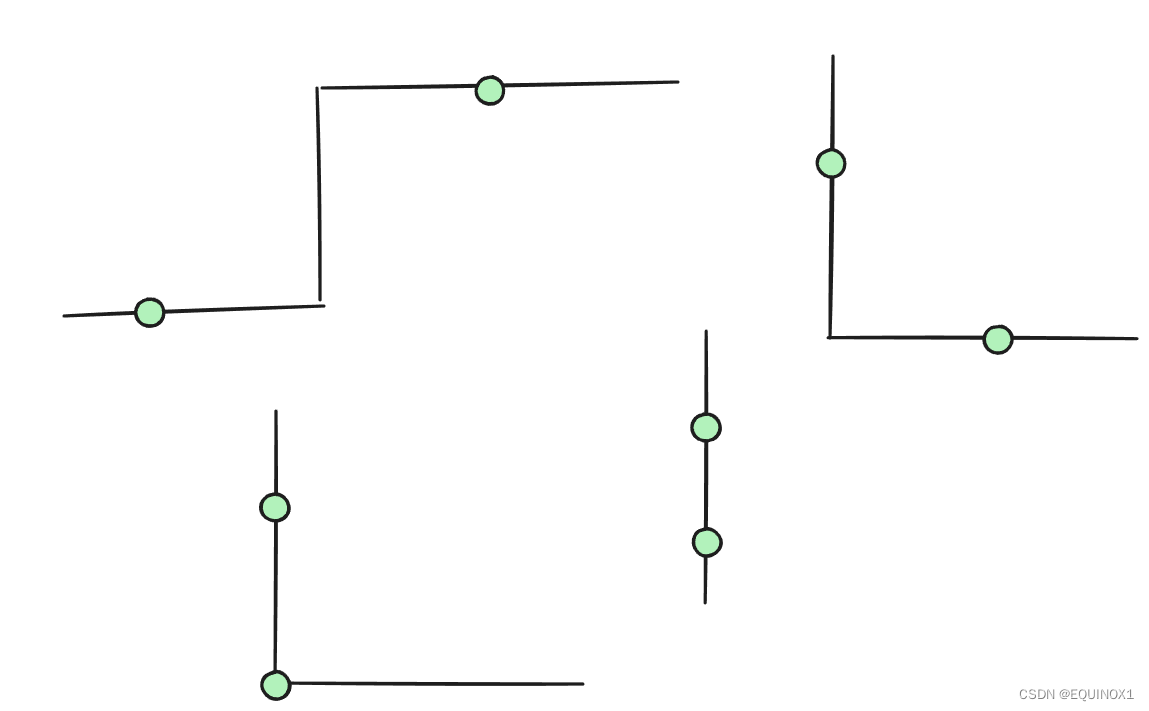
如果某点在交点上,那么它到任意点的距离都是曼哈顿距离,我们直接删除这个点
我们发现距离不是曼哈顿距离的点对,它们所处的线段一定平行且不重合
那么我们记录每组平行线段上点的数目ti,以及每个线段上点的数目kij
答案就是 Σ(ti - 1) * ti / 2 - Σ(kij - 1) * kij / 2
具体统计每个点处于哪个竖直线段还是水平线段时,由于每个线段的左(下)端点都不同,我们以左(下)端点来区分每个(组)线段即可
具体看代码
2、复杂度
时间复杂度: O(n + m + k(logn + logm))空间复杂度:O(n + m)
3、代码详解
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int xs[N], ys[N];void solve(){int n, m, k;cin >> n >> m >> k;unordered_map<int, int> cntx, cnty;unordered_map<int, unordered_map<int, int>> cntxy, cntyx;for(int i = 0; i < n; i ++) cin >> xs[i];for(int i = 0; i < m; i ++) cin >> ys[i];for(int i = 0, x, y; i < k; i ++){cin >> x >> y;int lx = lower_bound(xs, xs + n, x) - xs, ly = lower_bound(ys, ys + m, y) - ys;if(xs[lx] == x && ys[ly] == y) continue; //删掉if(xs[lx] == x){ //verticalcnty[ly] ++;cntxy[lx][ly] ++;} else{ //horizontalcntx[lx] ++;cntyx[ly][lx] ++; }}int res = 0;for(int i = 0; i < n; i ++){int t = cntx[i];res += t * (t - 1) / 2;for(auto& p : cntxy[i]){t = p.second;res -= t * (t - 1) / 2;}}for(int i = 0; i < m; i ++){int t = cnty[i];res += t * (t - 1) / 2;for(auto& p : cntyx[i]){t = p.second;res -= t * (t - 1) / 2;}} cout << res << '\n';
}signed main(){ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int _ = 1;cin >> _;while(_ --)solve(); return 0;
}这篇关于二分+计数,CF1569D Inconvenient Pairs的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





