【论文阅读】Sparse is Enough in Scaling Transformers

本文主要是介绍【论文阅读】Sparse is Enough in Scaling Transformers，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

论文地址

1、论文

---

摘要

大型变压器模型在许多任务上都取得了令人印象深刻的结果，但训练甚至微调的费用很高，而且解码速度太慢，以至于它们的使用和研究变得遥不可及。我们通过利用稀疏性来解决这个问题。我们研究了变压器中所有层的稀疏变体，并提出了缩放变压器，这是下一代变压器模型系列，它使用稀疏层来有效地扩展，并在我们扩展模型大小时比标准 Trans- former 更快地执行非批处理解码。令人惊讶的是，稀疏层足以获得与具有相同参数数的标准变压器相同的困惑度。我们还集成了先前的稀疏性方法来吸引注意力，即使在内存有限的情况下也能对长序列进行快速推理。这导致性能可与最先进的长文本摘要相媲美。

1 介绍

近年来，由于基于Transformer架构的大型神经网络，自然语言处理领域有了显着的进步。最初的Transformer[42]在机器翻译方面取得了显著的进步。BERT [7] 超越了之前所有关于问答、语言推理和其他 NLP 任务的方法，紧随其后的是一系列模型，如 T5 [30]，进一步改善了这些结果。GPT 系列模型 [29， 3] 将语言生成提升到GPT-2 被邀请为《经济学人》撰写短文的程度，GPT-3 创建了与人类撰写的文章几乎没有区别的整篇文章。

这种进步的好处被这种模型产生的巨大成本所削弱。Strubell等人[36]估计，训练一个基础BERT模型的成本为4000-12000美元，排放的二氧化碳相当于一名乘客在4小时飞行中所占的份额，后来Patterson等人[27]估计训练GPT-3的tCO2e（公吨二氧化碳当量）排放量是SF-NY往返飞行的三倍。数据和服务成本也令人望而却步：例如，BERT的一次训练运行处理128B个令牌，据报道，谷歌翻译1每天提供超过143B个单词。

随着这些模型的日益普及和规模，使它们有效扩展变得越来越有价值。在这项工作中，我们提出了具有单独的稀疏机制的缩放转换器，用于查询、键、值和输出层（简称 QKV 层），并将其与稀疏前馈块相结合，以获得完全稀疏的转换器架构。

量化推理的计算复杂度在 Transformer 模型中，回忆一下 Transformer 解码器块的架构。它由三部分组成：一个掩蔽的自我注意层，一个编码器-解码器注意层和一个前馈块。这些层的大小由 dmodel 和 dff 参数化。 base BERT模型设置dmodel = 768，large BERT有dmodel = 1024，最大GPT-2 的 dmodel = 1600，GPT-3 达到 dmodel = 12288。对于 BERT 和 GPT 模型，作者使用 dff = 4 dmodel。在解码 token时，自注意力层需要激活四个大小为 dmodel × dmodel 的矩阵：一个用于输入到注意力的查询、键和值，一个用于合并输出。在编码器-解码器注意力中，键和值可能已经被缓存，因此只有两个大小为 dmodel × dmodel 的矩阵被激活。前馈块由两个大小为 dmodel × dff 的矩阵组成，忽略了偏差的小额外贡献。总和为：

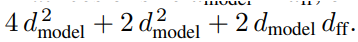
这个总和既描述了模型 modela 单个块的可训练权重的数量，也很好地近似了解码单个标记所需的浮点运算的数量，注意力操作除外（稍后讨论）。 dmodel 中的复杂度是二次的；例如，随着 dmodel 从基础 BERT 到 GPT-3 增加 16 倍，单个块的复杂度增加了 256 倍。

相比之下，Scaling Transformers 在 QKV 层模型模型中仅使用

个参数，产生的结果为与基线（完全密集）Transformer 一样好，具有相同数量的参数和复杂性：

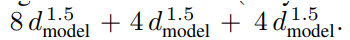
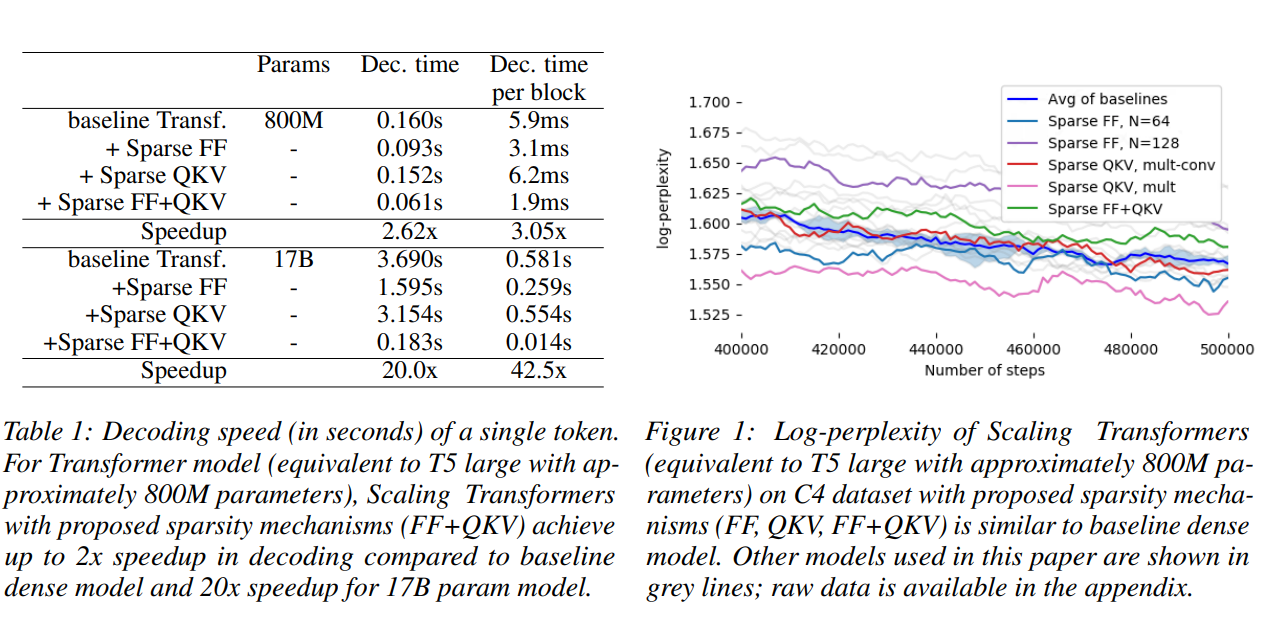
我们感到惊讶的是，完全稀疏的 Scaling 模型模型 modelTransformers 确实足以匹配大型 C4 数据集 [30] 上的基线 Transformer 的结果（图 1）。复杂性的提高不仅渐近地保持不变，而且对于具有 800M 参数的模型，已经在挂钟解码时间上产生了超过 2.6 倍的加速，对于具有 17B 参数的模型，产生了 20 倍的改进，如表 1 所示。

为了验证缩放变压器可以为了与其他 Transformer 对实际任务的改进一起使用，我们创建了 Terraformer——一种使用可逆层来提高内存效率和稀疏注意力来处理长序列的 Transformer 模型。我们在 C4 数据集上预训练 Terraformer，并针对总结 arxiv 文章的挑战性任务对其进行微调。 Terraformer 产生的结果可与最先进的 BigBird-Pegasus 相媲美，而无需在预训练中使用 Pegasus 损失（表 5）。

2 相关工作

如上一节所述，大型变压器模型带来了性能的显着改进，如 GPT-3 [3， 17] 或 T5 [44， 30] 等模型所示。训练和推理在数千亿个参数的规模上会产生很高的计算成本。许多技术提高了变压器模型的效率，Gupta和Agrawal [11]将它们分为几类，包括修剪，知识蒸馏，量化，参数共享，有效注意力和高效前馈。

模型压缩。模型修剪

[24， 2] 通过在训练后或训练期间删除不需要的权重来使矩阵更小，但是，稀疏矩阵的计算复杂性的提高通常会这样做不会导致实际硬件上的推理加速 [9]。基于结构化修剪的方法 [47、22、43] 通过利用 CPU 和 GPU 架构中硬件的稀疏性来应对这一挑战 [1]。我们的论文不同于修剪方法，因为它依赖于动态稀疏性，其中前馈层仅为每个标记加载层中的一部分权重。我们的方法是对模型量化研究 [35、38、28] 的补充，后者使用更少的位来进行权重。

模型蒸馏。

用于移动推理 [13、39] 的几种自然语言模型依靠蒸馏 [32] 来加速预训练大型模型的推理。例如，[18] 预训练一个大型模型并使用知识蒸馏和修剪来获得超过 10 倍的推理速度。我们的方法不是提取大型模型，而是通过减少从模型加载到内存中的权重数量来加速推理。

稀疏注意力。

稀疏的基于注意力的方法通过合并额外的组合机制（如 [40] 中）或选择该层关注的标记子集来提高注意力层的效率，特别是对于长序列 [31, 5, 19, 37, 15] , 4] 或其他方法 [12]。我们的工作是对这些稀疏注意力方法的补充，并在其中重用了 SOTA 的进步。注意层中的推理加速也使用瓶颈层 [39] 或分组卷积 [13]。我们的工作超越了分组卷积方法的想法，因为每个注意力头仅限于使用嵌入的固定部分，而我们的工作能够置换嵌入以提高模型质量；详见第 3.2 节。

张量分解。

上面讨论的方法显着提高了 Transformer 的速度和对长序列的处理，但是它们都没有解决基本的缩放问题：即使我们提炼成一个更小的模型，量化它并修剪一定比例的权重，复杂性仍然随着 dmodel 呈二次方增长.最后一种方法确实解决了这个缩放问题，在 [11] 中称为张量分解。不幸的是，正如那里的作者所指出的那样，该方法在处理大型输入和输出嵌入矩阵时最有效，并且如果在解码器块内使用，往往会产生比非结构化模型更低的性能。

稀疏前馈。

专家方法的混合已被证明可以在训练 [33、21、34] 中实现计算效率，扩展到一万亿个参数 [8]。关键思想是将 dff 大小的维度划分为多个部分（称为专家）并且每个标记仅检索一个部分，这将前馈块的复杂性从 2dmodeldff 降低到 2dmodeldff/nexperts。这些加速主要以训练速度来衡量，该方法侧重于前馈块。与之前的方法相比，我们训练了一个完整的权重矩阵，然后在解码过程中只为每个输入令牌激活它的特定部分；请参阅第 3.1 节。

3 Sparse is Enough

我们研究了如何稀疏化 Transformer 模型的每个部分——否则非稀疏部分支配解码时间并成为瓶颈。这意味着我们需要前馈块的稀疏等效项，关注的密集 Q、K、V 和输出层，以及 softmax 和损失之前的最终密集层。

3.1 稀疏前馈层

在基线 Transformer 中，解码速度由前馈块的执行成本。回想一下，这个块由两个全连接（密集）层组成，中间有 ReLU 非线性。这两层之间的激活向量维数通常用 dff 表示，通常比其他地方的激活维数 (dmodel) 大 4 或 8 倍。

我们利用前馈块的结构对其进行稀疏化。一个主要的观察结果是中间的 ReLU 产生了很多 zeros（2）。我们在这个中间激活向量上施加了一个固定结构：N 的每个块中只有一个浮点数被允许为非零。现有技术从权重矩阵中修剪权重或块，并且可以称为静态稀疏性。我们提出的技术将训练一个完整的权重矩阵，但在解码期间只为每个输入标记激活它的特定部分。我们称此为动态稀疏性，因为模型仅动态选择其参数的一小部分，并且选择对于每个标记都是独立的。

我们训练一个控制器来确定每个块中的哪个激活可以是非零的；其余的将被设置为零。这可以表示为

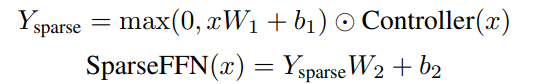
其中 ⊙ 是逐元素乘法。请注意，Ysparse 中的每个激活对应于 W1 中的单个列和 W2 中的单个行。因此，如果我们首先计算 Controller(x) 输出，则不必使用 W1 中的任何列或 W2 中对应于控制器设置为零的激活的任何行。这允许更快的解码，因为我们只需要处理 W1 中的 N 列和 W2 中的行中的 1 个（参见图 2(a)）。

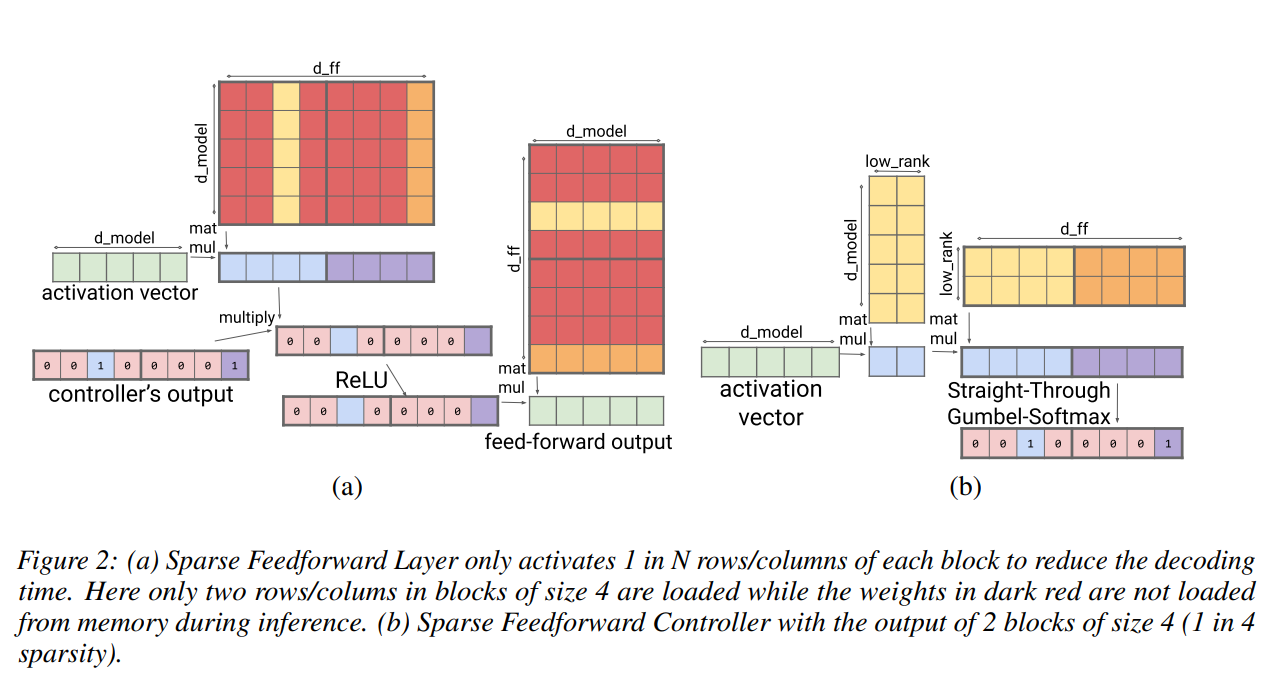
为了设计计算成本低的控制器，我们使用低秩投影输入瓶颈致密层。图 2(b) 说明了产生如下输出的控制器

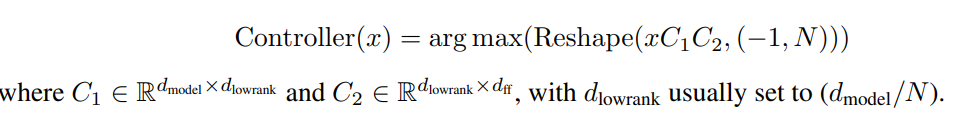
其中 C1 ∈ Rdmodel ×dlowrank 和 C2 ∈ Rdlowrank ×dff ，通常设置 dlowrank到 (dmodel /N )。

在推理期间，控制器使用离散的 argmax 函数，但在训练期间，模型使用 softmax 来计算分布并从中采样。该模型使用 Gumbel-Softmax 技巧进行离散化，学习选择非零行/列。为了确定每个块中的活动行/列，我们使用 Gumbel-Softmax 技巧 [25] 重新参数化伯努利分布的采样。我们不是使用每个块中的 logits 直接采样二进制值，而是将来自 Gumbel 分布的独立噪声添加到每个 logits，然后选择具有最高 logit（即 argmax）的二进制值作为样本 z。 argmax 操作不可微分，但可以用具有退火温度的 softmax 来近似。因此，在正向传播中，我们使用 argmax 为每个块获得一个二进制单热向量，而在反向传播中，我们用 softmax 对其进行近似。这种方法被称为直通 Gumbel-Softmax 估计器 [14].

Ablations.
我们研究了稀疏 FF 对等同于具有不同稀疏度的 T5-large 模型的影响，其中 dmodel = 1024，dff = 4096 和 16 个注意力头。当我们将稀疏度级别设置为 N（例如 N = 64）时，每个大小为 N 的块都会激活一个非零值以进行推理。在训练期间，控制器使用 dlowrank = 64 的瓶颈层和 Gumbel softmax 估计器的温度设置为 0.1。为了提高训练稳定性，前向传递中的控制器将使用 argmax 的输出，它是每个块的二元单热向量，概率为 30%，否则使用 softmax 的输出。表 2 和图 3 显示了该模型在前馈层中具有不同稀疏程度的困惑度和解码时间。随着稀疏度水平从 0 增加到 128，我们观察到解码时间显着减少，而 N = 64 稀疏度的模型的负对数困惑度与基线相当。

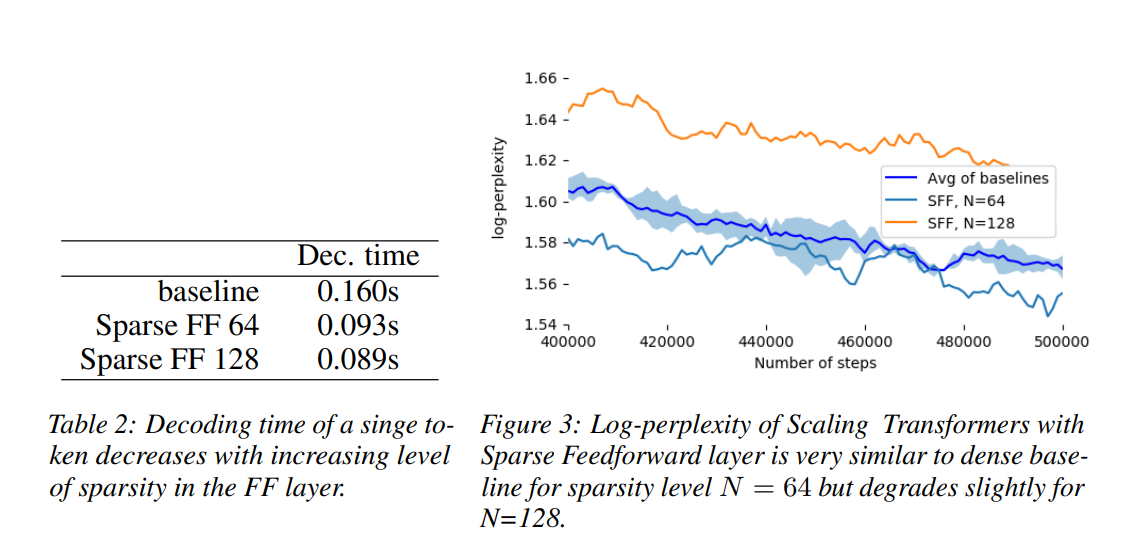
我们还用专家混合物 [33] 风格的稀疏性检查了前馈块的性能。正如预期的那样，这种技术实现了与稀疏FF相当的解码时间 - 0.11s而不是0.09s - 但由于缺乏粒度，它达到了1.64的对数困惑度，比我们的方法和密集基线都差。

3.2 稀疏 QKV 层

具有稀疏前馈块的模型的解码速度接下来由查询、键、值和输出计算决定——注意中的密集层，我们共同称为 QKV 层。这些密集层中的每一个都有 d 2 个参数和计算成本。不幸的是，QKV 层模型没有 ReLU，因此上面用于稀疏前馈块的方法在这里不可行。为了使 QKV 层稀疏，我们将层的维度 dmodel 细分为大小为 M = dmodel/S 的 S 个模块，类似于将激活向量拆分为多个头。这些模块可以使用权重更少、计算速度更快的卷积层进行处理。然而，使用 näıve 设计每个模块（和相应的注意力头）只能访问给定标记嵌入的一小部分。为了缓解这种情况，我们开发了一个乘法层，它可以表示任意排列，并且比密集层具有更少的参数和更少的计算时间。该乘法层恰好插入卷积层之前，让每个头访问嵌入的任何部分（参见图 4(a)）。该解决方案产生了性能良好的模型，这些模型也可以快速解码。

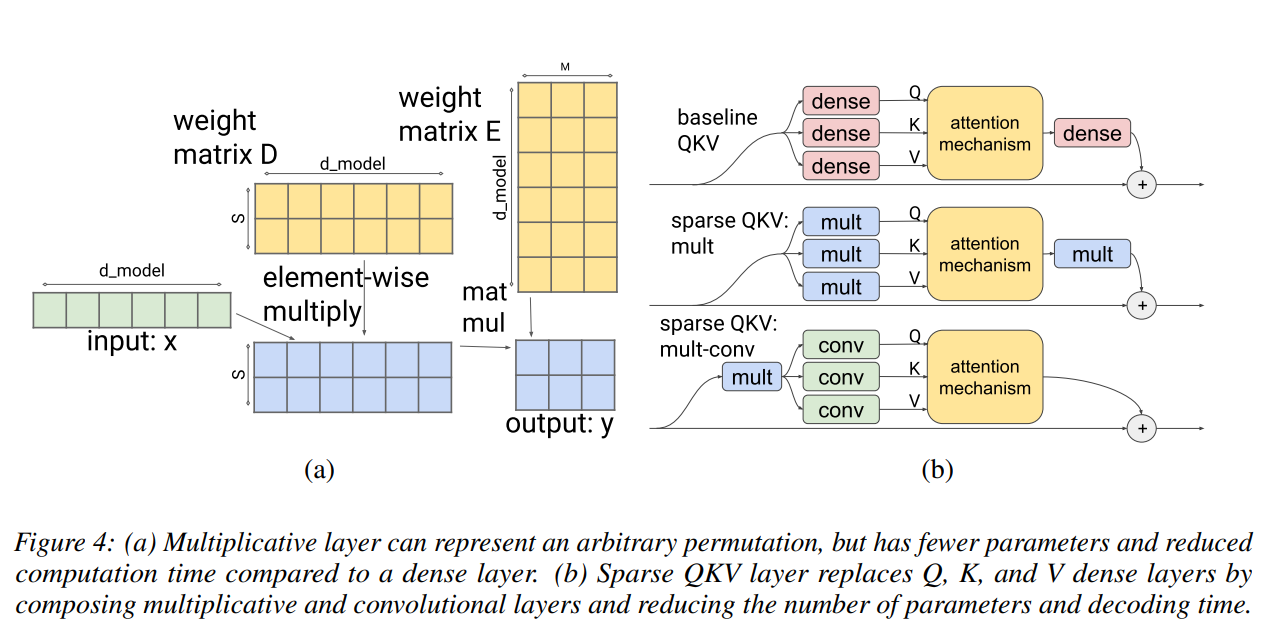
乘法密集层。我们新的乘法密集层可以表示任意排列，并且具有 d 2 /S + dmodel S 参数，具体取决于稀疏超参数 S。它通过将输入向量 x ∈ Rdmodel 分成大小为 M = dmodel/S 的 S 个“模块”来处理模型和输入向量。它产生输出 y ∈ RS×M 如下 sys,m = X xiDi,sEi,m i，其中两个权重矩阵是 D∈Rdmodel×S 和 E∈Rdmodel×M（见图 4（b））。由于参数数量减少，该层在推理过程中执行速度明显加快需要从内存中加载。除非另有说明，否则我们使用 S = 16。乘法层主要用于表示任何排列，以便每个注意力头都可以从嵌入的任何部分访问信息。我们首先验证乘法层确实可以表示任意排列（证明在附录中给出）。

定理 1. 对于任何双射函数 f：{1···dmodel} ⇒ {1···S} × {1 ···M}存在一对权重乘法层D，E使得xi = ys,m for {s, m} = f (i)。

卷积层。乘法层的输出是类型/形状 ∈ Rbatch×length×S×M 的张量。我们用二维卷积层处理这个张量，将模块 S 的长度维度和数量处理为图像的高度和宽度。该层使用 M 个过滤器和 F × F 的内核大小，以便每个过滤器查看最后 F 个标记（“长度”轴）的 F 个模块（“S”轴）。用这样的卷积代替标准的dense layer减少了参数QKV层的计数和计算时间。同时，通过在“长度”轴上进行卷积，模型可以将更多上下文纳入此计算 [23]。该层的输出与输入具有相同的形状。 S的最优值小于√dmodel。根据经验，我们将 F 设置为 3，S 等于注意力机制中的头数，M 为单个注意力头的维度。在这种情况下，我们可以将卷积的输出直接馈送到注意力机制，而无需重塑输出。该卷积层具有更少的参数 (9M2 + M = F2(dmodel/S)2 + (dmodel/S))，以及更低的计算复杂度 (O(d2 /S))。除非另有说明，否则我们使用 S = 16 和 F = 3。

modelCombining 乘法和卷积层。原始注意力机制中有四个密集层需要替换：Q、K、V 和输出。如图 4(b) 所示，我们通过组合乘法层和卷积层来替换 Q、K 和 V 密集层，但所有三个层共享一个乘法层：Q = convQ(mult(x)), K = convK(mult (x)), V = convV (mult(x))。我们移除输出密集层。请注意，组合乘法卷积变体移除了输出密集层，而其他变体将其替换为各自的稀疏层。包括这个输出层会对解码时间产生负面影响。我们可以将参数 S 设置为大约 √d 模型，与标准 QKV 层的 d 2 相比，层参数的数量与 d1.5 成比例缩放。

QKV层的模型解释。请注意，当卷积层中的参数 S 等于注意力机制中的头数时（在我们的实验中就是这种情况），那么每个 S 模块都对应一个注意力头。因此，该模型使用卷积来处理每个使用相同线性投影的头部。如果没有乘法层，该投影将在每个头的嵌入层的预定部分上运行。但是，通过添加它，模型可以执行任意维度排列，因此每个头都可以访问嵌入维度的任意子集，而不是预先确定的子集。尽管参数数量减少，但这一事实有助于保持生成的 QKV 层的可表达性。

消融。我们研究了稀疏 QKV 层对图 5 中相当于 T5-large 的模型的影响。我们将 dff 的值从 4096 增加到 6144 以保留参数数量（详见下一小节）。具有稀疏 QKV 层变体的解码时间与基线相似，因为它由密集的前馈层控制（详见附录）。

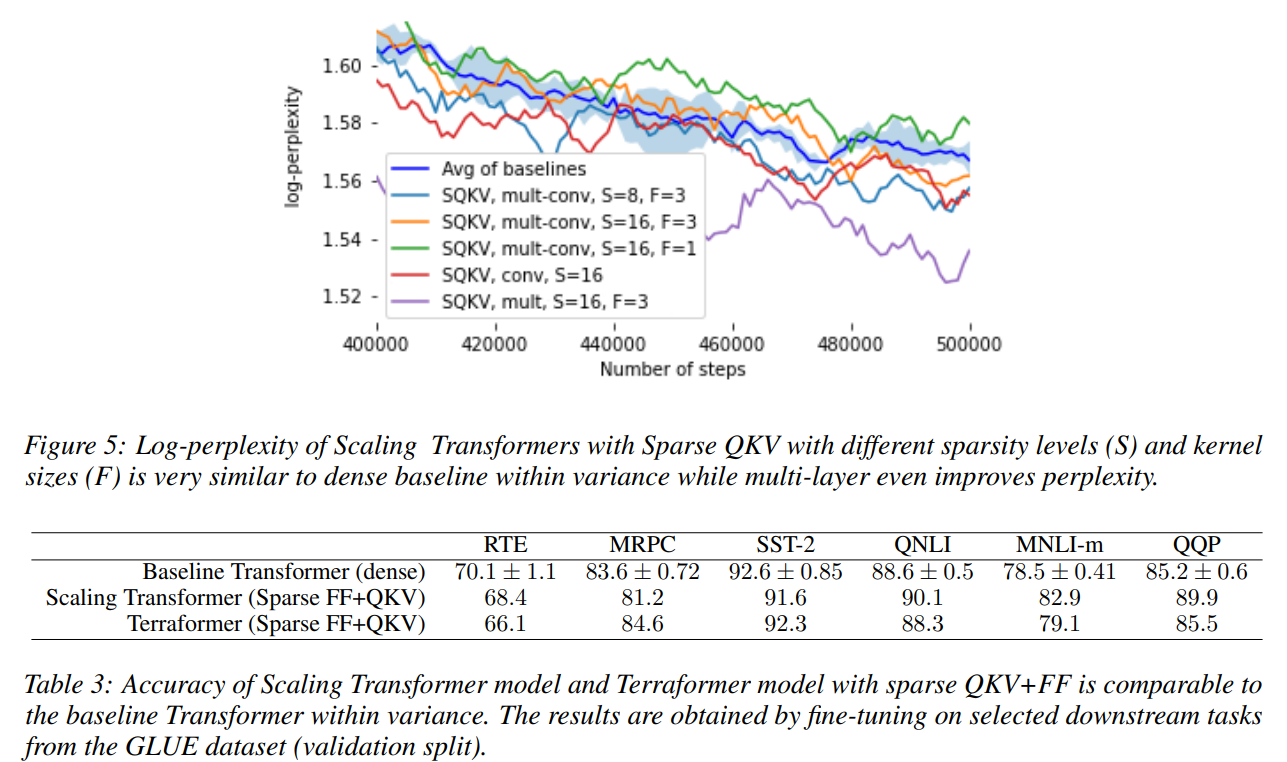
结合前馈和 QKV 稀疏性。稀疏的 QKV 层减少了模型参数的总数。为了使模型大小与基线匹配，我们增加了 dff 以保持我们比较的所有模型的参数数量相似。对于 T5-Large 等效模型，我们将 dff 从 4096 增加到 6144。随着 dff 的增加，前馈层中的解码时间增加，因此，单独的稀疏 QKV 层不会加速模型。然而，当我们将稀疏 QKV 层与稀疏 FF 层组合时，我们在每个解码块的解码时间上获得了 3.05 倍的加速类似的困惑（见表1和图1）。虽然基线是普通变形金刚，但重整机模型的解码速度也几乎相同。表3显示了从GLUE数据集微调下游任务模型的准确性。请注意，具有稀疏FF+QKV的模型达到的精度与基线相似.

3.3 稀疏损失层。

最后一个密集层将嵌入的模型映射到词汇表大小以计算损失。我们可以通过将密集层替换为类似于前面部分的乘法层来稀疏模型的这一部分;这加快了解码时间，但可能会降低混淆度。结果见附录。

4 长序列的稀疏性

上述稀疏化密集层的收益令人鼓舞，但我们忽略了一个基本问题。当应用于更长的序列时，增益实际上会丢失，因为解码时间将由注意操作决定。幸运的是，已经提出了许多方法来解决变形金刚的这个问题，参见 [41] 的调查。我们专注于 Reformer [19] 的 LSH（局部敏感散列）注意力，并展示如何将这种稀疏注意力机制以及循环块集成到缩放变换器中，从而产生 Terraformer.

4.1 长序列架构

同时集成稀疏注意力将层转换为 Scaling Transformer，我们注意到 Transformer 解码器块的架构不是最优的，可以重新设计以更好地利用这些层。特别是，从效率的角度来看，不再需要将解码器自注意力和编码器-解码器注意力分开。因此，我们移除了编码器-解码器注意力，但只是在解码器标记之前连接编码器表示。但是单独这样做是不够的，因为我们取消了一种注意力机制（编码器-解码器注意力）。我们通过在前馈块之前设置两个注意力机制来解决这个问题。这种简单的架构与基线 Transformer 一样快，同时提供更好的结果。

将它们放在一起，如果 venc 是编码器激活，vdec 是解码器嵌入，则解码器块 x 的输入是它们在长度轴上的串联，LengthConcat(venc ,vdec).
每个解码器块可以表示为：y1 = x + Dropout(Attention(LayerNorm(x))) y2 = y1 + Dropout(Attention(LayerNorm(y1)))y = y2 + FFN(y2)
其中 y 成为输入下一个解码器层。有关生成的体系结构的完整图表，请参见附录。

4.2 内存效率的可逆性

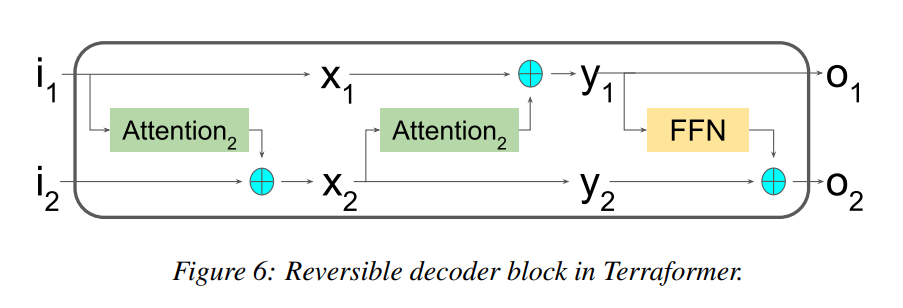
为了启用大批量训练 Terraformer，并在单台机器上微调大型模型，我们应用 Reformer [19] 的想法，特别是可逆层用于编码器和解码器块。原始 Reformer 解码器块包含 1-1 比例的前馈和注意层。在 Terraformer 架构中，如上所述，解码器块中有两个注意力层，因此解码器块中的可逆层中有三个交换（见图 6）。在我们的实验中，这显着提高了性能。可逆性的另一个问题是它仅在形式上对连续函数正确。我们发现这不仅仅是一个形式问题，而是实践中的一个重要问题。为了使可逆层能够很好地训练稀疏性，我们需要存储离散决策——即表示要选择哪些行的整数——并将它们用于逆向。在向后传递中重新计算这些决策会导致更糟糕的结果。

4.3 泛化的循环

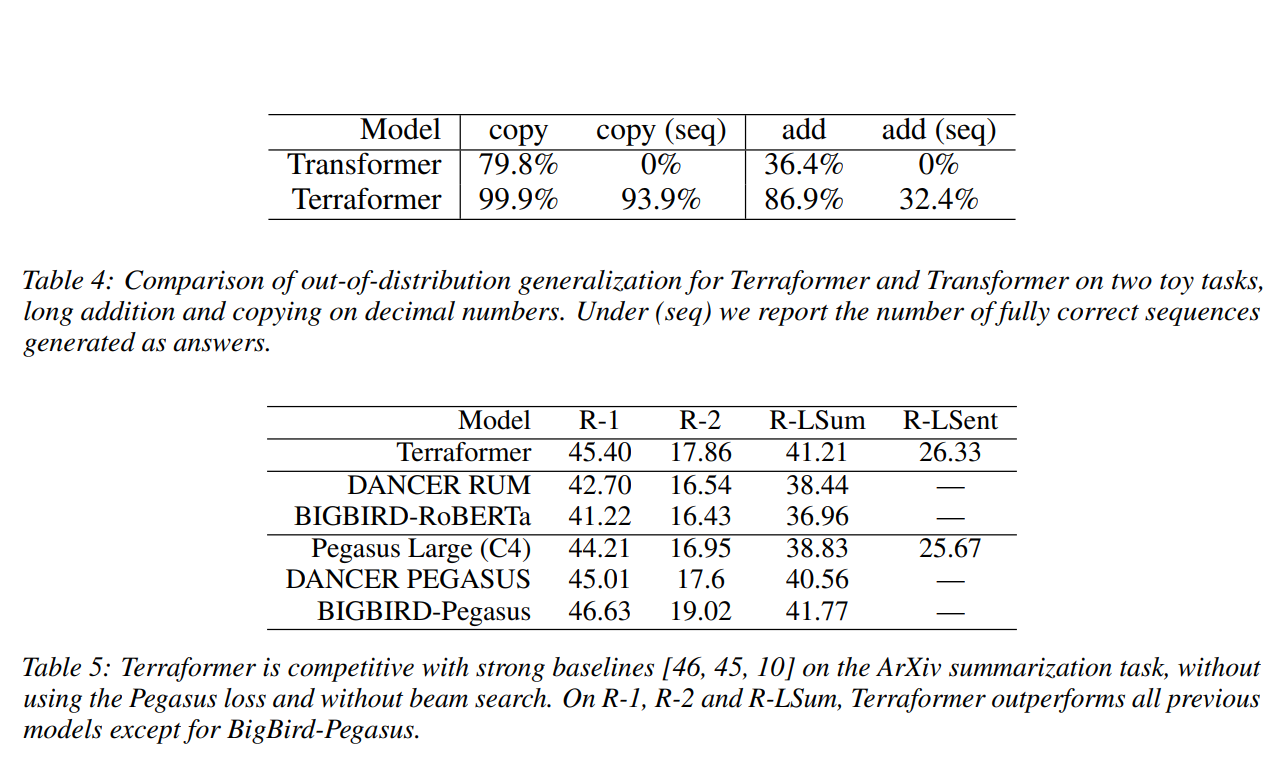
除了结合稀疏注意力和可逆性之外，我们还在 Terraformer 的前馈块中添加了循环。循环层允许信息及时传播，即使在单个解码器块中也是如此。尽管在不降低模型速度的情况下使用它们是具有挑战性的，尤其是。在培训中。出于这个原因，我们使用简单的循环单元 [20]，它们在训练期间可以很好地并行化。SRU 包含密集层，因此它们的使用可能会抵消其他地方稀疏性的好处。我们尝试了几种方法来缓解这种情况，但事实证明，简单地降低 SRU 的维度是有效的。所以我们首先从 dmodel 投影到一个小维度（在我们的实验中是 32），然后应用 SRU，然后投影回 dmodel 并将结果添加到前馈块中。这种低秩循环在我们的实验中足以通过时间传递足够的信息以供网络泛化。由于 SRU 对 C4 的影响很小（因为训练和评估数据非常相似），我们使用合成任务来调查-分布泛化。我们在长加法和复制十进制数字的任务上训练模型。我们训练最多 128 位数字的输入，并评估 256 到 300 之间的输入长度，因此长度超过 2 倍。如下表所示，基线 Transformer 的泛化效果不佳，而 Terraformer 设法正确地获得了很大一部分，即使它不像 Neural GPU [16] 那样完美。

4.4 实验

我们设计 Terraformer 的好处是稀疏性不会在长序列或下游微调任务中丢失。为了测试这一点，我们选择了总结科学论文的任务使用来自 arXiv3[6] 的科学论文数据集。在此任务中，输入是整篇论文——一个长序列——并要求模型输出其摘要。最近的几篇论文研究了这个数据集和任务，并且已经表明 [46, 45] 对 C4 的预训练在这个任务上产生了显着的改进。我们还在 C4 上预训练 Terraformer（就像本文中的所有实验一样），并在 arXiv 摘要任务上对其进行微调。我们发现 Terraformer 与上述基线相比具有竞争力，即使我们屏蔽了单个单词（我们不使用 Pegasus 句子损失）并以贪婪的方式解码答案（无波束搜索）。请注意，ROUGE 分数是使用开源记分器 4 及其文档 5 中描述的指标计算得出的。我们还观察到所报告的 ROUGE-L 指标之间存在一定的混淆。正如开源评分器中指出的那样，有两个版本的 ROUGEL-Sentence-Level (R-LSent) 和 ROUGEL-Summary-Level (R-LSum)。为清楚起见，我们报告了这两个指标。此外，我们只报告任何 ROUGE 指标的 F1 度量。我们在附录中包含了一些生成的摘要示例。

我们以与本文中报告的所有其他基线相同的方式对 Terraformer 进行了预训练，具有相同数量的参数 (800M)、与之前提到的相同维度和损失稀疏度 4 到获得最快的模型。与上一节中实现0.061s解码速度的稀疏Transformer模型相比，Terraformer实现了0.086s的解码速度，在perplexity方面的表现也差不多（详见附录）。我们还观察到，对于 GLUE 数据集上选定的下游任务，Terraformer 模型实现了类似于表 3 中的 Transformer 模型的精度。

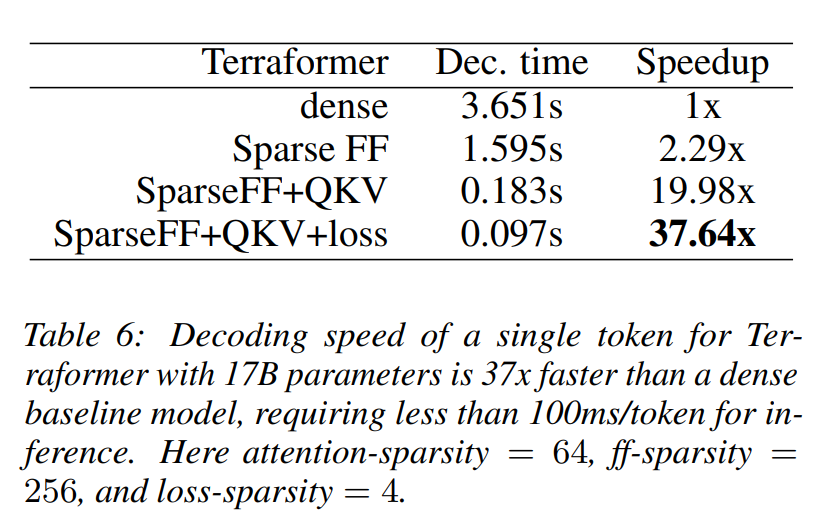
表 6 显示了当我们将 Terraformer 扩展到 17B 参数时使用稀疏层解码的加速。请注意，稀疏化所有层使我们的解码速度提高了 37 倍。

5 结论

当开始研究 Transformer 的稀疏变体时，我们假设会为稀疏性付出代价——稀疏模型的性能总是不如具有相同数量的密集模型的参数。令我们惊讶的是，情况并非如此：稀疏就足够了！
在我们对 C4 数据集上的大型模型进行的实验中，稀疏模型与密集模型的性能相匹配，同时推理速度要快很多倍。而且，当按比例放大模型时，稀疏性的好处变得更大。这有望让变形金刚回到可持续发展的轨道上，并使大型模型更有用。
当前的结果有许多局限性。首先，我们看到的实际加速仅用于推理，而不是在训练时。此外，我们考虑 CPU 上的非批处理推理，而推理通常在 GPU 上以批处理模式运行。我们相信，随着工作的增加，稀疏性也可以改善这些设置，因为我们的基本结果表明，稀疏模型与具有相同参数数量的密集对应模型达到相同的困惑度。
因此，当我们演示transformer是可能的，我们认为本文是迈向可持续大型模型的第一步。有许多技术可以使模型更快，这些技术可以极大地有益于 Terraformer 和其他 Scaling Transformer。例如，我们没有研究量化，我们相信它可以使 Scaling Transformers 更快。我们还专注于推理速度，但训练速度没有得到提高。主要原因是我们在训练前馈块时使用了 Gumbel-Softmax（参见第 3.1 节）。费杜斯等人。 [8] 已经提供了一个有前途的替代方案，我们期待在未来的工作中对其进行探索。此外，我们希望社区能从 Scaling Transformers 中获得灵感，并根据他们的需要调整它们。我们使用从密集 Transformer 借来的层大小和超参数进行实验，它们很可能不是 Scaling Transformer 的最佳选择。通过适当的调整和进一步的改进，我们相信人们可以训练一个 Scaling Transformer 在准确性上与 GPT-3 相匹配，但也可以在笔记本电脑上以合理的时间运行推理。我们将其视为对社区的一项迷人挑战，因为这种 Scaling Transformers 不仅更具可持续性，而且还将使每个人都可以使用大型模型。

这篇关于【论文阅读】Sparse is Enough in Scaling Transformers的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---