本文主要是介绍uva10020Minimal Coverage,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
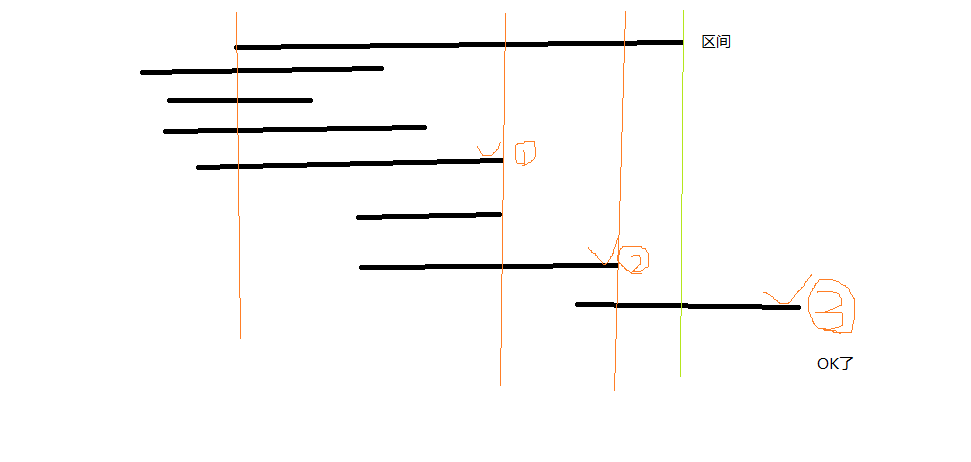
题意:数轴上,用给出的线段去覆盖[0,M]段,M也是输入的,要求所用的线段数量最小。
解题:贪心算法。秘诀:先将所有跟[0,M]无关的线段扔掉(线段的右端点<0 或者 线段的左端点>M),在将所有的线段以左端点排序,先第一步找左端点<=0的线段中右端点最长的,记录下右端点end,然后将[0,M]变成[end,M],在以end为左端点找下一条线段(即找左端点<=end的线段中右端点最长的),直到找到的右端点>=M;此题还要求打印用到的线段,那么就将用的线段用visited标记下好了。
代码:
/*
uva 10020 Minimal Coverage
AC By Warteac
2013-4-13
Runtime:0.200s
*/
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
/
struct node{ //segment
int s; //strat position
int e; //end position
node(int x,int y){s = x; e = y;}
};
class MinimalCoverage{
private:
int cal(int e);//返回左端点比e小且右端点最大的线段的右端点,并且在visited 中标记此条线段
int M;
vector <node> segment;
vector <int> visited;
int sum;
public:
void initial();
void readCase();
void computing();
void outResult();
};
int MinimalCoverage::cal(int e){
int max = e,i,j = 0;
for(i = 0; (segment[i].s <= e)&& (i < segment.size()); i++){ //左端点小于e
if(segment[i].e > max){ //右端点最大
max = segment[i].e;
j = i; //记下线段的序号
}
}
if(max) visited.push_back(j); //在visited中记录下找到的线段
return max;
}
bool cmp(node n1,node n2){
return (n1.s < n2.s);
}
void MinimalCoverage::initial(){
segment.clear();
M = 0; sum = 0;
visited.clear();
}
void MinimalCoverage::readCase(){
int a,b;
cin >> M;
while((cin >> a >> b) && (a || b)){
if( a > M || b < 0) //第一步筛除与[0,M]无关的线段;
continue;
else
segment.push_back(node(a,b));
}
}
void MinimalCoverage::computing(){
int end = 0,temp = 0;
sort(segment.begin(),segment.end(),cmp);//根据左端点排序
if((segment[0].s > 0)){ //第一条的左端点大于0,不可能覆盖
sum = 0;
}
else {
while(end < M){//右端点没有覆盖到M
end = cal(end); //去找下一条线段覆盖后的右端点
//cout << "end = "<<end<<endl;
temp++; //线段计数
if(end ==0) break; //如果其中断掉了,cal返回0
}
if(end >= M) sum = temp; //覆盖成功
}
}
void MinimalCoverage::outResult(){
cout << sum <<endl;
if(sum)
for(int x = 0; x < visited.size(); x++){
cout << segment[visited[x]].s <<" "<< segment[visited[x]].e <<endl; //输出被标记的线段
}
cout<<endl;
}
/
int main(){
MinimalCoverage mc;
int n;
cin >> n;
while(n--){
mc.initial();
mc.readCase();
mc.computing();
mc.outResult();
}
return 0;
}
这篇关于uva10020Minimal Coverage的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!