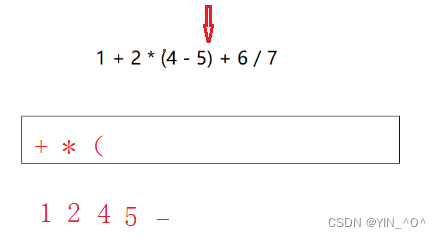栈的表达式求值中的应用——逆波兰表达式求值+中缀表达式转后缀表达式

本文主要是介绍栈的表达式求值中的应用——逆波兰表达式求值+中缀表达式转后缀表达式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 逆波兰表达式（后缀表达式）求值

链接: link

这道题目叫做逆波兰表达式求值，那什么是逆波兰表达式呢？
我们可以一起来了解一下：

结合题目中给的测试用例给大家解释一下：

我们正常写的表达式，就比如题目中的这个：(2 + 1) * 3
这种写法叫做中缀算术表达式，即运算符写在操作数的中间，但是这种写法计算机是不能直接计算的，因为涉及运算符优先级的问题，比如1+2*3，应该先算*。
所以呢，这里就需要我们做一件事情，就是把它变成后缀表达式，其实就是根据优先级对表达式中的运算符排一个序，并且放到对应的操作数后面。
就比如题目中给的这个示例：((2 + 1) * 3)这个表达式对应的后缀表达式就是["2","1","+","3","*"]（题中是把它放到一个字符串数组中了）。
即1和2先进行后面的+，得到的结果再和3进行后面的*，得到最终结果。这样就直接从前往后算，不用考虑优先级的问题了。

那现在大家对逆波兰表达式应该有一个大致的了解了。

思路讲解

但是呢，单要解这道题目的话，其实很好搞：

我们只需要借助一个栈就搞定了。
具体怎么做呢？
我们去遍历给的逆波兰表达式对应的字符串数组，如果对应的元素是数字，我们就让该操作数入栈，如果遇到操作符，我们就去取栈顶的前两个元素（并pop掉）进行对应的运算（第一个是右操作数，第二个是左操作数），然后将结果入栈，后续重复上述操作，最终栈里面唯一的那个元素就是要求的结果。
举个栗子：

遍历tokens，2 1入栈，接着遇到+，取出 1 2相加，得到结果3入栈，后面又是一个3入栈，接着遇到* ，取出3 3相乘，结果9入栈。
最终栈里面唯一的元素9就是结果。

AC代码

class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> st;for(auto& str:tokens){if(str=="+"||str=="-"||str=="*"||str=="/"){int right=st.top();st.pop();int left=st.top();st.pop();switch(str[0]){case '+':st.push(left+right);break;case '-':st.push(left-right);break;case '*':st.push(left*right);break;case '/':st.push(left/right);break;}}else{st.push(stoi(str));}}return st.top();}
};

2. 中缀表达式转后缀表达式

那现在大家再来思考一个问题：
如果给我们一个中缀表达式，我们如何把它转换成对应的后缀表达式？

分析

那中缀转后缀呢，也是需要借助一个栈，具体怎么做呢？
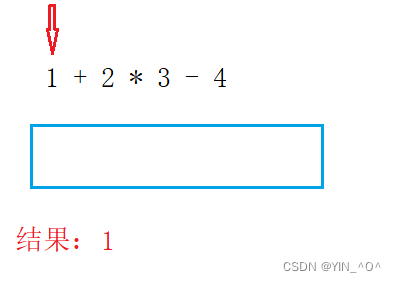
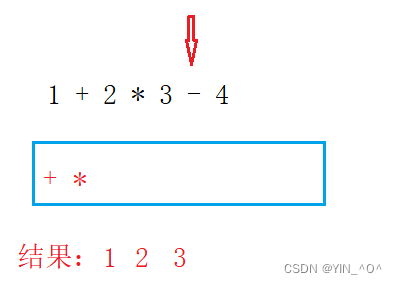
比如现在有这样一个中缀表达式1+2*3-4
怎么把它转成后缀呢？
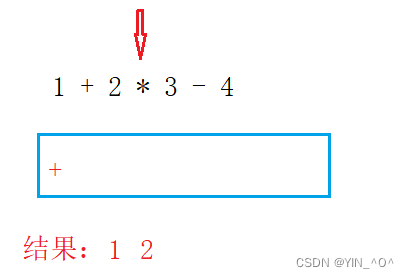
🆗，我们还是从头去遍历这个表达式，如果遇到的是操作数，就输出；

如果遇到的是的是操作符，那这时要分情况进行分析：
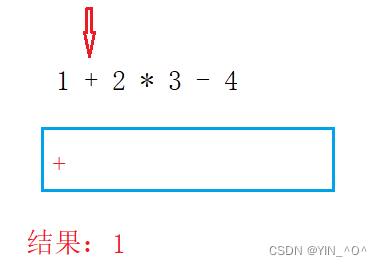
如果此时栈为空，就让该操作符进栈；


如果遇到的是操作符，且此时栈不为空，则取栈顶的操作符与当前操作符比较，比较啥呢——优先级：
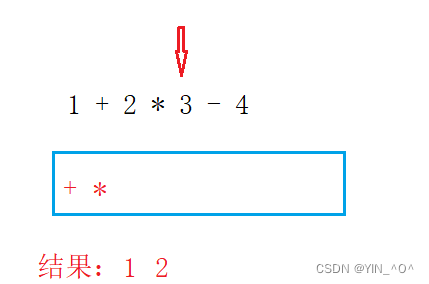
如果比栈顶操作符优先级高，就让该操作符进栈，为什么是进栈而不是拿它进行运算呢？
因为后面有可能还有优先级更高的，所以先进栈。

那进栈之后呢？继续取下一个进行判断是操作数还是操作符。

如果比栈顶操作符优先级低或者相等，则出栈顶的操作符输出（即此时栈顶的这个操作符可以进行运算了）

然后再去判断栈是否为空，不为空再拿当前操作符和栈顶操作符比较，进行相应操作，为空就入栈。



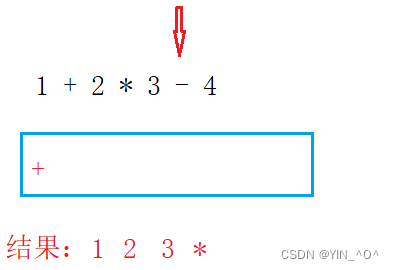
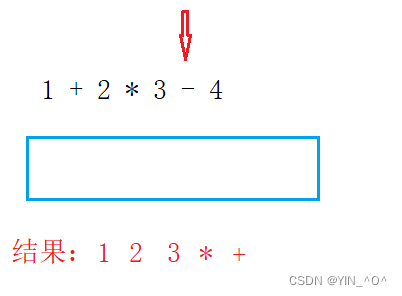
遍历结束后，如果栈不为空，将剩余操作符输出。

此时，就得到对应的后缀表达式了。

但是，如果是带括号的情况呢？

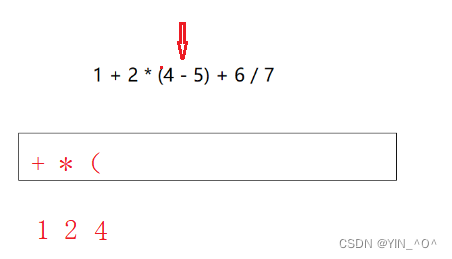
比如1+2*(4-5)+6/7，怎么处理？
🆗，那如果按照上面的分析，1输出，+入栈，2输出，*的优先级比栈顶的+高，*也入栈，接着遇到了括号，怎么办？

如果不加括号的话，后面-比*优先级低，那应该让*先出栈运算，但是现在-在括号里面，所以-应该先运算，所以要认为-的优先级更高。
那我们可以怎么处理呢？当然这里的方法可能不止一种，我们可以这样做：
遇到(，我们认为它的优先级很低，但是我们不拿(做比较，直接让它入栈

然后遇到括号里的-，栈不为空，比较，因为我们说了认为(的优先级很低，所以-也入栈

那继续往后走遇到)怎么办？
🆗，)呢我们也认为它的优先级很低，但是)我们要拿它去比较，因为我们认为)优先级很低，所以此时栈顶的-是不是就被成功弹出了。

然后栈不为空继续跟栈顶比，那此时) 就遇到 (了，拿这时怎么做呢？
这时直接把(pop掉，不输出，然后跳过) 继续看下一个，因为后缀表达式优先级都排好了就不需要括号了。

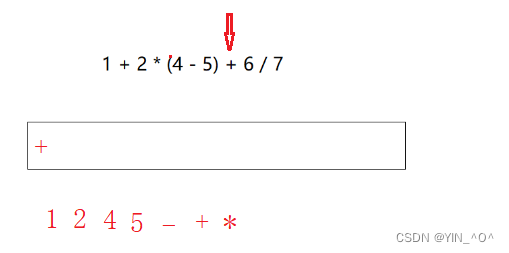
拿继续往后走遇到+，栈不为空，跟栈顶比，比栈顶优先级低，栈顶操作符*输出，继续栈还不为空，继续比，优先级相等，出栈顶操作符+

然后栈空了，+入栈

然后遇到6输出，遇到/优先级比+高，入栈，然后7输出

就遍历完了，再把剩余操作符输出

就得出结果后缀表达式了，大家可以验证一下。

当然处理括号可能有很多种方法，我们这里提供的只是其中一种，而且我们这种方法如果遇到有些极端的情况可能也不一定处理的了，可能还需要加一些特殊处理。
另外我们会发现就是遇到(是不是好像去开了一个新栈，在这个新栈里去处理括号里的这个子表达式，所以如果这样的问题也可以考虑递归去搞，每次遇到(就递归去处理这个子表达式，处理完回去递归调用的地方继续处理后面的。

方法总结

3. 中缀表达式求值

那大家再来思考一下，如果给一个中缀表达式，我们该如何求它的值呢？

🆗，是不是就是上面两种操作的结合啊。

这篇关于栈的表达式求值中的应用——逆波兰表达式求值+中缀表达式转后缀表达式的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---