常见排序算法巩固附上经典视频教程

冒泡排序

public static int[] bubbleSort(int[] array) {for (int i = 0; i < array.length; i++) {for (int j = 0; j < array.length-i-1; j++) {if (array[j] > array[j+1]) {int temp = array[j];array[j] = array[j+1];array[j+1] = temp;}}}return array;}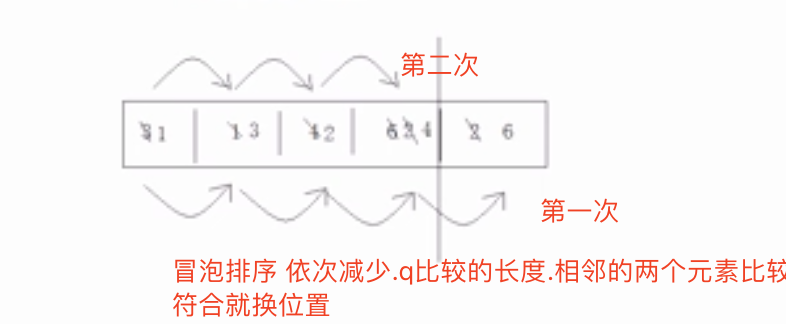

image.png

上面的代码是把每一个进行遍历然后写一个内循环进行啰嗦重复的遍历
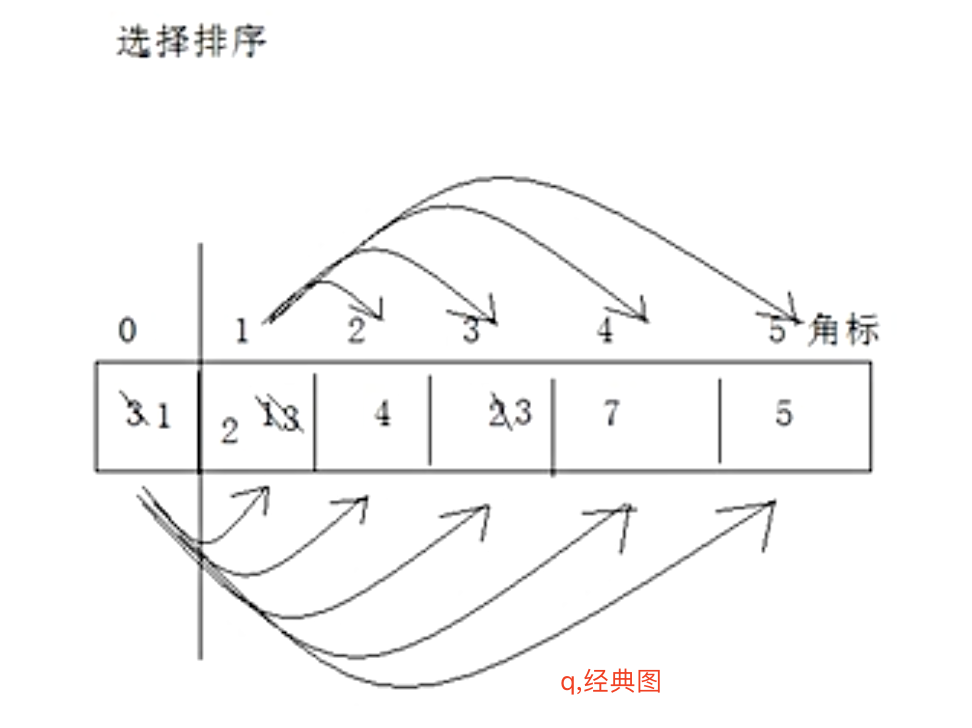
选择排序

public static int[] selectSort(int[] array) {for (int i = 0; i < array.length - 1; i++) {//最后一个不需要比较了,for (int j = i+1; j < array.length; j++) {if (array[i] > array[j]) {int temp = array[i];array[i] = array[j];array[j] = temp;}}}return array;}

选择排序的特点是一次从头开始往后面比较,每次循环 头部开始位置就会+1,
冒泡排序不同,冒泡排序是相邻的2个进行比较, 如0和1 的索引值比较完毕之后 1 和 2 比较 ,
插入排序

public static int[] sort(int[] array) {for (int i = 1; i < array.length; i++) {int temp = array[i];int in = i;while (in > 0 && array[in-1] >= temp) {array[in] = array[in-1];in--;}array[in] = temp;}return array;}

快速排序
看官方的脑壳不够用

/*** Sorts the specified range of the array using the given* workspace array slice if possible for merging** @param a the array to be sorted* @param left the index of the first element, inclusive, to be sorted* @param right the index of the last element, inclusive, to be sorted* @param work a workspace array (slice)* @param workBase origin of usable space in work array* @param workLen usable size of work array*/static void sort(long[] a, int left, int right,long[] work, int workBase, int workLen) {// Use Quicksort on small arraysif (right - left < QUICKSORT_THRESHOLD) {sort(a, left, right, true);return;}/** Index run[i] is the start of i-th run* (ascending or descending sequence).*/int[] run = new int[MAX_RUN_COUNT + 1];int count = 0; run[0] = left;// Check if the array is nearly sortedfor (int k = left; k < right; run[count] = k) {if (a[k] < a[k + 1]) { // ascendingwhile (++k <= right && a[k - 1] <= a[k]);} else if (a[k] > a[k + 1]) { // descendingwhile (++k <= right && a[k - 1] >= a[k]);for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) {long t = a[lo]; a[lo] = a[hi]; a[hi] = t;}} else { // equalfor (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) {if (--m == 0) {sort(a, left, right, true);return;}}}/** The array is not highly structured,* use Quicksort instead of merge sort.*/if (++count == MAX_RUN_COUNT) {sort(a, left, right, true);return;}}// Check special cases// Implementation note: variable "right" is increased by 1.if (run[count] == right++) { // The last run contains one elementrun[++count] = right;} else if (count == 1) { // The array is already sortedreturn;}// Determine alternation base for mergebyte odd = 0;for (int n = 1; (n <<= 1) < count; odd ^= 1);// Use or create temporary array b for merginglong[] b;                 // temp array; alternates with aint ao, bo;              // array offsets from 'left'int blen = right - left; // space needed for bif (work == null || workLen < blen || workBase + blen > work.length) {work = new long[blen];workBase = 0;}if (odd == 0) {System.arraycopy(a, left, work, workBase, blen);b = a;bo = 0;a = work;ao = workBase - left;} else {b = work;ao = 0;bo = workBase - left;}// Mergingfor (int last; count > 1; count = last) {for (int k = (last = 0) + 2; k <= count; k += 2) {int hi = run[k], mi = run[k - 1];for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) {if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) {b[i + bo] = a[p++ + ao];} else {b[i + bo] = a[q++ + ao];}}run[++last] = hi;}if ((count & 1) != 0) {for (int i = right, lo = run[count - 1]; --i >= lo;b[i + bo] = a[i + ao]);run[++last] = right;}long[] t = a; a = b; b = t;int o = ao; ao = bo; bo = o;}}

image.png

不过原理就是把数据分成两部分进行排序,有一个图非常清晰的,

从上面插入排序代码看上去好像差不多的样子,但是while循环的条件是和当前index-1以及-....都要比外循环index的值才进行不断的内while循环递减替换比较,不满足就不会进行了,所以优点就是处理有序数量较多的时候有优势.

image.png