大白话KMP算法

本文主要是介绍大白话KMP算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

KMP算法

最近刷左神的体系学习班，正好学习到了KMP算法，这里对其做一个整理，以最直白的方式介绍KMP算法。

KMP算法简介

在计算机科学中，Knuth–Morris–Pratt algorithm字符串查找算法（简称为KMP算法），可在一个字符串str1 内查找一个词str2 的出现位置，作用类似于 Java 中 str1.indexOf(str2)。

前缀函数

KMP算法的核心之一就是引入了前缀函数的概念，该函数也是解决子串问题的核心函数。

前缀函数介绍

KMP算法的核心之一就是引入了前缀函数的概念，那么什么是前缀函数呢？

为了便于计算，我们将 Leetcode 中关于前缀函数的计算规则稍作改变：

对于长度为 m 的字符串 s，其前缀函数 π(i+1)(0≤i<m) 表示 s 的子串 s[0:i] 的最长的相等的真前缀与真后缀的长度。
特别地，如果不存在符合条件的前后缀，那么 π(i)=0。其中真前缀与真后缀的定义为不等于自身的的前缀与后缀。

说人话，就是字符串任一位置的前缀函数，表示该位置之前的字符的真前缀与真后缀字符都能完全匹配的最大长度。

这里的真前缀就是说不能表示该位置之前所有的字符串，真后缀也是类似。举个例子，假设一个字符串来到了索引位置（从0开始）为6的位置，前面五位为 hello，那么真前缀为 h,he,hel,hell，hello不是真前缀，因为它包含了前面整个字符串。同理，真后缀为 o,lo,llo,ello。

有了这个概念，我们可以来看一个前缀函数的例子：求字符串 aabaaab 的前缀函数

π(0)=-1，人为规定，方便后面计算
π(1)=0，因为 a 没有真前缀和真后缀，根据规定为 0（对于任意字符串 π(1)=0 必定成立）
π(2)=1，因为 aa 最长的一对相等的真前后缀为 a，长度为 1；
π(3)=0，因为 aab 中没有完全相等的真前缀与真后缀，因此值为0；
π(4)=1，因为 aaba 最长的一对相等的真前后缀为 a，长度为 1；
π(5)=2，因为 aabaa 最长的一对相等的真前后缀为 aa，长度为 2；
π(6)=2，因为 aabaaa 最长的一对相等的真前后缀为 aa，长度为 2；

前缀函数求解

详细证明过程可以参考 Leetcode，这里主要直观介绍如何求解，并对主要过程简单证明

由前述内容，我们知道了对于任何长度大于1的字符串，必然有 π(0)=-1，π(1)=0，我们从 π(2) 开始逐项求解。

由于是从左往右逐项求解，那么我们在求解 π(i+1) 时，必然已经知道 π(i) 的值了，假设 π(i) = x，那么必然有 π(i+1) <= x+1

简单证明一下：

由于 π(i) = x，如果索引为 x 的位置的字符与 i 位置的字符相等，那么真前后缀相等的长度可以达到 x+1。

现在要证明该长度不能大于 x+1

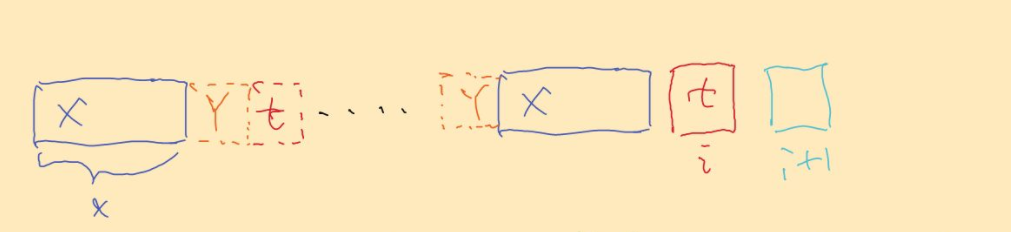
我们假设该长度可以大于 x+1，那么必定存在如下图所示的 Y 区域，使得 X+Y+t = Y+X+t，我们可以看到 X+Y 这一段区域与 Y+X 这一段区域是相等的，而且长度 > x，且都在 i 范围内，那么有 π(i) > x，这与前面的假设是相悖的，所以必然有 π(i+1) <= x+1

知道这一点，我们接着看看如何求解。

假设我们知道 π(i) = x ，我们定义一个 cn 指向 x 索引位置的字符。此时，比较字符串 x 的位置与 i 位置的字符是否相等

如果相等，由于前面已经证明 π(i+1) <= x+1，那么已经找到了 π(i+1) ，值为 cn+1，此时继续求解 π(i+2) 的值即可。
- 如果不等，那么我们将 cn 指向 x1 = π(x) 的索引上，比较 x1 位置与 i 位置字符是否相等
  - 如果相等，说明找到结果了，继续求解 π(i+2) 的值即可。
  - 如果不等，继续查找 cn 指向 x2 = π(x1) 的索引位置上，比较 x2 位置与 i 位置字符是否相等

循环上面的过程直到找到结果，如果cn都走到0位置了，仍然没有匹配，那么有 π(i+1) = 0。

案例如下：

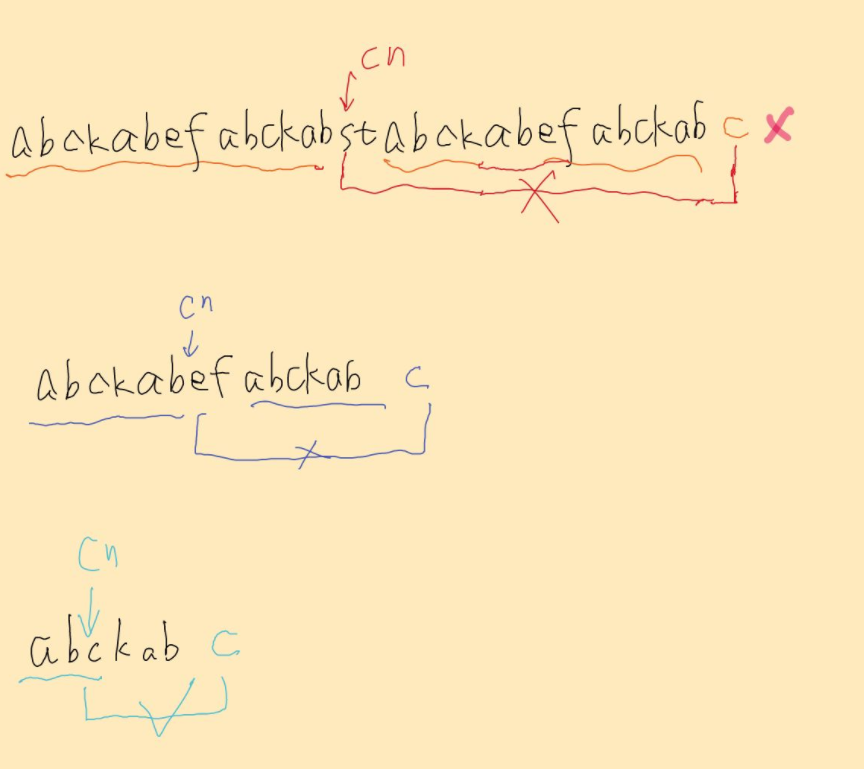
下面我们简单讲一下为什么可以这么操作：

正着看不太直观，我们反向看这个过程。

假设迭代到第 n 次时，字符刚好为i 位置字符 t，假设前缀为 A，那么子串An的末尾也必然为A。

看看第n-1次，由于A(n-1)中必然以子串An结尾，因此A(n-1)也必然以A结尾。

以此类推，必然有A1以A结尾，于是可以得到在 i+1位置上的一个满足条件的前缀。

Java实现

        private static int[] getNextArray(char[] str2) {if (str2.length == 1) {return new int[]{-1};}int n = str2.length;int[] next = new int[n];next[0] = -1;next[1] = 0;// 当前来到 i 位置开始寻找int i = 2;// cn表示 char next，用来寻找与 i 位置前一个字符相匹配的子串的位置int cn = 0;while (i < n) {if (str2[i - 1] == str2[cn]) {next[i++] = ++cn;} else if (cn > 0) {cn = next[cn];} else {next[i++] = 0;}}return next;}

其它的应该没有啥疑问，主要讲解一下 16 行 next[i++] = ++cn;这一句的理解。

由前面的求解过程我们可以知道，走到这个分支以后，实际上已经找到 next[i] 的值为 cn+1。

然后我们需要找 next[i+1] 的值，因此需要 i++。

同时，我们知道next[i] = cn + 1，那么对于 next[i+1] 需要从索引为 next[i] 的位置开始匹配，因此需要对 cn++。

也就是需要执行如下过程

    next[i] = cn + 1;i++;cn++;

上面三行代码干的事情可以用一行来简化，也就是

    next[i++] = ++cn;

时间复杂度

由于 cn 有增加也有减小不太好观察，那么我们观察 i 以及 i - cn 的变化情况

分支	i变化	i-cn变化
str2[i - 1] == str2[cn]	↑	→
cn > 0	→	↑
next[i++] = 0	↑	↑

由于 i 的变化范围是 0~m，i-cn变化范围也是 0~m

对于不同分支 i 和 i-cn都是单调增加的，而且至少有一个是必须增长（没有同时不变的情况），由于循环中至少进入一个分支内，因此最长情况下经历的步骤为 m + m，因此时间复杂度为 O(m)。

文本匹配

求解过程

求解问题： s1 中 s2 字符串出现的位置

首先，必然有s1 的长度 >= s2 的长度，否则，一定找不到子串与 str2 相等，这种情况直接过滤掉。

好了，现在介绍一下如何操作，假设S1在i 到 X-1 之间与S2 在 0 到 Y - 1之间都是完全匹配的，但是X位置与Y位置的字符不同。

记S2在此处的前缀函数为π(Y) ， j=X-π(Y) ，现在只需要将X的开头挪到 j 位置继续比较即可（注意：这里将X挪到j位置是一个逻辑上的概念，代码实现放到后面讲）。移动完成后，S1与S2的前面的π(Y)位一定是相等的，直接从后面一位开始比较即可。

根据上面的分析，这一个过程与固定住 X 然后将 S2的Y位置移动到π(Y)位置是等价的。

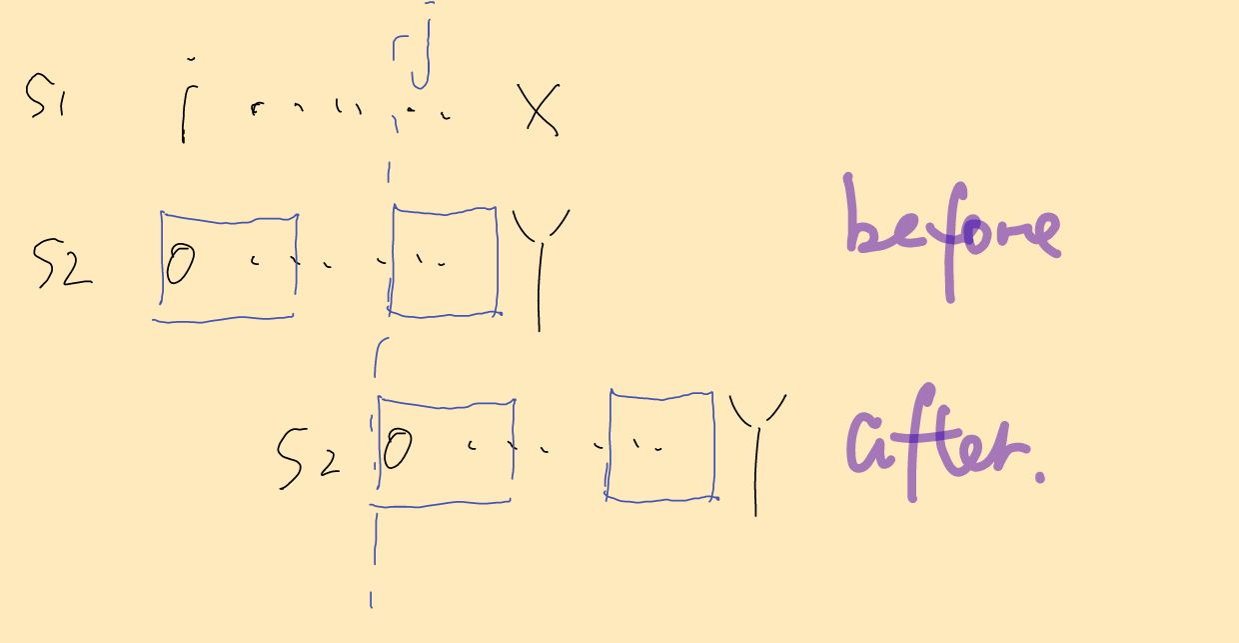
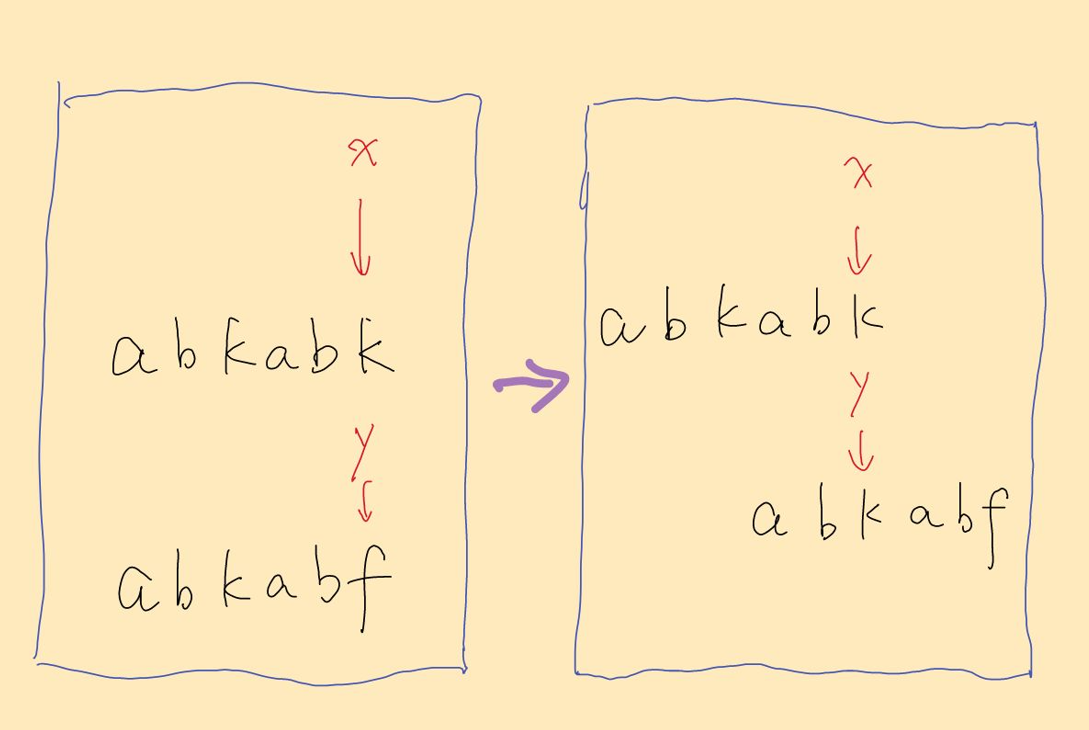
举个例子，如下图所示，S1在0~4与S2在0~4位置都相同，现在需要在第5个位置不同，现在需要将S2的π(5)=2 与X对齐

理解了上面过程，现在讲一下 为什么在 i到j 这段区间内不存在答案

如下图所示，假设 S1 从i到j这段中间的k位置开始的子串与S2是相等的

由于S1在i到X-1与S2在0~Y-1这一段完全相同，那么必然有k 与 kpost是相等的
由于k开头的字符串与S2全等，那么k开头的字符串与S2中开头的字符串也必然相等，也即是说 k 与kpre是相等的

由此可以推导出：kpre 与 kpost 相等，由于这两个分别是S2在Y索引上的真前缀以及真后缀，而且该长度大于 π(Y)，出现了矛盾，因此 在 i到j 这段区间内不存在答案

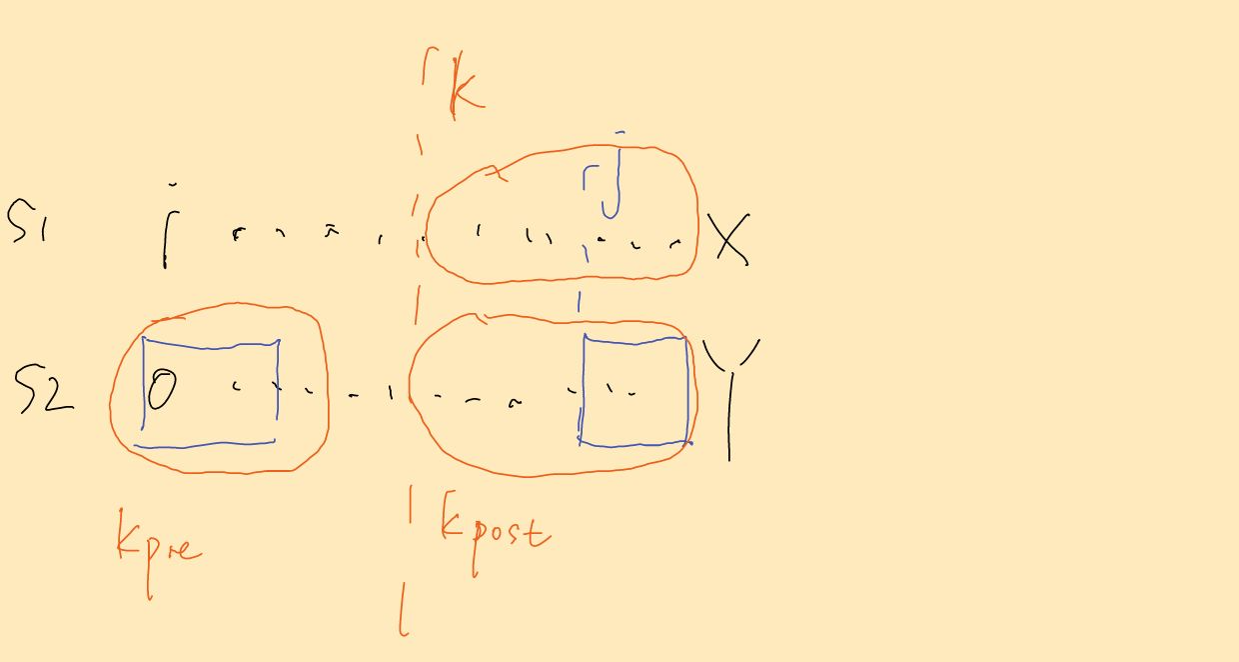
代码实现

        public static int getIndexOf(String s1, String s2) {if (s1 == null || s2 == null || s2.isEmpty() || s1.length() < s2.length()) {return -1;}char[] str1 = s1.toCharArray();char[] str2 = s2.toCharArray();int[] next = getNextArray(str2);// x 用来记录 str1 目前查看的位置, y 用来记录 str2 目前查看的位置int x = 0;int y = 0;while (x < str1.length && y < str2.length) { // str1 和 str2 都还没走完才需要继续比较if (str1[x] == str2[y]) {// 相等, 比较下一个位置x++;y++;} else if (y != 0) { // y != 0 或者说 next[y] != -1// y 还能冲一冲y = next[y];} else {// 确实找不到了//x++;}}// y 走到最后了说明已经找到了, 否则说明未找到return y == str2.length ? x - y : -1;}

文本匹配时间复杂度

先看一下 while 循环中的时间

由于 y 有时增加有时减少不太好观察，那么我们观察 x 以及 x - y 的变化情况

分支	x变化	x-y变化
x++;y++;	↑	↑
y = next[y];	→	↑
x++;	↑	→

由于 x 的变化范围是 0~n，x-y变化范围也是 0~n

对于不同分支 x 和 x-y都是单调增加的，而且至少有一个是必须增长（没有同时不变的情况），由于循环中至少进入一个分支内，因此最长情况下经历的步骤为 n + n，因此时间复杂度为 O(n)。

总体时间复杂度

上面只分析了迭代过程，现在对加上前缀函数求解的总体时间复杂度进行估算

当 m > n 时，直接返回-1了
当 m <= n 时，整体的时间复杂度应该是 O(m) + O(N) = O(N)

因此，整体的时间复杂度为 O(N)

整体代码与对数器

    public class KMP {public static void main(String[] args) {comp();}public static int getIndexOf(String s1, String s2) {if (s1 == null || s2 == null || s2.isEmpty() || s1.length() < s2.length()) {return -1;}char[] str1 = s1.toCharArray();char[] str2 = s2.toCharArray();int[] next = getNextArray(str2);int x = 0;int y = 0;while (x < str1.length && y < str2.length) {if (str1[x] == str2[y]) {// 相等, 比较下一个位置x++;y++;} else if (y != 0) { y = next[y];} else {x++;}}// y 走到最后了说明已经找到了, 否则说明未找到return y == str2.length ? x - y : -1;}private static int[] getNextArray(char[] str2) {if (str2.length == 1) {return new int[]{-1};}int n = str2.length;int[] next = new int[n];next[0] = -1;next[1] = 0;// 当前来到 i 位置开始寻找int i = 2;// cn表示 char next，用来寻找与 i 位置前一个字符相匹配的子串的位置int cn = 0;while (i < n) {if (str2[i - 1] == str2[cn]) {next[i++] = ++cn;} else if (cn > 0) {cn = next[cn];} else {next[i++] = 0;}}return next;}/*** for test*/public static String getRandomString(int possibilities, int size) {char[] ans = new char[(int) (Math.random() * size) + 1];for (int i = 0; i < ans.length; i++) {ans[i] = (char) ((int) (Math.random() * possibilities) + 'a');}return String.valueOf(ans);}private static void comp() {int possibilities = 25;int strSize = 30;int matchSize = 10;int testTimes = 5000000;System.out.println("start...");for (int i = 0; i < testTimes; i++) {String str = getRandomString(possibilities, strSize);String match = getRandomString(possibilities, matchSize);if (getIndexOf(str, match) != str.indexOf(match)) {throw new RuntimeException("Oops!");}}System.out.println("finish...");}}