【数据结构（邓俊辉）学习笔记】向量05——排序器

本文主要是介绍【数据结构（邓俊辉）学习笔记】向量05——排序器，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0. 概述

介绍下有序向量的排序器，包括起泡排序和归并排序。

1.统一入口

这类接口也是将无序向量转换为有序向量的基本方法和主要途径

2. 起泡排序

2.1 起泡排序（基础版）

2.1.1 算法分析

2.1.2 算法实现

反复调用单趟扫描交换算法，直至逆序现象完全消除。

template <typename T> //向量的起泡排序
void Vector<T>::bubbleSort ( Rank lo, Rank hi ) //assert: 0 <= lo < hi <= size
{ while ( !bubble( lo, hi-- ) ); } //逐趟做扫描交换，直至全序

算法思想：依次比较各对相邻元素，每当发现逆序即令二者彼此交换；一旦经过某趟扫描之后未发现任何逆序的相邻元素，即意味着排序任务已经完成，则通过返回标志“sorted”，以便主算法及时终止。

template <typename T>
void Vector<T>::bubble ( Rank lo, Rank hi) { //0 <= nbool sorted = true; //整体排序标志while ( ++lo < hi ) { //自左向右，逐一检查各队相邻元素if ( _elem[lo - 1] > _elem[lo] ) { //若逆序，则sorted = false; //因整体排序不能保证，需要清除排序标志swap ( _elem[lo - 1], _elem[lo]); //交换}}return sorted;
} //借助布尔型标志位sorted，可及时提前退出，而不致总是蛮力地做n - 1趟扫描交换

2.1.3 重复元素与稳定性

稳定算法的特征是，重复元素之间的相对次序在排序前后保持一致。

该起泡排序过程中元素相对位置有所调整的唯一可能是，某元素_elem[i - 1]严格大于其后继_elem[i]。也就是说，在这种亦步亦趋的交换过程中，重复元素虽可能相互靠拢，但绝对不会相互跨越。由此可知，起泡排序属于稳定算法。

2.1.4 复杂度分析

如图，前r个元素无序，后n-r元素按顺序排列并严格就位。

bubble()算法由内、外两层循环组成。内循环从前向后，依次比较各对相邻元素，如有必要则将其交换。

扫描交换的趟数不会超过O( r )，算法总体消耗时间不会超过O(n *r)次。

故乱序元素仅限于 A[0, $\sqrt{n}$)区间，最坏情况下仍需调用 bubblesort1A ()做$\Omega$( $\sqrt{n}$)次调用，共做$\Omega$(n)次交换操作和$\Omega$(n${}^{\frac{3}{2}}$)次比较操作，因此累计运行$\Omega$(n${}^{\frac{3}{2}}$)时间。
该算法可进一步优化，详见算法设计优化——起泡排序

3. 归并排序

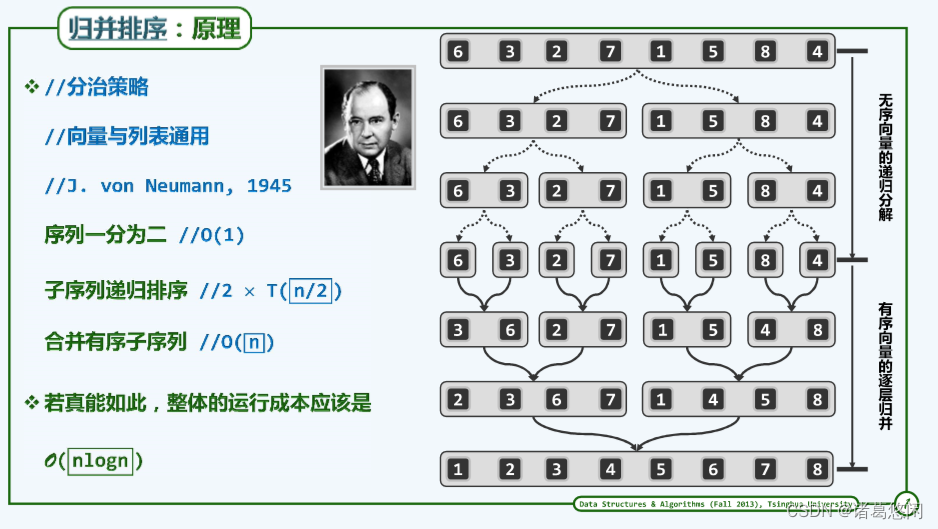
3.1 有序向量的二路归并

二路归并属于迭代式算法。每步迭代中，只需比较两个待归并向量的首元素，将小者取出并追加到输出向量的末尾，该元素在原向量中的后继则成为新的首元素。如此往复，直到某一向量为空。最后，将另一非空的向量整体接至输出向量的末尾。

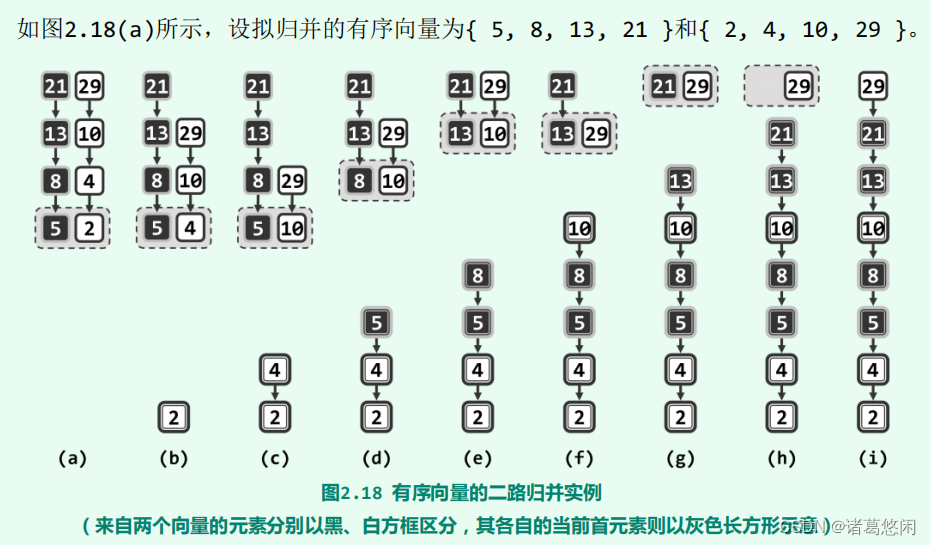
二路归并算法在任何时刻只需载入两个向量的首元素，故除了归并输出的向量外，仅需要常数规模的辅助空间。

3.2 分治策略

算法思想：通过递归调用将二者分别转换为有序向量，即可借助二路归并算法，得到与原向量S对应的整个有序向量

template <typename T> //向量归并排序
void Vector<T>::mergeSort ( Rank lo, Rank hi ) { //0 <= lo < hi <= sizeif ( hi - lo < 2 ) return; //递归基，单元素区间自然有序，否则...int mi = ( lo + hi ) >> 1; //以中点为界 mergeSort ( lo, mi ); //对前半段排序 mergeSort ( mi, hi ); //对后半段排序 merge ( lo, mi, hi ); //归并
}

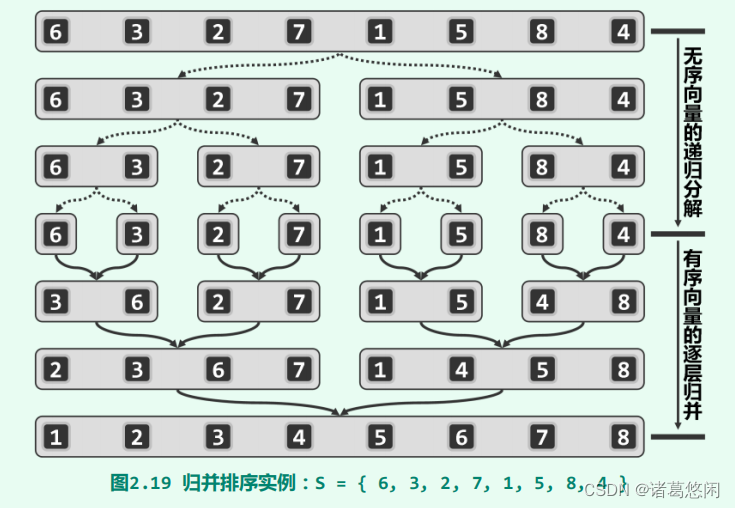
3.3 实例

3.4 二路归并接口的实现

算法思想：创建临时数组B存放数组A的[ lo,mi)元素，数组C指向数组A的[mi,hi)，调用二路归并算法，将有序向量存放在A中。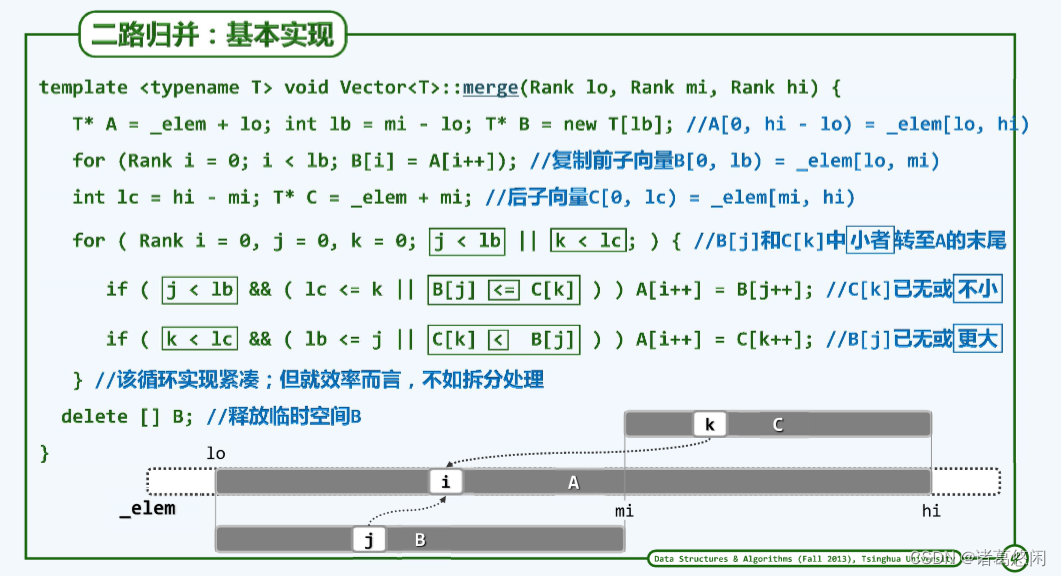

template <typename T> //有序向量的归并
void Vector<T>::merge ( Rank lo, Rank mi, Rank hi ) { //各自有序的子向量[lo, mi)和[mi, hi)T* A = _elem + lo; //合并后的向量A[0, hi - lo) = _elem[lo, hi)int lb = mi - lo; T* B = new T[lb]; //前子向量B[0, lb) = _elem[lo, mi)for ( Rank i = 0; i < lb; B[i] = A[i++] ); //复制前子向量int lc = hi - mi; T* C = _elem + mi; //后子向量C[0, lc) = _elem[mi, hi)for ( Rank i = 0, j = 0, k = 0; ( j < lb ) || ( k < lc ); ) { //B[j]和C[k]中的小者续至A末尾if ( ( j < lb ) && ( ! ( k < lc ) || ( B[j] <= C[k] ) ) ) A[i++] = B[j++];if ( ( k < lc ) && ( ! ( j < lb ) || ( C[k] < B[j] ) ) ) A[i++] = C[k++];}delete [] B; //释放临时空间B
} //递归后得到完整的有序向量[lo, hi)

• 若将后一句中的“C[k] < B[j]”改为“C[k] <= B[j]”，对算法将有何影响？

~~~~     经如此调整之后，虽不致影响算法的正确性（仍可排序），但不再能够保证各趟二路归并的稳定性，整个归并排序算法的稳定性也因此不能保证。 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~                                                  
~~~~     原算法的控制逻辑可以保证稳定性。实际上，若两个子区间当前接受比较的元素分别为B[j]和C[k]，则唯有在前者严格大于后者时，才会将后者转移至A[i++]；反之，只要前者不大于后者（包含二者相等的情况），都会优先转移前者。由此可见，无论是子区间内部（相邻）的重复元素，还是子区间之间的重复元素，在归并之后依然能够保持其在原向量中的相对次序。

• 若将前一句中的“B[j] <= C[k]”改为“B[j] < C[k]”，对算法将有何影响？

当待归并的子向量之间有重复元素时，循环体内的两条处理语句均会失效，两个子向量的首
元素都不会被转移，算法将在此处进入死循环。

3.5 归并时间

二路归并只需线性时间的结论，并不限于相邻且等长的子向量。实际上，即便子向量在物理空间上并非前后衔接（列表），且长度相差悬殊，该算法也依然可行且仅需线性时间。

3.6 排序时间

故：

不足：
路归幵算法 merge()，反复地通过 new 和 delete 操作申请和释放辅助空间。然而实验统计表明，这类操作的实际时间成本，大约是常规运算的 100 倍，故往往成为制约效率提高的瓶颈。
改进点：
可以在算法启动时，统一申请一个足够大的缓冲区作为辅助向量B[]，并作为全局变量为所有递归实例公用；归并算法完成之后，再统一释放。
如此可以将动态空间申请的次数降至O(1)，而不再与递归实例的总数O(n)相关。当然，这样会在一定程度上降低代码的规范性和简洁性，代码调试的难度也会有所增加。

4.综合评价

• 起泡排序最坏情况总需要O($n^2$)
• 归并排序最坏情况下为O(nlogn)

这篇关于【数据结构（邓俊辉）学习笔记】向量05——排序器的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---