本文主要是介绍bite阶段性测试_数据结构,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

解决问题之前我们要了解什么是度,特别是二叉树中的度,和图论中的度的定义是不同的
什么是度:
在图论中,一个节点(或称为顶点)的“度”是指与该节点直接相连的边的数量。度是用来衡量一个节点与其他节点连接紧密程度的指标。在无向图和有向图中,度的概念有所不同:
- 无向图中的度: 对于无向图,一个顶点的度简单地等于连接到该顶点的边的数量。例如,如果一个顶点与三条边相连,那么该顶点的度是3。
- 有向图中的度: 在有向图中,度被分为两种:
-
- 入度(In-degree):入度是指指向该顶点的边的数量。
- 出度(Out-degree):出度是指从该顶点出发指向其他顶点的边的数量。
图论和多(>=2)叉树对 度 的不同定义
二叉树中,节点的度通常是指该节点拥有的子节点的数量,而不是与该节点直接相连的边的数量。因为二叉树是一种特殊的树结构
在图论中,节点的度是指与该节点直接相连的边的数量,而不涉及子节点的概念。因此,图论中的节点度和二叉树中节点的度有所不同
二叉树中,度为0的节点通常指的是叶子节点,即没有子节点的节点,而不是脱离其他顶点的节点
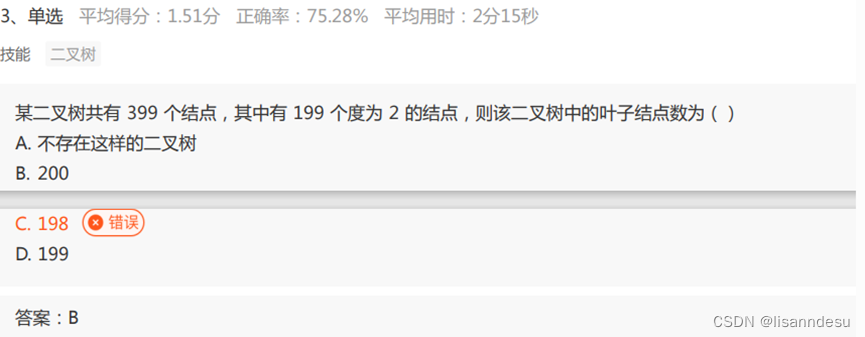
回归本题
树的总节点数 ( n ) 等于所有节点的度数之和再加上1
总节点数 = 1 + 叶子节点数*0 + 度为1的节点数*1 + 度为2的节点数*2
总节点数 = 叶子节点数+度为1的节点数+度为2的节点数
399 = 叶子节点数*0 + 度为1的节点数*1 + 199*2
399 = 叶子节点数+度为1的节点数+度为2的节点数
解得:叶子节点200, 度为一节点0
结论:
总结点数与所有节点度数和关系:
-
-
- 总节点数 = 1 + 叶子节点数*0 + 度为1的节点数*1 + 度为2的节点数*2
- 总节点数 = 叶子节点数+度为1的节点数+度为2的节点数//包有的方程
-
选择排序与堆排序

选择排序是啥,堆排序为啥基于选择排序
选择排序是什么
- 工作原理:选择排序每次从未排序的部分选择最小(或最大)的元素,然后将其放到已排序部分的末尾。
- 特点:在每次迭代中,选择排序只需进行一次交换操作,因此比冒泡排序的交换次数少。
选择排序和冒泡排序区别
选择排序和冒泡排序思想是一样的,只是选择排序优化了实现步骤
选择排序在每次迭代中选择未排序部分的最小(或最大)元素,并将其与当前位置交换,从而减少了交换的次数
Next指向前驱?
通常,prev叫做前驱, next叫做后继节点

筛选法是啥,筛选法建堆是怎么建堆。筛选法作用
筛选法建堆是一种在堆排序算法中用于构建堆的方法。它通常是从数组的中间向前遍历,对每个非叶子节点执行一次筛选操作,使得以该节点为根的子树满足堆的性质。
具体步骤如下:
- 从最后一个非叶子节点开始向前遍历,直到根节点。这些非叶子节点是数组中索引为 n/2 - 1 到 0 的元素,其中 n 是数组的长度。
- 对于每个非叶子节点,执行一次筛选操作(也称为下沉操作):
-
- 比较该节点与其左右子节点的值,找到最大(或最小)的节点。
- 如果子节点的值大于(或小于)该节点的值,则交换两者的位置。
- 继续递归向下进行,直到满足堆的性质为止。
通过这样的操作,可以将一个无序的数组构建成一个堆,使得堆的根节点具有最大(或最小)的值,且满足堆的性质。
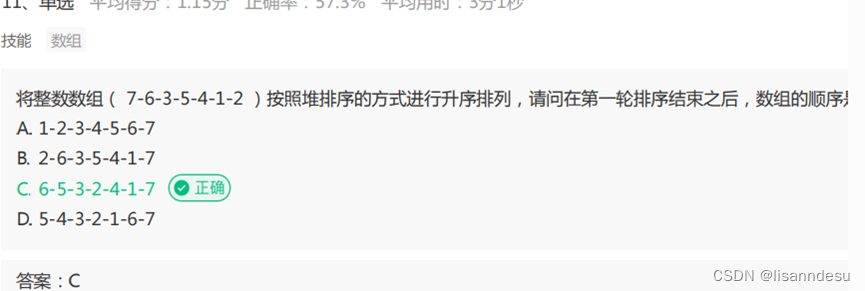
堆排序怎么排来着
上述筛选法建堆排序

六大排序稳定性?
- 冒泡排序(Bubble Sort):稳定。
- 选择排序(Selection Sort):不稳定。在选择最小元素的过程中可能破坏相等元素的相对位置。
- 插入排序(Insertion Sort):稳定。相等元素的相对位置在排序前后不变。
- 快速排序(Quick Sort):不稳定。对相等元素可能会进行交换,导致相对位置变化。
- 归并排序(Merge Sort):稳定。在合并过程中,相等元素的相对位置保持不变。
- 堆排序(Heap Sort):不稳定。在堆化的过程中可能会交换相等元素的位置,导致不稳定性。
只有快排和选择排序堆排序不稳定
插入和归并都稳定
为啥选择和冒泡基本思路相同,选择却不稳定?
举个例子,考虑序列 [2a, 3, 2b],其中元素 2a 和 2b 相等,但是它们的相对位置是不同的。如果选择排序先选中 2a,然后将其移动到已排序序列的末尾,那么排序后的序列可能变为 [3, 2b, 2a],导致相对位置的改变,从而不满足稳定性的要求。
--------------------------------------------------------------------------
快排
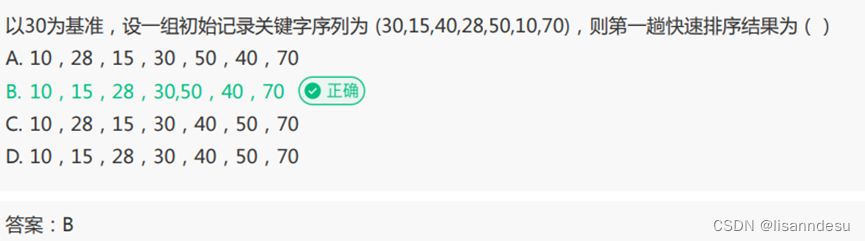
快排升序,左先走/右先走?为什么?
为啥碰到10?
当升序时,普通快排一定要右先走来保证相遇点为小于等于key的点
反之,降序左先走
普通快排code
void QuickSort1(int* a, int left, int right)
{
// 区间只有一个值或者不存在就是最小子问题
if (left >= right)
return;
// 小区间选择走插入,可以减少90%左右的递归
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);
}
else
{
int begin = left, end = right;
// 100 200,注意的是left不一定是0
// 选[left, right]区间中的随机数做key
//int randi = rand() % (right - left + 1);
//randi += left;
//Swap(&a[left], &a[randi]);
// 三数取中
int midi = GetMidi(a, left, right);
//printf("%d\n", midi);
Swap(&a[left], &a[midi]);
//PrintArray(a+left, right-left+1);
int keyi = left;
while (left < right)
{
// right先走,找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
// left再走,找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
// [begin, keyi-1]keyi[keyi+1, end]
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
}
挖坑法

前后指针法

-------------------------------------------------------------------------------
归并排序code
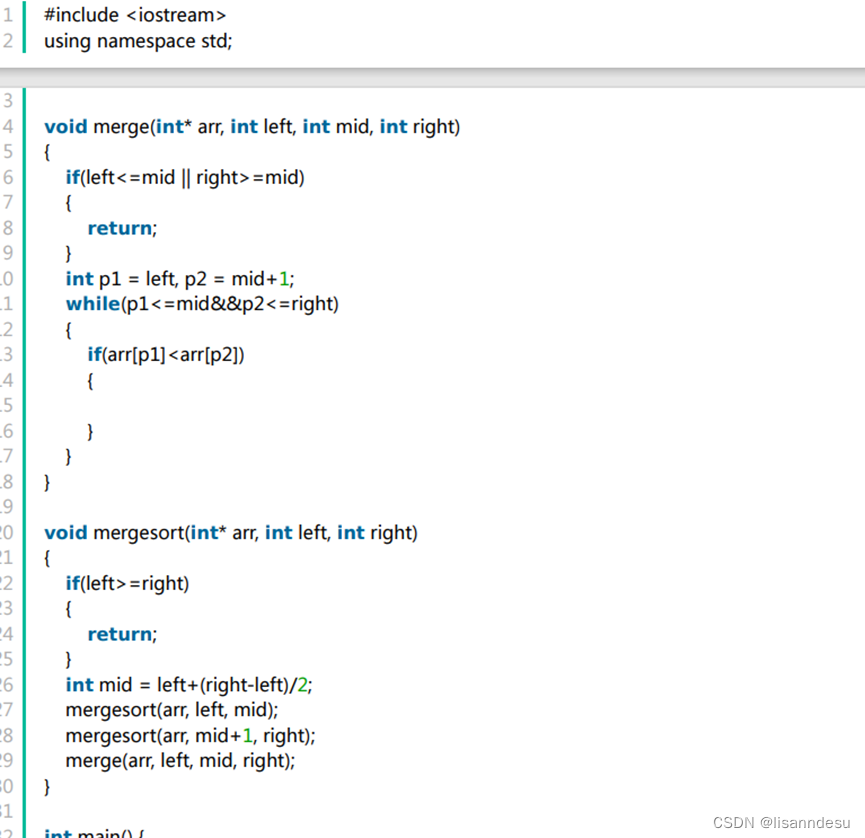
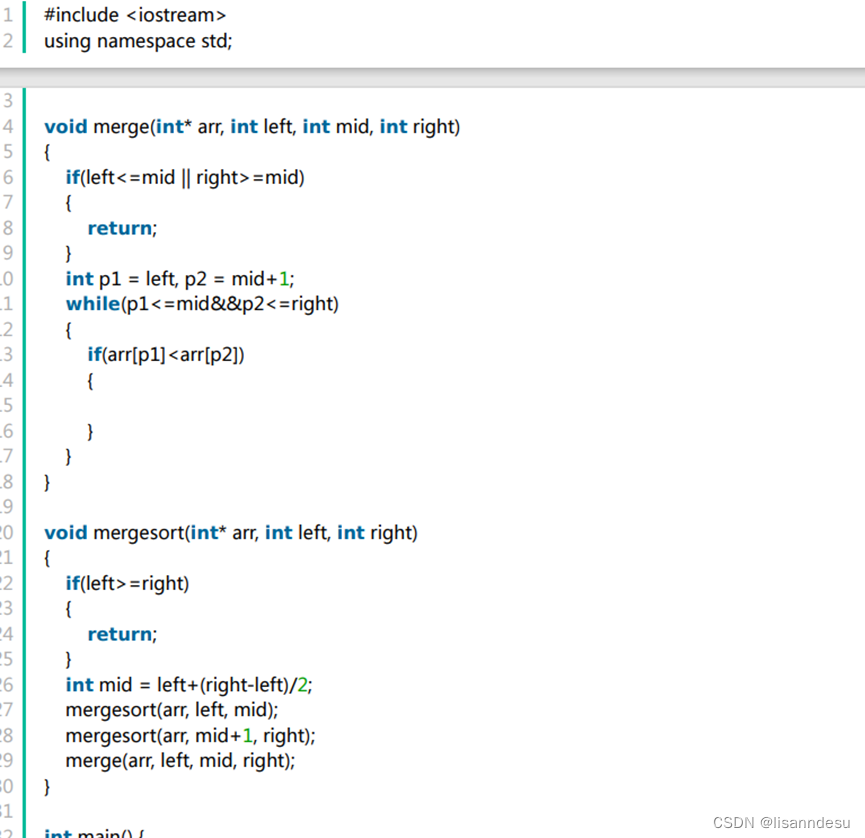
大体思路没问题,还差一点没写完不影响理解
这篇关于bite阶段性测试_数据结构的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







![业务中14个需要进行A/B测试的时刻[信息图]](https://img-blog.csdnimg.cn/img_convert/aeacc959fb75322bef30fd1a9e2e80b0.jpeg)