本文主要是介绍函数定义域和值域,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
定义域和值域
1. 函数的定义
函数的定义:一般的,在一个变化过程中,假设有两个变量 x x x, y y y,如果对于任意一个 x x x 都有唯一确定的一个 y y y 和它对应,那么就称 x x x 是自变量, y y y 是 x x x 的函数。 x x x 的取值范围叫做这个函数的定义域,相应 y y y 的取值范围叫做函数的值域。
y = f ( x ) y=f(x) y=f(x)
2. 定义域
定义域(domain of definition)指自变量 x x x 的取值范围,是函数三要素(定义域、值域、对应法则)之一,对应法则的作用对象。求函数定义域主要包括三种题型:抽象函数,一般函数,函数应用题。
定义一:设 x x x, y y y 是两个变量,变量 x x x 的变化范围为 D D D,如果对于每一个数 x ∈ D x \in D x∈D,变量 y y y 遵照一定的法则总有确定的数值与之对应,则称 y y y 是 x x x 的函数,记作 y = f ( x ) y=f(x) y=f(x), x ∈ D x \in D x∈D, x x x 称为自变量, y y y 称为因变量,数集 D D D 称为这个函数的定义域。
3. 值域
值域,数学名词,在函数经典定义中,函数值因自变量改变而改变的取值范围叫做这个函数的值域,在函数现代定义中是指定义域中所有元素在某个对应法则下对应的所有的象所组成的集合。如: f ( x ) = x f(x)=x f(x)=x,那么 f ( x ) f(x) f(x) 的取值范围就是函数 f ( x ) f(x) f(x) 的值域。
4. 垂线检验
函数的图像只有一点比较特殊:它必须满足垂线检验,只要满足垂线检验那么图像可以散落四处:这里有一部分,那里有一部分,或有一条垂直渐近线, 或者随心所欲地在各处散落任意个不连续的点。换而言之就是一个函数的图像可以由多个部分组成的,所以对于函数是否满足条件的要求是不多的 。
那么什么是垂线检验?
函数的图像是所有坐标为 ( x , f ( x ) ) (x,f(x)) (x,f(x)) 的点的集合。我们以某个实数开始,如果 x x x 在定义域中,则在坐标中画出点 ( x , f ( x ) ) (x,f(x)) (x,f(x)),这个点在 x x x 轴的点 x x x 的垂直线上,距离 x x x 轴高度为 f ( x ) f(x) f(x)。如果 x x x 没有在定义域中,则坐标中不存在该点。现在,对于每一个实数 x x x,我们重复这一个过程,从而构造出函数的图像。
垂线检验的作用?垂直检验用于判断画出的图形是否是函数的图像。它的思想是:不可能有两个点有相同的 x x x 坐标。换句话说,在图像上没有两个点会落在相对于 x x x 轴的同一条垂线上。要不然,我们如何知道在点 x x x 上的两个或多个坐标点中,哪一个坐标点的高度( y y y 值)对应了 f ( x ) f(x) f(x) 的值呢。
5. 奇偶性
奇偶性是函数的基本性质之一,下面理解以下奇偶性的定义,还会举几个例子。
(1) 一般地,如果对于函数 f ( x ) f(x) f(x) 的定义域内任意一个 x x x,都有 f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x),那么函数 f ( x ) f(x) f(x) 就叫偶函数。
(2) 一般地,如果对于函数 f ( x ) f(x) f(x) 的定义域内任意一个 x x x,都有 f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x),那么函数 f ( x ) f(x) f(x) 就叫奇函数。
(3) 偶函数的图像以函数坐标系的 y y y 轴对称,基函数的图像以函数坐标系的原点( O O O)对称,如下图 1-10 为偶函数,1-11 为奇函数。
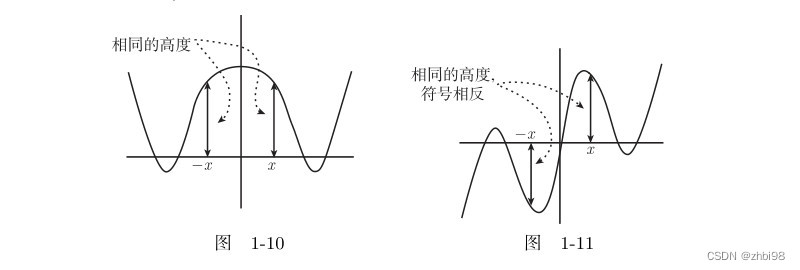
函数 y = x 2 y=x^2 y=x2 无论 x x x 的值为正还是为负由于平方的关系最终 y y y 的值都是相同的,所以 y = x 2 y=x^2 y=x2 就是偶函数(根据定义 f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x))。函数 y = x 3 y=x^3 y=x3 当 x x x 的值为正时最终 y y y 值也为正,当 x x x 的值为负时最终 y y y 为负,不过值得大小是相同的,只是符号不同所以 y = x 3 y=x^3 y=x3 就是奇函数(根据定义 f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x),意思是说将负值代入函数得到的结果和正值代入函数得到的结果直接加上负号后得到的结果是相同的)。
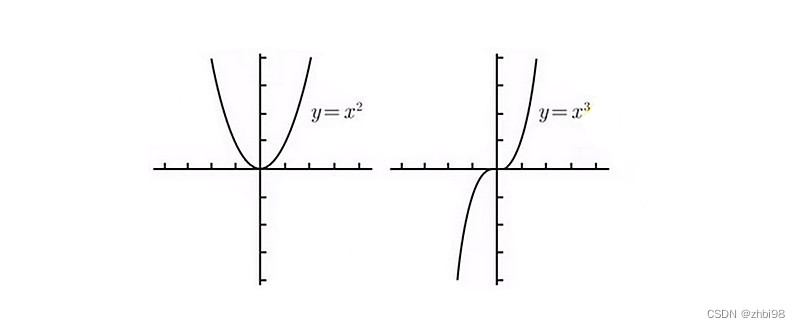
从上图也可以看出 y = x 2 y=x^2 y=x2 图像以 y y y 轴对称, y = x 3 y=x^3 y=x3 的图像以原点对称。
反函数
如果一个函数与另一个函数相反,那么这个函数是另一个函数的反函数,这两个函数在图像上是相反的,简单地说, y = f ( x ) y=f(x) y=f(x) 是 y y y 关于自变量 x x x 的函数,如果存在一个函数 g g g,使得 g ( y ) = g ( f ( x ) ) = x g(y)=g(f(x))=x g(y)=g(f(x))=x 那么 x = g ( y ) x=g(y) x=g(y) 就是 y = f ( x ) y=f(x) y=f(x) 的反函数,记作 x = f − 1 ( y ) x=f^{-1}(y) x=f−1(y)。
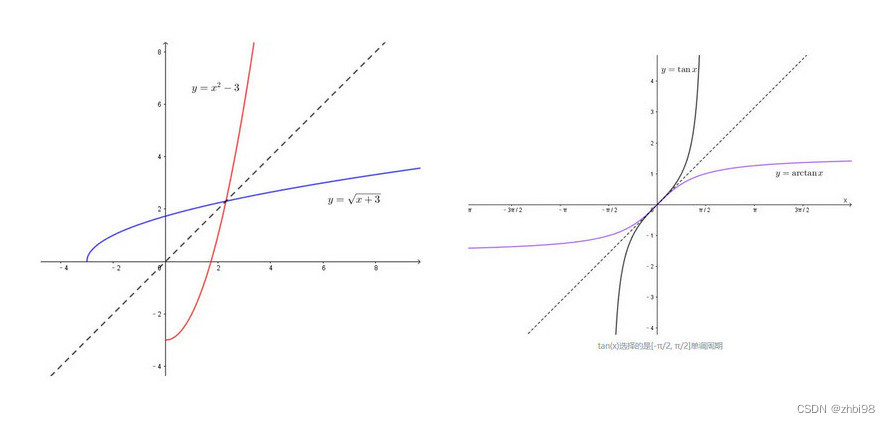
当我们需要求一个函数的反函数,我们只需要将自变量和因变量置换,然后求出相应的函数即可。
这篇关于函数定义域和值域的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





