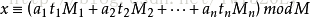【ACM】中国剩余定理（CRT）

本文主要是介绍【ACM】中国剩余定理（CRT），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

中国剩余定理是求解一次线性同余方程组的方法。

中国剩余定理：
假设整数m1,m2, … ,mn两两互素，则同余方程组

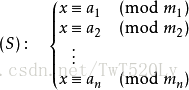
有整数解。
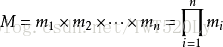
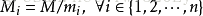
设 是m1,m2,m3…mn的乘积，并设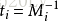 是除了mi以外的n-1个整数的乘积。
设是Mi模mi的逆元（数论中的倒数）。

那么在模M下的解是唯一的。

模板代码如下：

void Extend_Euclid(int a,int b,int& x,int& y)
{if(b == 0){x = 1;y = 0;return; //表示程序退出，但是没有返回值}Extend_Euclid(b,a%b,x,y);int temp = x;x = y;y = temp - (a/b) * y;
}int CRT(int a[],int m[] ,int n)
{int M=1;int ans = 0;for(int i=1;i<=n;i++)M *= m[i];   for(int i=1;i<=n;i++){int x,y;int Mi = M/m[i];Extend_Euclid(Mi,m[i],x,y); // 求逆元ans = (ans + a[i]*Mi*x) % M;}if(ans<0)ans += M;return ans;
}

这篇关于【ACM】中国剩余定理（CRT）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---