本文主要是介绍【静态分析】静态分析笔记09 - 污点分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考:
【课程笔记】南大软件分析课程—16课时完整版 - 知乎
-------------------------------------------------------------------------------
1. 信息流安全
访问控制:关注信息访问。
信息流安全:关注信息传播。
信息流:x->y表示x的值流向y。
信息等级:对不同变量进行分级,即安全等级,H-高密级,L-低密级。
安全策略:非干涉策略,高密级变量H的信息不能影响(流向)低密级变量L。
2. 保密性和完整性
保密性—信息泄露,读保护;
完整性—信息篡改,写保护。
完整性错误类型:命令注入、SQL注入、XSS攻击... 都属于注入错误。
3. 显示流和隐藏信道 - Explicit Flows and Covert Channels
显示流:直接的数值传递。由于显示流能泄露更多信息,所以本课程关注显示流的信息泄露。
隐式信息流—侧信道:程序可能会以一些意想不到的方式泄露数据。
// Eg1 隐式流
if (secret_H < 0) public_L = 1;
else Public_L = 0;
// Eg2 终止信道
while(secret_H < 0) { ... };
// Eg3 时间信道
if (secret_H < 0)for (int i = 0; i< 1000000; ++i) { ... };
// Eg4 异常
if (secret_H < 0)throw new Exception("...");
// Eg5 如果访问数组越界,则可以推断secret可以为负数
int sa_H[] = getSecretArray();
sa_H[secret_H] = 0;
信道指的是传递信息的机制
covert channels:原本目的不是为了传递信息的信道。
4. 污点分析
说明:使用最广的信息流分析技术,需将程序数据分为两类,把感兴趣的数据标记为污点数据。
(1)概念
保密性:Source是秘密数据,sink是泄露点,信息泄露漏洞。
x = getPassword(); // source
y = x;
log(y); // sink
完整性:Source是不可信数据,Sink是关键计算,注入漏洞。
x = readInput(); // source
cmd = "..." + x;
execute(cmd); // sink
(2)污点分析
定义:关注的是,污点数据是否能流向sink点。或者说,sink点处的指针指向哪些污点数据。
TA/PTA对比:污点分析与指针分析,一个是污点数据的流向,一个是抽象对象的流向。可把污点数据看作是对象,借助指针分析来实现污点分析。
标记:ti表示调用点i返回的污点数据,指针集就包含普通对象+污点数据。

输入:source(返回污点数据的函数),sink(违反安全规则的函数)
输出:TaintFlows—<ti, m>,表示ti这个污点数据会流向m函数,污点数据和sink函数这个pair的集合就是TaintFlows。
规则:主要规则不变,关键是Sources和Sink调用的处理。
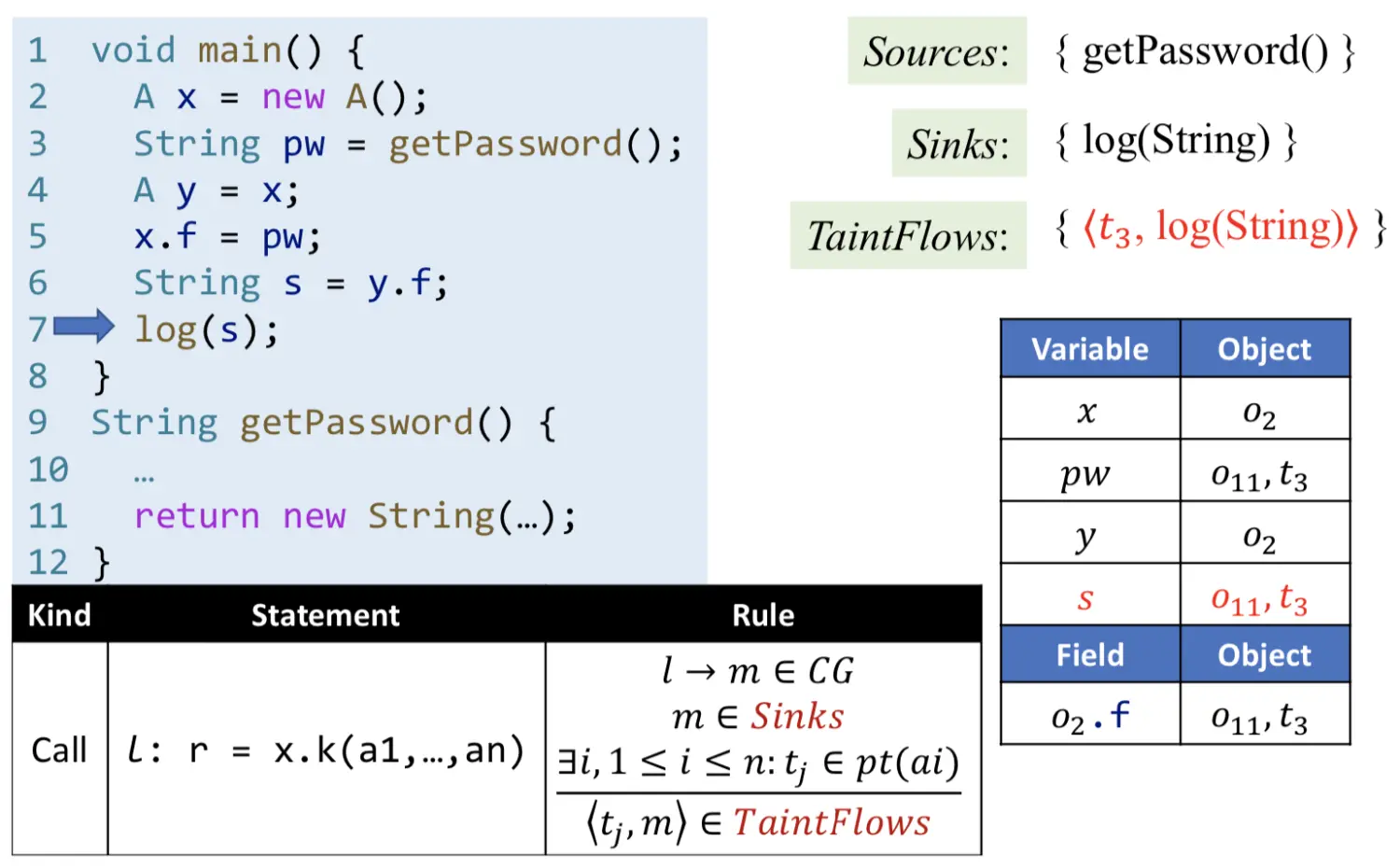
Sources:对于产生污点源的函数调用m,将返回值标记为污点值tl,并更新接收变量r的指向。Sink:对于Sink函数m,若所传参数的指向集包含污点tj,则将<tj, m>加入TaintFlows。


示例:第3行产生新对象o11的同时,产生的污点数据t3;最终指针分析发现,t3会流向sink函数log()。
问答:
实现分析器用到:分析Java用Soot/WALA;分析C++用LLVM。
隐藏信道的论文:Implicit Flows: Can’t Live With ‘Em, Can’t Live Without ‘Em
这篇关于【静态分析】静态分析笔记09 - 污点分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



