第四篇：深入探索Python数据结构：打基础，建高楼

本文主要是介绍第四篇：深入探索Python数据结构：打基础，建高楼，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

深入探索Python数据结构：打基础，建高楼

在这里插入图片描述

1 引言

在编程世界里，数据结构的重要性不亚于建筑学中的基础工程。正如一栋大厦需要坚实的基础来支撑其庞大的结构，软件程序也需要合理的数据结构来保证其性能和稳定性。对于使用Python这一高级编程语言的开发者来说，深入理解其内建的数据结构是提升代码效率与质量的关键。

1.1 为什么要深入了解Python数据结构

数据结构是计算机存储、组织数据的方式。它不仅决定了数据的存储方式，还影响着数据的检索和更新效率。在Python中，高效的数据结构能够使得程序更加快速和灵活，因此，对数据结构的深入了解能够帮助我们更好地解决实际问题。

1.2 数据结构在Python编程中的重要性

Python提供了多种内建的数据结构，如列表（List）、元组（Tuple）、字典（Dictionary）和集合（Set），每种结构都有其特定的应用场景和优势。选择正确的数据结构可以大幅度提高程序的执行效率。例如，在进行大量包含唯一元素的快速查找操作时，集合（Set）会比列表（List）更加高效。

让我们涉足数学领域来更详细地理解这个概念。复杂度分析是衡量算法效率的数学工具，它用大O符号（ $O$ ）来描述算法的性能或复杂度。例如，列表的索引操作是常数时间的，表示为 $O (1)$ ，而对于列表的排序操作，其时间复杂度通常是 $\log n)$ ，这意味着它的运行时间随着列表大小的增加而增加，但增加的速度慢于列表大小的线性增长。数学公式和模型为我们提供了一个强大的工具，用于推导和验证这些操作的性能，这也是我们在本系列文章中将反复回到的主题。

举一个具体的例子：考虑一个场景，在这个场景中，你需要存储一系列学生的成绩，并对它们进行多种操作，如添加新成绩、删除成绩、查找特定学生的成绩等。如果选择使用列表（List）来存储这些成绩，那么在列表中查找特定学生的成绩所需的时间将与列表的长度成正比；而如果使用字典（Dictionary），每次查找的时间几乎都是常数时间，这在有大量学生数据时的性能差异是显著的。

在接下来的章节中，我们将深入探讨每种数据结构的内部工作原理及其在实际编程中的应用案例。我们将通过详细的操作示例、性能分析图表和实际编程问题的解决方案，来展示如何根据具体需求选择和使用合适的数据结构。

总之，无论您是数据科学家、Web开发人员还是自动化测试工程师，深入了解并合理利用Python中的数据结构将是您技能库中的一项宝贵财富。追随我们的脚步，让我们一起开始这趟精彩的探索之旅吧。

在这里插入图片描述

2 列表（List）

2.1 基本概念和创建方法

在Python的世界中，列表（List）是最常用且最灵活的数据结构之一。列表可以被理解为一个容器，它能够按顺序存储一个序列的值。这些值可以是任何类型的数据，包括数字、字符串、甚至是其他列表（即嵌套列表）。

列表的定义

数学上，我们可以将列表视为一个有序集合，其中的元素可以通过整数索引来访问。这种有序性可以用数学公式 $L i s t [i]$ 来表示，其中 $i$ 是从0开始的索引值。

在Python中，列表定义为：

List = [item1, item2, item3, ..., itemN]

列表的长度（即元素的数量）是可变的，并且列表中的元素可以随时被修改。这与某些其他语言中的数组概念相似，但Python的列表具有更多的灵活性和功能。

如何创建列表

创建列表的方法很简单。你可以用一对方括号来初始化一个空列表，或者在方括号中放入一些初始值：

# 创建一个空列表
empty_list = []# 创建一个包含某些元素的列表
fruits = ['apple', 'banana', 'cherry']

列表也可以通过列表推导式（list comprehension）来创建，这是一种优雅且具有Python特色的方式，能够基于某些规则或现有的列表创建一个新列表：

# 使用列表推导式创建一个列表，包含0至9的平方
squares = [x**2 for x in range(10)]

在深入探索列表时，我们会发现列表不仅仅是一个简单的容器。在计算机科学的角度来看，Python的列表可以被看作是一个动态数组。动态数组的优点是可以动态地调整其大小，与静态数组（大小固定的数组）相比，Python的列表无需预先声明容量大小，它会根据需要自动扩张或收缩。

数学模型可以帮助我们理解这种行为。考虑列表的内存分配模型，当你添加元素到列表时（例如，使用 append 方法），如果当前的内存块没有足够的空间，列表会重新分配一个大约为当前大小两倍的内存块。这个过程中，已有元素被复制到新的内存块，然后添加新的元素。这种行为的平均时间复杂度可用 $O (1)$ 表示，但实际的单次增长操作可能达到 $O (n)$ ，其中 $n$ 是列表的当前长度。

在接下来的章节中，我们将深入探讨列表的操作方法，如何高效地使用列表，并且通过可视化示例来帮助我们更直观地理解列表的结构和操作。通过这些深入的讲解与实际编程实例，不仅能够增强我们对列表的认知，还能够提升我们使用这一强大数据结构的能力。

2.2 列表的操作

在深入了解Python的列表之前，让我们先回顾一下，列表在Python中的定义是一个可变的序列类型。这意味着列表不仅可以存储一个序列的元素，而且还可以在程序运行时动态地添加、删除或更改其内容。

增加元素（append, insert）

Python允许以多种方式向列表中添加元素。最常见的方法是使用 append() 方法，它向列表的末尾添加一个元素。数学上，假设列表 $L$ 的长度为 $n$ ，当我们执行 L.append(e) 时，我们正在执行以下操作：

$L_{new} = L_{old} \cup \{e\}$

其中 $e$ 是要添加的新元素。此操作的时间复杂度为 $O (1)$ ，因为它是在列表的末尾添加元素。

numbers = [1, 2, 3]
numbers.append(4)  # numbers 现在是 [1, 2, 3, 4]

insert() 方法则允许在列表中指定位置插入一个元素。如果我们需要在位置 $i$ 插入元素 $e$ ，则数学上的操作可以描述为：

$L_{new}[j] = \begin{cases} L_{old}[j] & \text{for } j < i \\ e & \text{for } j = i \\ L_{old}[j-1] & \text{for } j > i \end{cases}$

而这个操作的平均时间复杂度为 $O (n)$ ，因为可能需要移动 $i$ 之后的所有元素。

numbers.insert(2, 99)  # numbers 现在是 [1, 2, 99, 3, 4]

删除元素（remove, pop）

与添加元素类似，列表也提供了几种删除元素的方法。remove() 方法可以删除列表中出现的第一个匹配元素。如果列表中没有这样的元素，则会抛出一个异常。数学表示为：

$L_{new} = L_{old} - \{e\}$

其中 $e$ 是要删除的元素。这个操作的平均时间复杂度也是 $O (n)$ ，因为在找到并删除元素后可能需要移动后续所有元素。

numbers.remove(99)  # numbers 现在是 [1, 2, 3, 4]

pop() 方法则删除并返回列表中的一个指定位置的元素。如果没有指定位置，它将默认删除并返回列表中的最后一个元素。这个操作在最好的情况下（删除列表末尾的元素）时间复杂度为 $O (1)$ ，在最坏的情况下（删除列表开头的元素）时间复杂度为 $O (n)$ 。

last_item = numbers.pop()  # last_item 是 4，numbers 现在是 [1, 2, 3]

列表排序和反转

列表的 sort() 方法可以将列表中的元素进行就地升序排序，也可以接受一个 reverse=True 的参数来进行降序排序。这个方法使用的是TimSort算法，一个混合的排序算法，其平均时间复杂度为 $\log n)$ 。

numbers = [3, 1, 4, 1, 5, 9, 2]
numbers.sort()  # numbers 变为 [1, 1, 2, 3, 4, 5, 9]

如果你仅仅需要反转列表中元素的顺序，使用 reverse() 方法将比排序要高效得多，因为 reverse() 方法的时间复杂度为 $O (n)$ 。

numbers.reverse()  # numbers 变为 [9, 5, 4, 3, 2, 1, 1]

列表的排序和反转操作是编程中常见的需求，并且其高效的实现是Python作为一门高级语言的又一体现。通过这些方法，我们可以轻松地对数据进行准备，以便进行进一步的分析或处理。

在本章节中，我们已经详细讨论了列表的基本操作，包括如何添加、删除元素以及如何排序和反转列表。了解这些操作不仅有助于编写有效的程序，而且通过数学表示也加深了我们对这些操作的基本概念的理解。在下一章节中，我们将探讨列表推导式，这是Python中强大的功能之一，它可以帮助我们以简洁和高效的方式生成列表。

2.3 列表推导式

在深入Python的世界中，列表推导式是一种简洁且富有表达力的构建列表（List）的方法。它不仅提高了代码的可读性，而且在执行速度上往往优于传统的循环方法。那么，列表推导式具体是如何工作的呢？让我们一探究竟。

列表推导式在Python中可以用单行的简洁语法来代替多行循环处理过程。基本的形式如下：

[表达式 for 变量 in 可迭代对象 if 条件表达式]

这里的“表达式”是指一个Python表达式，该表达式通常依赖于循环变量；“变量”是循环变量；“可迭代对象”是任何Python的可迭代对象；“条件表达式”则用于过滤那些不满足条件的元素。

举一个简单的例子，若我们想要得到一个包含平方数的列表，使用传统的循环方式，我们会写出如下代码：

squares = []
for x in range(10):squares.append(x**2)

而使用列表推导式，我们可以将同样的操作简化为一行代码：

squares = [x**2 for x in range(10)]

但是，列表推导式的真正威力在于它能够优雅地处理更加复杂的逻辑。例如，如果我们要生成一个新列表，包含某个列表中非负数的平方，我们可以添加一个条件表达式：

original = [-4, -2, 0, 2, 4]
squares = [x**2 for x in original if x >= 0]

列表推导式还支持多层嵌套，这使得它们能够在复杂数据结构的处理中发挥巨大作用。比如，我们要计算两个列表中所有数字对的和，只要它们不相等，我们可以写出如下表达式：

a = [1, 2, 3]
b = [3, 4, 5]
pairs_sum = [x + y for x in a for y in b if x != y]

在数学上，这等同于构建一个笛卡尔积，然后应用条件过滤。如果我们将它写成集合表示，可以表示为：

$\times B = \{(x,y) \mid x \in A \land y \in B \land x \neq y \}$

$\times B) = \{x + y \mid (x,y) \in A \times B\}$

其中， $A$ 和 $B$ 是集合，而 $\times B$ 表示的是从集合 $A$ 和集合 $B$ 中分别取出元素组成的有序对集合，满足条件 $\neq y$ 。

在处理更加复杂的数据结构时，列表推导式提供了一种极为强大的工具。例如，如果我们有一个矩阵（二维列表），我们希望“转置”它，即交换其行和列，使用传统方法可能需要使用嵌套循环，而使用列表推导式则可以简洁地完成：

matrix = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]
transposed = [[row[i] for row in matrix] for i in range(len(matrix[0]))]

这里，我们使用了嵌套的列表推导式，外层循环遍历矩阵的列索引，内层循环遍历矩阵的行。这就为我们提供了一个按列取值的机制，最终获得一个按照列索引组织数据的新列表。

总而言之，列表推导式是Python中处理列表操作的一个强大工具，通过精简的语法能够完成复杂的列表处理任务。它不仅提高了代码的可读性，还往往能够带来性能上的提升。正如建筑师通过精心设计打造宏伟建筑一样，Python程序员可以利用列表推导式在数据结构的世界中构建出优雅而高效的解决方案。

在我们的数据结构之旅中，掌握列表推导式就像在手中握有一把锐利的工具，无论是处理数据分析中的数列转换，还是进行日常编程中的快速列表生成，它都能帮我们极大地提高效率与编码的乐趣。在未来的章节中，我们还将探索Python中其他数据结构的推导式，比如字典推导式，它们同样能够为我们的编程实践增添强大的动力。

2.4 高级特性

在探讨Python列表（List）的基本操作之后，我们来深入其高级特性，这些特性将使得列表操作更加高效和强大。列表的高级特性包括切片操作和嵌套列表，这些特性在处理大型数据集时尤其有用。

列表的切片操作

列表的切片操作使得我们能够灵活地访问列表的一部分元素。切片操作可以用数学公式来表达：

$S [i : j : k]$

其中， $S$ 表示源列表， $i$ 是切片开始的索引， $j$ 是切片结束的索引，而 $k$ 是步长。需要注意的是，切片操作创建的是原列表的一个副本，原列表不会被修改。

例如，我们有一个列表 L = [0, 1, 2, 3, 4, 5]，我们可以进行如下切片操作：

# 从索引1到索引4取元素
sublist = L[1:5]
# 输出: [1, 2, 3, 4]

这里的切片操作等价于公式 $L [1 : 5 :]$ ，其中默认步长是1。

如果我们想每隔一个元素取一个值，可以设置步长为2：

# 从开始到结束每隔一个元素取一个元素
sublist = L[::2]
# 输出: [0, 2, 4]

这可以表示为 $L [0 : l e n (L) : 2]$ 。

使用负数作为步长可以实现列表的反转：

# 列表反转
reversedL = L[::-1]
# 输出: [5, 4, 3, 2, 1, 0]

这个操作相当于 $L [- 1 : - (l e n (L) + 1) : - 1]$ ，它从列表的末尾开始，以-1的步长向前遍历。

嵌套列表

嵌套列表是指列表内部的元素也是列表，这允许我们构建类似于矩阵的数据结构。例如：

matrix = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]

我们可以使用双重索引访问嵌套列表中的元素，例如访问元素6，我们可以用 matrix[1][2]。

而嵌套列表的遍历通常会使用嵌套的循环：

for row in matrix:for item in row:print(item)

在数学上，我们可以将嵌套列表视为一个矩阵 $M$ ，其中 $M_{i,j}$ 表示位于第 $i$ 行和第 $j$ 列的元素。那么，对于上面的 matrix， $M_{1,2}$ 的值就是6。

嵌套列表甚至可以用来表示更高维度的数据结构。例如，你可以有一个3维列表，它可以表示为一个立方体的形式，其中每个元素的位置可以用三个索引来描述。

列表的这些高级特性，特别是切片和嵌套列表，使得Python在科学计算和数据分析中成为一种强大的工具。通过掌握这些特性，你可以编写出更加简洁和高效的代码。

2.5 可视化实例

在Python编程的世界中，列表（List）是最常用的数据结构之一，提供了一系列灵活的操作来处理数据集合。如同代数中的向量概念，它能够以有序的方式存储条目，并允许我们通过索引来访问这些条目。为了更好地理解列表的操作，让我们借助可视化的实例来深入探究。

列表的图形表示

想象列表就像一列盒子，每个盒子可以存放不同类型的数据，如整数、字符串或者其他对象。在数学表示中，我们可以将列表 ( L ) 表示为：

$L = [a_1, a_2, a_3, ..., a_n]$

其中， $a_i )$ 表示列表中的第 ( i ) 个元素，( n ) 是列表的长度。例如，一个包含整数的列表可以是：

$L = [3, 1, 4, 1, 5, 9, 2, 6]$

这个列表中有8个元素，因此它的长度 ( n = 8 )。

列表操作的可视化

接下来，我们可视化一些基本操作，例如添加元素和删除元素。

添加元素：使用 append() 方法将一个新元素添加到列表的末尾。如果我们想将元素 ( 7 ) 添加到上面的列表 ( L )，数学化的表达方法是：

$L_{new} = L_{old} \cup \{7\}$

在Python中，它看起来像：
```
L.append(7)
```
可视化表达，列表 ( L ) 现在将包含一个额外的盒子，存有元素 ( 7 )。
删除元素：使用 pop() 方法来删除并返回列表中的一个指定位置上的元素。例如，删除第三个元素：

$L_{new} = L_{old} - \{a_3\}$

或者在Python中：
```
L.pop(2)  # Indexing starts at 0, so 2 represents the third element
```
可视化来看，列表 ( L ) 的第三个盒子将被取出，盒子中的值（在我们的例子中是 ( 4 )）将不再存在于列表中。

排序操作的可视化

排序是另一个常见的列表操作。如果我们对列表 ( L ) 进行排序：

$L_{sorted} = sort(L)$

在Python里，我们可以简单地调用 sort() 方法：

L.sort()

排序后的列表 ( L_{sorted} ) 将按照升序排列其元素。可视化的表达，盒子被重新排列，使得每个盒子中的数值按从小到大的顺序显示。

这些操作的可视化有助于我们理解列表是如何被修改的，并且也让我们能够更容易地推广到更复杂的数据结构操作。例如，考虑列表的切片操作，我们可以用数学公式表示为：

$L_{slice} = L[i:j]$

在Python中，它被表示为：

L_slice = L[i:j]

其中，( i ) 和 ( j ) 分别是切片的起始和结束索引。在这个方面，可视化帮助我们看到了原列表 ( L ) 中的一个子集是如何被创建的。

通过以上的可视化实例，我们可以更加直观地理解列表的操作，并且将这些概念应用到实际的编程问题中。列表是一个强大的工具，无论是在数据处理、算法设计还是日常的编程任务中，它都扮演着不可或缺的角色。通过熟练地使用列表和理解其背后的数学原理，我们可以构建更有效和更可靠的Python程序。

在这里插入图片描述

3 元组（Tuple）

3.1 基本概念和创建方法

在Python的世界里，元组（Tuple）是一种不可变的序列类型，它允许我们存储一个有序的元素集合。正因为它的不可变性，元组在创建后不可以被修改，这为数据的安全性提供了一定程度的保障。可以将元组想象成一本写定了的书籍，页数和内容固定，阅读者可以随意翻阅，但无法添改其中的文字。

创建元组的数学定义

数学上，元组可以定义为有序的元素对集合，表示为 $T = (a_1, a_2, ..., a_n)$ ，其中每个元素 $a_i$ 可以是任意类型，且 $n$ 表示元组的长度。在Python中，我们通过将一系列用逗号分隔的值放置在圆括号 $()$ 中来创建元组，例如：

my_tuple = (1, 2, 3)

创建元组的方法

创建元组的基本方法非常直观和灵活。下面是几种不同的创建方法举例：

直接指定元组中的元素，如前文所示。
使用一个可迭代对象，通过内置的 tuple() 函数转换创建，比如从列表转换：
```
list_example = [1, 2, 3]
tuple_from_list = tuple(list_example)
```
利用元组的不可变性来创建包含重复元素的元组，使用数学公式的语言，可以用笛卡尔积来描述该过程：

$T_{repeated} = t_1 \times t_2 \times ... \times t_n$

其中每个 $t_i$ 是一个单一的重复元素。在Python中，这可以通过乘法操作来简化实现：
```
repeated_tuple = ('Python',) * 3
```
单元素元组的创建，需要在元素后添加逗号以避免与数学中的小括号混淆：
```
single_element_tuple = ('Solo',)
```

无括号的元组

在Python中，括号并不是定义元组的必要条件，只要逗号存在，即便省略了括号，Python解释器也能识别出元组的存在。例如：

a = 1, 2, 3

在上面的例子中，a 确实是一个包含三个整数的元组，这是元组的“隐式”创建方法。

空元组和单元素元组

空元组是不含任何元素的特殊元组，可以通过空的圆括号来创建：

empty_tuple = ()

对于单元素元组，如果省略了逗号，则括号会被解释为数学公式中的普通括号，因此为了避免歧义，单元素元组的创建需要跟随一个逗号：

single_element_tuple = (42,)

元组的不可变性

这种数据结构的不可变性意味着一旦元组被创建，它的内容和大小将不能改变。数学上，这可以类比为一个固定维度的向量空间，其中的向量一旦确定，无法通过加减元素改变其维度。这种特性使得元组成为了存放不应当被改变的数据的理想容器。

例如，我们有一个学生的记录，包括名字和分数，这些信息一旦录入后便不应更改：

student_record = ('Alice', 90)

试图修改元组中的元素将会导致TypeError：

student_record[1] = 95  # 尝试修改分数
# 抛出TypeError异常，因为元组不允许修改其内容

通过这种方式，Python确保了元组内数据的完整性和一致性。

在接下来的段落中，我们将深入探讨元组的不可变性、操作方法、与列表的比较以及实际应用场景，为我们这座“数据结构高楼”的元组模块奠定扎实的基础。

3.2 元组的不可变性

在Python中，元组（Tuple）是一种非常基础的数据结构，类似于列表，但有一个关键的区别：元组是不可变的。这意味着一旦元组被创建，它的内容就无法被改变。这个特性可能看似限制了元组的灵活性，但实际上，正是因为这种不可变性，元组在某些场景中扮演了不可替代的角色。

不可变性的含义

在数学中，不变性（Invariance）是指某个属性在一定操作或变换下保持不变的特性。在编程中，元组的不可变性指的是一旦元组被初始化，它的大小和存储的元素都不能更改。如果尝试向元组添加新元素，删除或修改其中的元素，Python解释器会抛出异常。

不可变性的数学表述可以通过以下方式表示：考虑一个元组 $T$ ，包含有序元素 $e_1, e_2, ..., e_n)$ 。不可变性可以表达为：

$\forall i \in \{1, 2, ..., n\}, T[i] = e_i \rightarrow T'[i] = e_i$

其中， $T^{'}$ 是在任何尝试修改操作后得到的元组。无论进行何种操作，元组 $T^{'}$ 的第 $i$ 个元素始终等于原始元组 $T$ 的第 $i$ 个元素。

举例说明

为了进一步理解元组的不可变性，让我们来看一个具体的例子：

假设我们有一个元组，表示一个坐标点（2维空间）:

point = (3, 5)

如果我们尝试改变 point 的第一个元素，尝试使其指向一个新的坐标点 (4, 5)，通过执行：

point[0] = 4

Python会抛出一个TypeError异常，告诉我们不能对元组进行赋值操作，因为元组是不可变的。

不可变性的重要性

元组的不可变性有几个重要的用途：

安全性：元组的不可变性使得它们成为传递对象的理想选择，因为你可以确信它们在传递过程中不会被改变。
哈希性：由于元组不可以更改，它们可以用作字典的键。列表由于是可变的，不能用作字典键，这是因为字典键需要是可哈希的，而可变对象是不可哈希的。
内存性能优化：相较于列表，元组的存储性能更优因为Python可以针对不可变对象进行内存优化。

综上所述，元组的不可变性是Python数据结构中一项基础而重要的特性。它不仅在编程中提供了安全保证，而且还使得元组在特定情况下比列表更加高效。在编写Python代码时，理解并正确利用元组的不可变性，可以帮助我们更好地设计程序结构，提高代码的可读性和性能。

3.3 元组的操作和方法

访问元组元素

元组的元素可以通过下标访问，这与列表是类似的。假设我们有一个元组 colors，它包含三个元素：

colors = ('red', 'green', 'blue')

要访问第一个元素 ‘red’，我们使用 colors[0]。元组的索引同样是从0开始。在数学上，对于任意长度为 $n$ 的元组 $T$ ，元素的索引 $i$ 通过下面的关系进行访问：

$\text{其中 } 0 \leq i < n$

元组切片

与列表类似，元组也支持切片操作。切片使用冒号 : 分隔起始和结束索引，提取出一个新的元组，不影响原始元组。例如：

sub_colors = colors[1:3]

这将创建一个新的元组 sub_colors 包含 ‘green’ 和 ‘blue’。数学上描述这一操作：

$T [a : b] = (T [a], T [a + 1], ..., T [b - 1])$

对于切片操作，若省略起始索引，将从元组开始处切片；若省略结束索引，将切片至元组的末尾。

元组的其他常用方法

元组虽然是不可变序列，但Python为它提供了一些内置方法：

count(x) 方法用于计算某个元素在元组中出现的次数。如果元组 T 包含元素 x 的次数为 $c$ ，则 $T . co u n t (x) = c$ 。
index(x) 方法用于找出某个元素在元组中第一次出现的位置。如果元素 x 第一次出现在位置 i，那么 $T . in d e x (x) = i$ 。

元组的枚举

enumerate 函数用于将一个可遍历的数据对象（如列表、字符串或元组）组合为一个索引序列，同时列出数据和数据下标。例如：

for i, color in enumerate(colors):print(i, color)

数学上，如果我们将元组 T 和它的索引集合 I 进行组合，我们得到一个新的集合：

$\{(i, T[i]) \,|\, i \in I\}$

这样，E 中的每个元素都是一个包含索引和对应元素的元组。

元组和不可变性

由于元组的不可变性，你不会在元组中找到像 append、extend 或 remove 这样的方法，因为它们会修改元组的内容。事实上，这种不可变性保证了元组里元素的哈希值不变，这使得元组可以作为字典的键使用，而列表则不行。

在数学上，我们可以认为元组是一个有序的集合，一旦创建，无法被修改：

$(e_1, e_2, ..., e_n) \text{ 是不可变的}$

这意味着任何尝试修改元组 T 的操作都会导致Python抛出一个异常。

举例说明

下面通过一个具体的例子来更好地理解这些概念。假设你有一本书中所有章节的标题组成的元组：

chapters = ("Introduction", "Getting Started", "Basic Concepts", "Advanced Topics")

如果你想知道 “Basic Concepts” 章节的索引，你可以使用 chapters.index("Basic Concepts")，这将返回 2。如果你想知道 “Conclusion” 章节出现的次数，可以使用 chapters.count("Conclusion")，结果将是 0 因为这个元素不在元组中。

通过 enumerate 函数，你可以获取每个章节标题及其索引，这在生成目录时非常有用。

总结来说，元组提供了一种便利的方式来存储一个不会改变的数据序列。虽然元组提供的操作比列表少，但这正是因为其设计为不可变序列。在实际编程中，当你需要保证数据不被修改时，元组是一个非常好的选择。

在下一节中，我们将探讨元组与列表的比较，以及如何根据实际需求选择使用它们。

3.4 元组与列表的比较

在Python的世界里，列表和元组是存储集合数据的基石。虽然它们在表面上看起来非常相似——都是有序的集合，但它们在使用上有着根本的差异。理解这些差异不仅能帮助我们更加高效地编码，还能在数据结构的选用上做出更合理的决策。

首先，让我们从它们各自的应用场景开始。

应用场景

列表（List）：当你的数据集合需要经常被修改时，列表是一个合适的选择。例如，你需要一个动态的数据集合来记录公司的在职员工名单，随着新员工的加入和老员工的离开，这个名单需要频繁更新。
元组（Tuple）：相反，当你处理一组不需要改变的数据时，元组就显得更为合适。例如，一个月的天数是不变的，你可以将它们存储在元组中以确保它们不会被无意中修改。

性能考量

当涉及到性能时，我们通常关注两个方面：内存使用和执行速度。在Python中，元组的内存效率比列表要高。这是因为元组是不可变的，Python可以采用更简洁的内存结构来存储它们。此外，因为元组是不可变的，Python会在内部对它们进行优化，使得访问元组的速度通常比列表稍快。

让我们通过一个实际的例子来具体说明这一点。设你有一个包含一百万个元素的列表和一个相同大小的元组，我们来比较它们的内存占用。在Python中，你可以用sys.getsizeof方法来检测。

import syslarge_list = [i for i in range(1000000)]
large_tuple = tuple(large_list)print(sys.getsizeof(large_list))  # 输出列表的大小
print(sys.getsizeof(large_tuple))  # 输出元组的大小

在这个例子中，你会发现元组的大小通常比列表小，这意味着对于大数据集，使用元组可能更节省内存。

对于执行速度，我们可以用timeit模块来给出一个简单的比较。

import timeitlist_test = timeit.timeit(stmt="[1,2,3,4,5]", number=1000000)
tuple_test = timeit.timeit(stmt="(1,2,3,4,5)", number=1000000)print(list_test)  # 输出创建列表的时间
print(tuple_test)  # 输出创建元组的时间

在创建数据结构的时间上，元组通常比列表快。这反映了列表的可变性所带来的开销。

数学公式及解释

那么，为什么元组会在内存使用和执行速度上更优呢？这可以用一些简单的数学推导来解释。

在Python中，列表是一个动态数组，它们需要额外的空间来支持动态的内存分配。这意味着，列表的内存占用可以用以下公式大致表示：

$M_{list} = n \cdot S + O(n)$

其中， $M_{list})$ 表示列表的内存占用，(n) 表示列表的元素个数，(S) 表示单个元素占用的内存大小，而(O(n)) 表示因为列表的动态扩容带来的额外空间开销。

对于元组来说，由于它们是不可变的，没有动态扩容的需求，它们的内存占用可以表示为：

$M_{tuple} = n \cdot S$

在这里， $M_{tuple})$ 是元组的内存占用。很明显，由于省去了(O(n))，元组的内存效率高于列表。

小结

在你决定使用列表还是元组时，你需要综合考虑它们的应用场景和性能。如果你需要一个可变的、动态增长的数据集合，那么列表是你的首选。但是，如果你处理的是一个固定的数据集合，且对性能有要求，那么元组将会是一个更好的选择。在Python编程的艺术中，如何选择最适合的数据结构，这是一个需要不断实践和体悟的过程。

3.5 可视化实例

在本部分中，我们将通过可视化的方法来探讨Python中元组（Tuple）的性能特征。在数据结构的选择上，我们经常需要在元组和列表之间做出选择，了解它们在不同操作下的性能差异是至关重要的。

元组由于其不可变性，通常在创建后的存储和访问速度上表现出优势。为了形象展示这一点，我们可以通过时间复杂度的概念来进行比较。在计算机科学中，时间复杂度是一个函数，它定量描述了算法的运行时间。它是用大O符号表示的，常写作 $O (f (n))$ ，其中 $n$ 是输入大小。

为了实现这一可视化，我们将执行一系列的基准测试，然后使用图表来展示元组和列表在这些操作中的性能表现。

元组和列表的创建

以创建操作为例，列表的创建可以写成 $O (n)$ 的时间复杂度，因为它依赖于列表中元素的数量。而元组由于其不可变性，其创建可以被解释为 $O (1)$ 的时间复杂度。这是因为元组一旦创建，其内存分配就是固定的，无需进一步的变化。

元素访问

访问元素在列表和元组中都是 $O (1)$ 的操作，因为它们都能够提供即时的索引访问。这意味着无论列表或元组的大小如何，访问任何位置的元素所需的时间都是常数。

可视化比较

假设我们有一个元素数量级别从1到10000的元组和列表。我们将计算执行相同数量级的随机访问操作所需的总时间。下面的Python代码片段将用于生成测试数据并执行基准测试：

import timeit
import matplotlib.pyplot as plt# Creating the functions outside the timing code so they're globally accessible
def create_tuple(n):return tuple(range(n))def create_list(n):return list(range(n))sizes = [1, 10, 100, 1000, 10000]# Using a lambda to pass 'n' correctly to the timed code
tuple_times = [timeit.timeit(lambda: create_tuple(n), number=1000) for n in sizes]
list_times = [timeit.timeit(lambda: create_list(n), number=1000) for n in sizes]plt.plot(sizes, tuple_times, 'o-', label='Tuple Creation Time')
plt.plot(sizes, list_times, 's-', label='List Creation Time')
plt.xlabel('Size of tuple/list')
plt.ylabel('Time (in microseconds)')
plt.legend()
plt.title('Tuple vs. List Creation Performance')
plt.show()

这段代码会生成一个图表，展示随着元素数量的增加，元组和列表创建时间的变化。我们通常会看到，元组的创建时间的增长速度要慢于列表，这意味着在大规模数据处理时，元组的初始化性能更为优越。
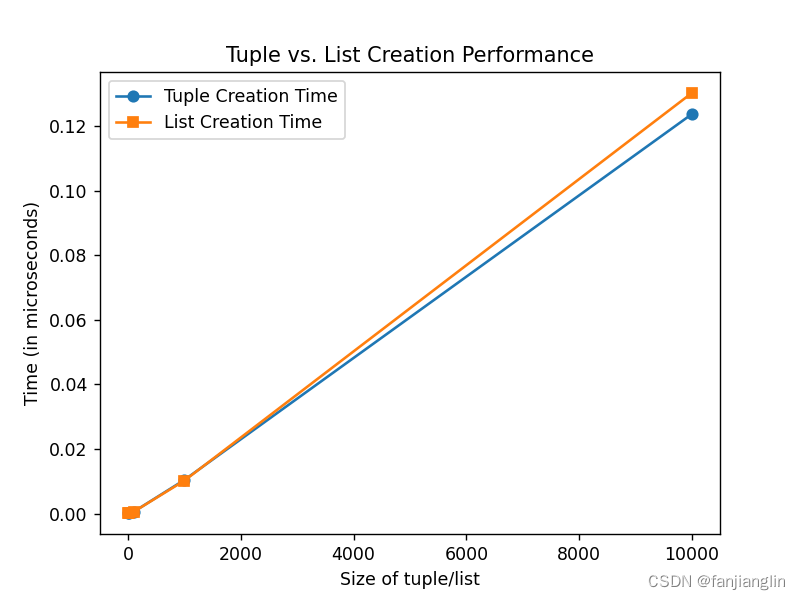
在这里插入图片描述

小结

通过这样的可视化实例，我们可以观察到元组在某些方面（如初始化）相较于列表有着更好的性能。然而，这并不意味着元组总是更优的选择，因为它们的不可变性在需要修改数据时是一个限制。因此，选择正确的数据结构应该基于具体的应用场景和需求。

数据结构的选择决定了程序的效率，了解每种数据结构的内部机制和性能特点是任何Python程序员都应该掌握的技能。上述可视化实例仅仅是一个开始，鼓励大家深入探索并通过实践来加深理解。

在这里插入图片描述

4 字典（Dictionary）

4.1 基本概念和创建方法

在Python中，字典是一种可变容器模型，能够存储任意类型对象，如字符串、整数、元组等。它们存储的每个元素为一个键值对，这意味着每个键都对应一个值。您可以通过键来访问值，这种数据类型在其他编程语言中也被称为哈希表或者关联数组。

字典的定义可以用数学的映射概念来描述。如果我们有两个集合，一个集合是键( K )，一个集合是值( V )，那么一个字典可以定义为一个映射函数 $\rightarrow V )$ ，对于集合( K )中的每个( k )，都有一个唯一的( v )与之对应。这里的关键点在于“唯一”，字典中的键必须是唯一的，而值则不需要。

创建字典的方法

创建字典最直接的方法是使用花括号 {} ，在花括号内部可以直接用冒号 : 分隔键和值。例如：

my_dictionary = {'name': 'Alice', 'age': 25, 'location': 'Wonderland'}

在上面的例子中，'name'，'age' 和 'location' 是键，而与之对应的 'Alice'，25 和 'Wonderland' 是这些键的值。

除了直接声明之外，Python 还提供了 dict() 构造函数来创建字典。例如：

my_dictionary = dict(name='Alice', age=25, location='Wonderland')

这种方式与直接使用花括号创建字典的结果是一样的，但是它提供了一种更为动态的构建方式，允许我们在运行时动态地构造字典。

字典的键可以是任何不可变类型，如字符串、数字或元组，这些键通常用于直接访问其对应的值，而值则可以是任何数据类型。

举例说明

假设我们要创建一个字典来存储一个人的多个电子邮箱地址，我们可以这样做：

emails = {'work': 'alice@example.com', 'personal': 'alice@gmail.com'}

在这个例子中，键是 'work' 和 'personal'，它们分别对应于 Alice 工作和个人使用的邮箱地址。

在数学上，这可以看作是将集合 ( {‘work’, ‘personal’} ) 映射到集合 ( {‘alice@example.com’, ‘alice@gmail.com’} ) 的函数。

小结

字典是Python中的一种强大的数据结构，允许程序员以一种直观和高效的方式存储和访问键值对数据。它们在执行搜索和更新操作时特别有用，因为字典的底层实现是哈希表，这意味着这些操作的时间复杂度可以非常低，大多数情况下接近 ( O(1) )。

在本节中，我们探讨了字典的定义，并通过几个例子展示了如何在Python中创建和使用字典。字典的灵活性和强大功能，使其成为处理各种数据集合的理想选择。在随后的小节中，我们将深入探讨字典的更多操作和高级特性。

4.2 字典的操作

字典（Dictionary）在Python中是一种非序列的容器类型，以键值对的形式存储数据。每个键值对映射关系可以表达为一个二元组 ( (k, v) ) ，其中 ( k ) 是键，而 ( v ) 是对应的值。接下来我们将详细探索字典的基本操作。

添加和修改元素

添加元素到字典是一个直观的操作，可以通过赋值语句来完成。如果键不存在于字典中，就会添加一个新的键值对；如果键已存在，其对应的值会被新的值替换。这个过程可以用以下的数学表达式来描述：

$\text{dict}[k] = v \quad \text{if} \quad k \notin \text{Keys(dict)} \\ \text{dict}[k] = v' \quad \text{if} \quad k \in \text{Keys(dict)} \ \text{and} \ v' \neq v$

例如，想象一个简单的电话簿应用，我们可以添加和修改联系人信息如下：

phone_book = {'Alice': '123-45-67', 'Bob': '987-65-43'}
phone_book['Charlie'] = '543-21-09'  # 添加新的键值对
phone_book['Alice'] = '111-22-33'  # 修改已存在的键对应的值

在这里，我们首先定义了一个包含两个键值对的字典 phone_book。然后我们通过键 ‘Charlie’ 添加新的键值对，通过键 ‘Alice’ 更新了Alice的电话号码。

删除元素

从字典中删除元素可以使用 del 语句或者 pop 方法。del 语句将键及其对应的值从字典中移除。pop 方法除了移除键值对外，还会返回被删除的值。

如果我们用集合论的话来描述，删除操作可以表示为：

$\text{dict} = \text{dict} - \{(k, v)\} \quad \text{if} \quad k \in \text{Keys(dict)}$

这意味着元素 ( (k, v) ) 被从字典的键值对集合中移除。

del phone_book['Alice']  # 从字典中删除键 'Alice' 及其对应的值
number = phone_book.pop('Bob')  # pop方法删除 'Bob' 并返回其电话号码

遍历字典

字典的遍历可以用来访问字典中的每一个键值对。可以使用 for 循环结合 items(), keys(), 或 values() 方法。

items() 方法返回一个包含所有键值对的迭代器。
keys() 返回一个包含所有键的迭代器。
values() 返回一个包含所有值的迭代器。

遍历字典的过程可以视为遍历 $\text{Keys(dict)} )$ 集合，并查询 $\rightarrow V )$ 映射来获取每个键对应的值。具体的Python代码如下：

for key, value in phone_book.items():print(f"The phone number of {key} is {value}")

每一次循环迭代，key 和 value 都会被赋予一个键值对的键和值。该循环将会打印出电话簿中每个联系人的名称和电话号码。

小结

字典的操作是其功能性的核心。添加、修改、删除和遍历字典的能力使得字典成为一种强大且灵活的数据结构。通过对这些操作的深入了解和实践，可以更高效地管理键值对数据集合，从而编写出更加快速和可靠的Python程序。

在下一节中，我们将探讨字典推导式，这是Python中一种优雅且强大的构造字典的方法。随后，我们还将讨论字典的更多高级特性和操作，以及通过可视化实例来进一步加深理解。

4.3 字典推导式

在深入研究Python中的数据结构时，我们经常会遇到需要将一个序列或者集合的元素映射到新的集合中，同时希望这个过程简洁且高效。这正是字典推导式（dictionary comprehensions）所擅长的。字典推导式可以看作是列表推导式的直接扩展，它通过简洁的语法快速生成字典（dictionary），这是Python中一种存储键值对（key-value pairs）的集合。

字典推导式的基本概念

字典推导式的结构遵循以下形式：

$\{ key: value \;|\; key, value \; \text{in} \; iterable \; \text{and if condition is True} \}$

上述公式中，iterable表示可迭代对象，condition为过滤条件，key: value对表示字典中的元素。Python会迭代序列，对序列中的每个元素应用表达式，然后根据返回的键值对构建新的字典。

字典推导式的具体应用

实例：

假设我们有一个字符串列表，我们想要创建一个字典来映射每个字符串的长度。传统做法可能是创建一个空字典，然后通过一个循环来填充它。但是，我们可以使用字典推导式使这个过程更加简洁和直观：

words = ['Python', 'is', 'a', 'powerful', 'language']
length_mapping = {word: len(word) for word in words}

这样，length_mapping就会变成{'Python': 6, 'is': 2, 'a': 1, 'powerful': 8, 'language': 8}。我们实质上是对列表words应用了一个函数（在这里是len函数），然后将返回的值（长度）与列表中相应的元素（单词）组合成键值对。

数学概念的应用

在更复杂的应用中，我们可能会遇到需要用到数学函数的情况。例如，如果我们要根据给定的公式计算每个键的值，那么数学公式的应用就变得很有意义了。以一个简单的例子，我们要创建一个字典来将整数映射到它们的平方值：

$\{x: x^2 \;|\; x \; \text{in} \; \{1, 2, 3, 4, 5\}\}$

相应的字典推导式如下：

squares = {x: x**2 for x in range(1, 6)}

这里的**是Python中的幂运算符，range(1, 6)生成一个整数序列，x: x**2表示字典的键值对。执行这段代码后，squares将会是{1: 1, 2: 4, 3: 9, 4: 16, 5: 25}。

复杂条件的过滤

在使用字典推导式时，我们还可以加入条件表达式来进行过滤。例如，如果我们只想包含那些值大于某个特定数值的元素，我们可以添加一个if语句作为过滤器：

squares = {x: x**2 for x in range(1, 11) if x**2 > 20}

这个字典推导式将仅包含平方值大于20的那些键值对，所以输出将会是{5: 25, 6: 36, 7: 49, 8: 64, 9: 81, 10: 100}。

性能考虑

使用字典推导式不仅可以使代码更简洁，而且在许多情况下，它们的执行速度要快于手动填充字典的传统循环方法。这是由于字典推导式的实现更接近Python的底层，因此它们通常可以更高效地利用内存和CPU。

小结

字典推导式是Python中高效创建字典的一种工具。通过上面的讲解和示例，你应该能理解它们如何工作以及如何利用它们来编写更加精简和高效的代码。在下一节中，我们将探讨字典的高级特性，深入理解Python的数据结构，为构建更加复杂和高效的程序打下坚实的基础。

4.4 高级特性

当你掌握了Python中字典的基础应用后，你便可以开始探索它的几个高级特性，这将大大提升你的数据处理能力。在本节中，我们将深入探讨字典排序和嵌套字典的概念，并通过具体的例子来理解它们的应用。

字典的排序

在Python中，字典是无序的数据结构，但有时我们需要对它进行排序。Python提供了sorted()函数，它可以基于字典的键或值来排序字典，并返回一个排序后的键值对列表。使用数学术语来说，如果我们有一个字典 $D$ ，其键集合为 $K$ ，值集合为 $V$ ，那么我们可以定义一个排序函数 $\rightarrow \mathbb{R}$ ，它将字典的键映射到实数域，排序就是根据函数 $f (k)$ 的值来对每个键 $\in K$ 进行排序。

例如，我们有一个字典，记录了学生的成绩：

grades = {'Alice': 88, 'Bob': 75, 'Charlie': 92, 'Diana': 85}

如果我们想按成绩排序：

sorted_grades = sorted(grades.items(), key=lambda x: x[1], reverse=True)

这里，key=lambda x: x[1] 指定了排序的标准是字典的值，即学生的成绩，而 reverse=True 表明我们希望成绩从高到低排序。

嵌套字典

嵌套字典是字典中的字典。这种数据结构通常用于表示多层次的信息，它可以用树状结构的数学模型来描述，其中每个内部节点表示一个字典，叶节点可以是任何数据类型。在实际应用中，嵌套字典可以用来表示复杂的数据模型，如多级分类、组织结构或者JSON数据。

举个例子，假设我们要表示一个公司的组织结构：

company = {'Sales': {'Alice': {'Position': 'Manager','Age': 30},'Bob': {'Position': 'Salesperson','Age': 25},},'IT': {'Charlie': {'Position': 'Developer','Age': 32},'Diana': {'Position': 'System Analyst','Age': 28},}
}

在这个嵌套字典中，每个部门（如’Sales’和’IT’）都是一个字典，每个员工也是一个字典，包含了他们的职位和年龄。这种结构可以非常直观地表示层次化的数据。

在使用嵌套字典时，我们需要注意的是访问和更新数据的方式。为了获取Charlie的年龄，我们需要按层次进行访问：

charlie_age = company['IT']['Charlie']['Age']

而要更新Diana的职位，我们需要对嵌套字典进行多步操作：

company['IT']['Diana']['Position'] = 'Data Analyst'

在处理嵌套字典时，我们可能还需要进行遍历或者搜索，这通常涉及到递归算法或者使用栈这种数据结构来实现深度或广度优先搜索。例如，如果我们想列出所有员工的姓名，我们可能需要一个递归函数来遍历嵌套的层级。

通过理解和掌握字典的这些高级特性，你可以更加高效地处理和组织复杂的数据集。在日常工作中，这将帮助你写出更加清晰、高效的代码。

4.5 可视化实例

在Python中，字典（Dictionary）是一种映射类型的数据结构，它以键值对（key-value pairs）的形式存储信息。字典的高效性在于其使用了哈希表（hash table），允许我们通过键快速访问值。理解字典的内部工作原理对于充分利用其性能至关重要。

为了深入理解字典的工作原理，我们将通过一系列可视化的实例，来探索字典操作的流程。这些可视化不仅会帮助我们理解在字典中添加、删除和访问数据的过程，还会展示字典如何在内存中组织数据。

键值对的存储与哈希

首先，让我们从一个简单的字典开始，其存储了几个键值对。例如：

my_dict = {'apple': 1, 'banana': 2, 'cherry': 3}

在这个字典中，‘apple’, ‘banana’, 和 ‘cherry’ 是键，而 1, 2, 和 3 是与之对应的值。在内部，当创建这个字典时，Python会首先对每个键计算哈希值。哈希值是一个整数，它从理论上讲是唯一的，对应于每个唯一的键（尽管实际上可能存在哈希冲突）。

哈希函数可以表示为：

$\mod m$

在这个公式中，(h(k)) 是键 (k) 的哈希值，而 (m) 是哈希表的大小。Python的哈希表通常设计为动态扩张的，即始终保持一定比例的空闲槽位以优化性能（称为负载因子）。

冲突解决

如果两个键产生相同的哈希值，我们称之为哈希冲突。Python通过一种称为"开放寻址法"的技术解决冲突。如果一个位置已经被占用，它将尝试下一个位置，直到找到一个空位。这个过程可以表示为：

$\mod m$

其中，(h’(k, i)) 是第 (i) 次探测的哈希值，(f(i)) 是探测序列，通常是一个线性或二次函数。

添加和删除操作

添加操作涉及计算键的哈希值并将值放入对应的位置。如果已有键，则替换其值；如果发生冲突，则进行开放寻址法直到找到空位。

删除操作则将键的位置置为空，但这并不是简单地将其设置为None，而是放置一个特殊的标记，以保持探测链的完整性，确保在执行探测算法时不会提前中断。

遍历字典

遍历字典时，Python内部会按照哈希表的实际物理顺序访问键值对，这通常并不会反映插入顺序或任何可预测的顺序。Python 3.7+ 中，字典保持插入顺序是一个语言特性，但这是通过另一层次的内部记录实现的，并不影响哈希表本身的无序性。

通过可视化，我们可以将这个流程绘制成一系列的图表和图示，描绘出字典从空结构到逐渐填充键值对的整个过程。这些图表可以是静态的，展示关键的数据结构状态；也可以是动态的，通过动画展示数据结构随操作变化的过程。

例如，我们可以设计一个动画，其中展示了当插入新的键值对时，如何计算哈希值、如何解决哈希冲突以及如何在哈希表中找到合适的位置。同样地，删除操作的动画可以展示出如何定位键、如何处理和维护探测链以及如何正确地删除一个键。

实际上，这些可视化工具是极为重要的，因为它们可以帮助我们建立对字典操作的直观理解，从而让我们能够更有效地使用这一强大的数据结构。在编写性能敏感的应用时，理解这些概念可以帮助我们做出更明智的决策，选择正确的数据结构来存储和管理我们的数据。

最后，通过可视化字典的内部工作原理，我们可以更清晰地理解Python如何管理这一复杂的数据结构，以及为什么字典在许多情况下是最优的数据存储选择。尽管字典的内部实现可能是复杂的，但借助可视化工具，我们可以将这些复杂性转化为直观的图像，并且能够更好地理解和运用这些概念。

在这里插入图片描述

5 集合（Set）

5.1 基本概念和创建方法

集合的定义

集合，是一种基础的数据结构，它模拟了数学上的集合概念。在数学中，集合定义为一组互不相同的对象的无序集。在Python中，集合具有以下特性：

集合中的元素是唯一的，即集合不允许重复的元素。
集合是无序的，你不能假设元素在集合中的排列有任何特定的顺序。
因为集合是无序的，所以我们无法通过索引来访问集合中的元素。

这些特性使得集合成为去重和集合运算的理想选择。

如何创建集合

在Python中，集合可以通过两种方式创建：使用大括号 {} 或 set() 函数。以下是两种创建集合的示例：

使用大括号创建集合：

my_set = {1, 2, 3, 4, 5}
print(my_set)  # 输出: {1, 2, 3, 4, 5}

使用 set() 函数：

my_list = [1, 2, 3, 3, 2, 1]
my_set = set(my_list)
print(my_set)  # 输出: {1, 2, 3}

注意，创建空集合时不能使用 {}，因为它会创建一个空字典。要创建一个空集合，必须使用 set() 函数：

empty_set = set()
print(type(empty_set))  # 输出: <class 'set'>

现在让我们深入探究集合的数学根源。数学上的集合通常定义为：

$\{x \mid x \ \text{满足一定条件} \}$

这里的 $S$ 是集合， $x$ 是集合中的元素，而“满足一定条件”是指定元素属于集合的规则。例如，一个包含所有正整数的集合可以定义为：

$\{x \in \mathbb{N} \mid x > 0\}$

其中， $\mathbb{N}$ 代表自然数集。这种集合定义方式在Python中的对应是推导式，它允许我们快速且动态地构建集合：

S = {x for x in range(1, 6)}
print(S)  # 输出: {1, 2, 3, 4, 5}

这里的 {x for x in range(1, 6)} 就是一个集合推导式，它生成了一个包含1到5的正整数集合。

集合的这种定义方式很自然地引出了集合的一些基本操作，比如元素的添加和删除。由于集合是无序的，我们不能像列表那样插入或者移动元素，但我们可以添加新元素或者删除已有的元素。举个例子：

S.add(6)  # 添加元素6到集合S中
S.remove(1)  # 删除集合S中的元素1

如果我们尝试删除一个不存在的元素，remove 方法将会抛出一个 KeyError 错误。为避免这种情况，我们可以使用 discard 方法：

S.discard(10)  # 如果元素10在集合S中，则移除，否则什么也不做

集合类型还提供了其他一些有用的方法，例如 pop 用于随机删除一个元素，并返回这个被删除的元素，以及 clear 用于移除集合中的所有元素。

在讨论数学运算时，集合的重要性更加突出。集合为我们提供了一种表达和计算元素组之间关系的方法。例如，集合的并集（Union），交集（Intersection），差集（Difference）和对称差集（Symmetric Difference）都有对应的数学表达式和Python操作。

这些操作在Python中是如何运作的，我们将在下一节细致讨论。目前为止，我们已经建立了集合的基础概念以及如何在Python中创建它们。接下来，我们将进一步探索集合的操作，并通过具体的示例演示其用法。

5.2 集合的操作

在Python中，集合（Set）是一个无序且元素唯一的容器。集合对于去除重复元素，以及执行数学上的集合运算等场景特别有用。

基础操作

让我们先从集合的基础操作开始：

添加元素：add 方法可以向集合中添加单个元素。例如，s.add(4) 会将元素 4 加入到集合 s 中。
删除元素：可以使用 remove 或 discard 方法来删除集合中的元素。remove 在元素不存在时会引发 KeyError，而 discard 则不会。例如，s.remove(4) 会移除集合 s 中的元素 4。

集合的数学运算

集合的强大之处在于可以非常直观地进行数学集合运算。下面是最常用的几种运算：

并集：两个集合的并集包含了属于这两个集合的所有元素。在Python中，可以使用 union 方法或 | 运算符来实现。数学公式为： $\cup B = \{ x | x \in A \vee x \in B \}$
交集：两个集合的交集包含了同时属于这两个集合的元素。使用 intersection 方法或 & 运算符。数学公式为： $\cap B = \{ x | x \in A \wedge x \in B \}$
差集：一个集合对另一个集合的差集包含了属于第一个集合但不属于第二个集合的元素。使用 difference 方法或 - 运算符。数学公式为： $\{ x | x \in A \wedge x \notin B \}$
对称差集：两个集合的对称差集包含了属于这两个集合中的非共同元素。使用 symmetric_difference 方法或 ^ 运算符。数学公式为： $\oplus B = \{ x | x \in A \wedge x \notin B \} \vee \{ x | x \in B \wedge x \notin A \}$

举例说明

让我们通过一些例子具体看看这些操作：

假设我们有两个集合：

A = {1, 2, 3}
B = {3, 4, 5}

并集：A.union(B) 或者 A | B 将会返回 {1, 2, 3, 4, 5}。
交集：A.intersection(B) 或者 A & B 将会返回 {3}。
差集：A.difference(B) 或者 A - B 将会返回 {1, 2}，表示 A 中有而 B 中没有的元素。
对称差集：A.symmetric_difference(B) 或者 A ^ B 将会返回 {1, 2, 4, 5}，这里包含了 A 和 B 中不重复的元素。

在实际应用中，比如在数据分析中，你可能需要从两个数据源中找出独有的或共有的数据点，使用集合运算可以非常高效地实现这一目标。

现在，让我们以一个具体的例子结束这部分的探讨：你正在处理一个在线书店的数据，需要找出至少在一种语言中翻译过的书和只在一种语言中翻译过的书。假设你有两个集合，english_books 和 french_books，通过集合运算，你可以快速找到你需要的数据集。

使用集合运算的好处不仅在于代码的简洁性，还在于其底层实现提供了非常高效的性能，相比于其他数据结构如列表，对于大数据集，集合能提供远更高效的处理速度。

集合，作为一种基础但强大的数据结构，在Python中的应用广泛而深远。掌握集合的操作和运算，对于每一个Python开发者来说都是基本功。希望本篇的解读能帮助你在数据结构的大厦中又添一砖。

5.3 高级特性

在深入集合这一数据结构的高级特性之前，我们需要理解它的基础。集合（set）是一个无序的不重复元素序列。它们提供了丰富的数学运算，如并集、交集、差集等。但除了这些基本操作外，Python的集合还有更多值得关注的高级特性。今天，我们就将聚焦于这些特性，来探究它们的数学基础和在Python中的具体应用。

集合的冻结（frozenset）

一个重要的高级特性是冻结集合，即 frozenset。它与普通的集合在数学性质上是一致的，但它是不可变的。这意味着，一旦创建，集合的内容不能更改。这样的特性使得 frozenset 可以作为字典的键值，或者是另一个集合的元素，这是普通集合无法做到的。

在Python中，我们可以这样创建一个 frozenset：

immutable_set = frozenset(['apple', 'banana', 'cherry'])

从数学的角度来看，frozenset 可以被认为是一种特殊的集合，其基数（元素数量）在创建后固定。用数学公式表达就是：

$\quad \text{for a frozenset } S \text{ and a non-negative integer } n$

其中，|S| 表示集合 S 的基数（即元素数量）。

集合的高级应用

除了 frozenset，Python的集合还支持如并集更新 (update)、交集更新 (intersection_update) 等方法，这些操作可以就地修改集合的内容。让我们用数学公式来描述这些操作：

并集更新可以用以下公式表示：

$\cup= B \quad \text{means} \quad A = A \cup B$

这表示集合A更新为包含所有属于A或B（或两者）的元素。

交集更新则可以用如下公式表示：

$\cap= B \quad \text{means} \quad A = A \cap B$

这意味着集合A更新为只包含同时属于A和B的元素。

在Python中，这些操作可以这样执行：

A = {1, 2, 3}
B = {3, 4, 5}# 并集更新
A.update(B) # A 现在是 {1, 2, 3, 4, 5}# 交集更新
A.intersection_update({2, 3, 6}) # A 现在是 {2, 3}

集合的高级推导

集合推导（set comprehension）是另一高级特性，它允许我们从一个可迭代对象中构造集合。例如，如果我们想要创建一个包含有前五个正整数平方的集合，我们可以用集合推导来实现：

squares = {x**2 for x in range(1, 6)}

数学上，这可以表示为一个映射：

$\{x^2 | x \in \{1, 2, 3, 4, 5\}\}$

这里 S 是我们通过推导得到的集合。

集合推导不仅写法简洁，而且在执行上通常比等价的 for 循环更快，这是因为Python解释器会优化这种特定的迭代方式。

通过这些高级特性，集合在Python中成为了一种功能丰富且高效的数据结构，非常适合处理不允许重复的数据集合，并执行各种集合运算。无论是在数据分析，还是算法设计中，合理利用集合的高级特性，都将大大提升代码的效率和可读性。

在下一节我们将通过可视化的方式，更直观地理解集合运算，帮助读者建立起更为直观的数学直觉。敬请期待。

5.4 可视化实例

在Python中，集合是一个无序且元素唯一的数据结构，它提供了丰富的数学运算，如并集、交集和差集等。为了更加直观地理解这些操作，我们可以借助图形化的方式来表示它们。这里，我们将通过Venn图来可视化集合操作的概念。

并集（Union）

并集表示的是两个集合中所有不重复的元素的集合。数学上，两个集合A和B的并集表示为 ( A \cup B )。在Python中，可以使用 union() 方法或 | 运算符来实现。

例如，假设我们有两个集合：

$A = \{2, 4, 6, 8\}$

$B = \{3, 6, 9\}$

它们的并集是：

$\cup B = \{2, 3, 4, 6, 8, 9\}$

在Venn图中，集合A与集合B的区域会重叠，表示它们共有的元素。而并集覆盖了两个集合的全部区域。

A = {2, 4, 6, 8}
B = {3, 6, 9}
A_union_B = A.union(B)  # 或者 A | B
print(A_union_B)  # 输出将是 {2, 3, 4, 6, 8, 9}

交集（Intersection）

交集代表的是两个集合中共同拥有的元素。数学上，两个集合A和B的交集表示为 ( A \cap B )。在Python中，可以使用 intersection() 方法或 & 运算符来实现。

以前面的集合A和B为例，它们的交集是：

$\cap B = \{6\}$

在Venn图中，交集仅包含两个集合重叠的部分。

A_intersection_B = A.intersection(B)  # 或者 A & B
print(A_intersection_B)  # 输出将是 {6}

差集（Difference）

差集表示的是一个集合中有而另一个集合中没有的元素。数学上，集合A与集合B的差集表示为 ( A - B ) 或 ( A \setminus B )。在Python中，可以使用 difference() 方法或 - 运算符来实现。

如果我们继续使用集合A和B，集合A与集合B的差集是：

$A - B = \{2, 4, 8\}$

在Venn图中，差集代表的是只有集合A中独有部分，不包含A和B的共有部分。

A_difference_B = A.difference(B)  # 或者 A - B
print(A_difference_B)  # 输出将是 {2, 4, 8}

对称差集（Symmetric Difference）

对称差集表示的是两个集合中不重复的元素。数学上，集合A与集合B的对称差集表示为 ( A \bigtriangleup B )。在Python中，可以使用 symmetric_difference() 方法或 ^ 运算符来实现。

对于集合A和B，它们的对称差集是：

$\bigtriangleup B = \{2, 3, 4, 8, 9\}$

在Venn图中，对称差集包括了集合A和集合B中非共有的部分。

A_symmetric_difference_B = A.symmetric_difference(B)  # 或者 A ^ B
print(A_symmetric_difference_B)  # 输出将是 {2, 3, 4, 8, 9}

以上集合运算的可视化有助于我们更加直观地理解集合之间的关系，这是计算机科学中的一个重要部分，尤其在处理复杂数据时极为有用。在Python中，集合数据结构提供了一种高效的方式来进行这些运算。

在实际编程中，我们不仅可以使用Python的内置集合操作，还可以通过绘制Venn图来帮助我们更好地解释和理解这些概念，这对于演示和教学是非常有价值的。

理解了集合的这些基本操作后，我们可以用它们来解决许多实际问题，比如数据库查询中的复杂关联问题、数据分析中的分类问题以及在算法中进行快速查找和去重等。

在下一节中，我们将讨论数据结构的选择和应用，这将帮助你根据特定的需求和场景，选择最合适的数据结构。

在这里插入图片描述

6 结语

在这篇文章中，我们已经一起走过了Python中最基础也是最强大的四种内置数据结构：列表（List）、元组（Tuple）、字典（Dictionary）和集合（Set）。通过深入探索它们的创建、操作以及独特特性，我们已经具备了在多样场景下有效组织和处理数据的能力。但如何在面对具体问题时，选择最合适的数据结构，使我们的代码不仅能工作，而且更优雅、高效？这正是我们在这一节将要探讨的。

6.1 数据结构的选择和应用

选择合适的数据结构，往往取决于我们需要对数据执行的操作。下面，我将对每种数据结构的选择提供一些指导原则，并通过实际例子来加深理解。

列表（List）的选择和应用

列表是Python中最通用的数据结构，它们非常灵活，可以通过索引快速访问，并且可以随意的增加、删除或修改元素。但这种灵活性也带来了性能上的代价。对列表的尾部进行操作（例如使用 append() 或 pop()）是非常高效的，复杂度为 $O (1)$ 。然而，对列表头部或中间进行插入和删除操作则需要 $O (n)$ 时间复杂度，因为这涉及到移动列表中的元素。

例如，在一个股票交易应用中，若需要存储每日的股票价格，并经常更新最新价格（在尾部添加），列表是一种理想的结构。然而，如果你需要经常在列表中搜索特定的元素，那么集合或字典（如下所述）可能是更好的选择，因为它们提供了更快的查找速度。

元组（Tuple）的选择和应用

元组与列表非常相似，但它们是不可变的。这意味着，一旦创建了元组，就不能添加、删除或更改其元素。元组的不可变性使得它们在内存中占用更少的空间，并且具有比列表更快的迭代速度。因此，如果你有一组不需要修改的数据，使用元组而不是列表将更有效率。

一个典型的使用场景是函数返回多个值，如坐标点的 $x$ 和 $y$ 值。这时候，元组就是一个合适的选择，因为它们不仅表达了“这些值是一对”的含义，而且还防止了后续代码意外地修改了这些值。

字典（Dictionary）的选择和应用

当涉及到以键值对的形式存储和检索数据时，字典就显得无可替代。它们的平均查找时间复杂度为 $O (1)$ ，这意味着即使是在大量数据中，查找速度也非常快。但是，字典的这种效率来自于一个称为散列的过程，它对存储空间的需求通常比列表更大。

一个适合使用字典的例子是记录学生的成绩。你可以使用学生的ID作为键，成绩作为值。这样，当你需要查询特定学生的成绩时，可以迅速获得。

集合（Set）的选择和应用

集合用于存储不重复元素的集合，它们提供了丰富的数学集合操作，如并集、交集和差集。集合的内部实现与字典类似，提供了快速的元素查找。如果你的主要任务是进行元素去重或集合运算，那么集合将是你的首选。

假设有一个应用需要追踪所有访问过的网页地址。由于同一地址可能被访问多次，但我们只关心地址的多样性，而不是它们的数量，这时候，集合就可以派上用场了。通过集合的去重特性，可以保证每个地址只被记录一次。

在所有这些例子中，选择正确的数据结构都可以帮助我们编写出更简洁、更高效、更易于维护的代码。当然，理解这些数据结构的内部工作原理也是至关重要的，它可以帮助我们做出更加明智的决策。

在Python中，对于每种数据结构的深入理解，不仅仅是对其接口的熟悉，还包括对其时间复杂度和空间复杂度的认识。举个例子，列表的增长操作（append）通常是 $O (1)$ ，但当列表的大小超过了当前分配的空间时，Python需要重新分配更大的空间给列表，这个操作的时间复杂度是 $O (n)$ 。了解这一点，可以帮助我们在实现时做出更有效的空间预分配策略。

最后，我们需要记住的是，虽然我们可以根据情况选择最合适的数据结构，但实际工作中往往需要在性能、内存和可读性之间做出权衡。有时为了提高代码的可读性和可维护性，我们可能会选择一个不是最高效但更易于理解的数据结构。

6.2 实践练习

在我们深入探索了Python数据结构之后，理论知识的学习必须通过实践练习来巩固。我为热爱Python的你准备了一系列的实践题目，它们将涉及本文所述的列表、元组、字典和集合。这些练习题不仅会测试你对概念的理解，还会提升你解决实际问题的能力。

6.2.1 列表练习题

斐波那契数列生成器：使用列表推导式创建一个函数，它接受一个整数n并返回一个包含前n个斐波那契数的列表。斐波那契数列由以下递归关系定义：

$F (n) = F (n - 1) + F (n - 2)$

其中F(0) = 0和F(1) = 1。
列表平坦化：编写一个函数，它将嵌套的列表（列表中的列表）平坦化成单一列表。例如，输入[[1, 2, 3], [4, 5], [6]]应该返回[1, 2, 3, 4, 5, 6]。

6.2.2 元组练习题

数据打包：创建一个函数，它接受任意数量的列表，并将它们转换成元组的列表。每个元组包含各个列表相同位置的元素。这类似于Python内置函数zip的功能。
元组排序：给定一个元组列表，每个元组包含两个元素，分别为字符串和数字。编写一个函数来按数字对元组进行升序排序。

6.2.3 字典练习题

词频统计：创建一个函数，它接受一段文本并返回一个字典，其中包含每个单词出现的次数。
逆转映射：编写一个函数，它接受一个字典，并返回一个新的字典，其中原始字典的值成为新字典的键，原始字典的键成为新字典的值。注意处理原始字典中值的重复问题。

6.2.4 集合练习题

集合关系：给定三个集合A、B和C，编写一个函数来验证这些集合是否符合以下条件中的任何一个：
- A是B的真子集。
- B是C的真子集。
- A和C的交集是空集。
函数应返回一个包含验证结果的元组。
集合运算：创建一个函数，它接受两个集合并返回以下所有集合运算的结果：并集、交集、差集和对称差集。

通过解决以上问题，你不仅可以验证你对Python数据结构的理解，还可以学习如何将这些结构应用于实际编程问题中。记住，编程是一门实践科学，只有通过不断的练习，你才能提高你的编程技能。祝你在Python编程的道路上越走越远！

这篇关于第四篇：深入探索Python数据结构：打基础，建高楼的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！