红黑树插入/删除的几种情况，图论，拓扑学杂烩

本文主要是介绍红黑树插入/删除的几种情况，图论，拓扑学杂烩，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

红黑树的操作复杂度为 $O(log^n_2)$ ,也就是说，如果有10亿的序列查找也不会超过30次，效率非常高。

红黑树的结构具有分形结构，局部树和整个树遵守相同的红，黑设置规则。

0.父节点为黑色，不需要任何操作

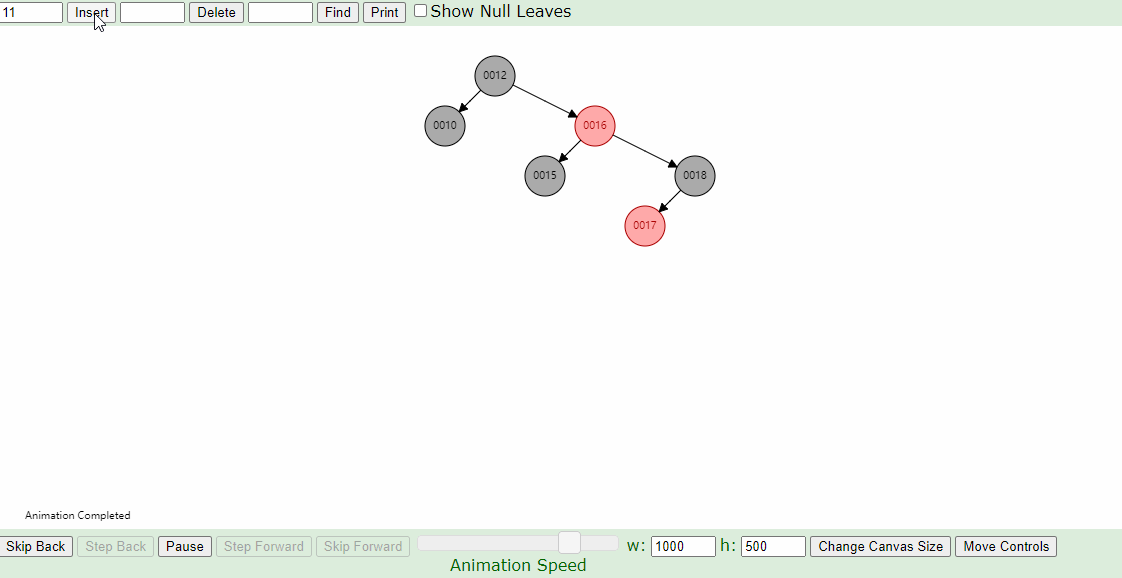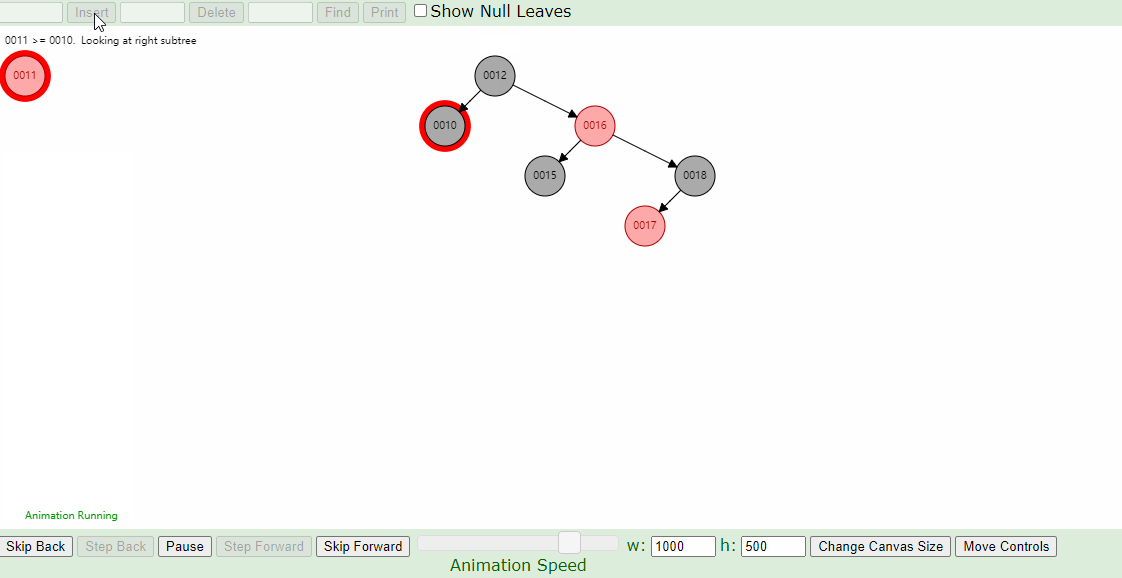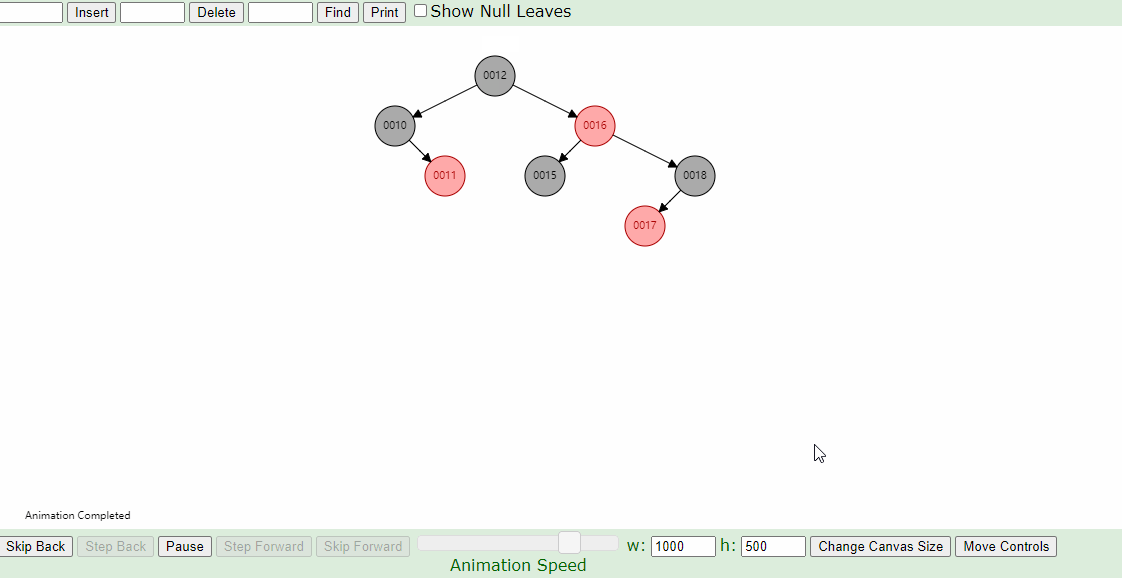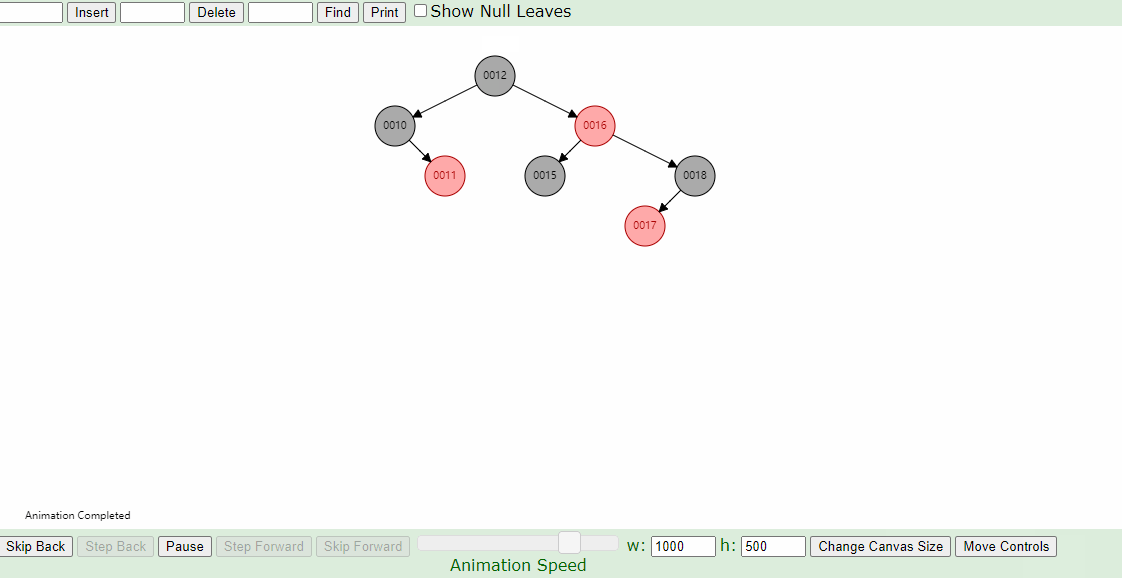
1.新插入的节点父节点为红色，叔叔节点也为红色操作步骤

首先将叔叔和父节点改为黑色，爷爷节点改为红色，进入下一步
将爷爷节点作为当前插入节点看待，一直进行上面的操作，直到当前结点为根结点，然后将根结点变成黑色
此时变为，新插入节点的父节点为红色，但是叔叔节点变为了黑色。插入结点是左结点，父亲结点是右结点.
此时进行右旋，右旋后插入节点变为9号节点
此时，9号节点作为插入节点，符合父节点为红色，叔叔节点为黑色，并且父亲结点为爷爷结点的右孩子，新插入结点为父亲结点的右孩子的右右情况。
接着我们将父节点和爷爷节点的颜色互换。
在进行一次左旋
结束！

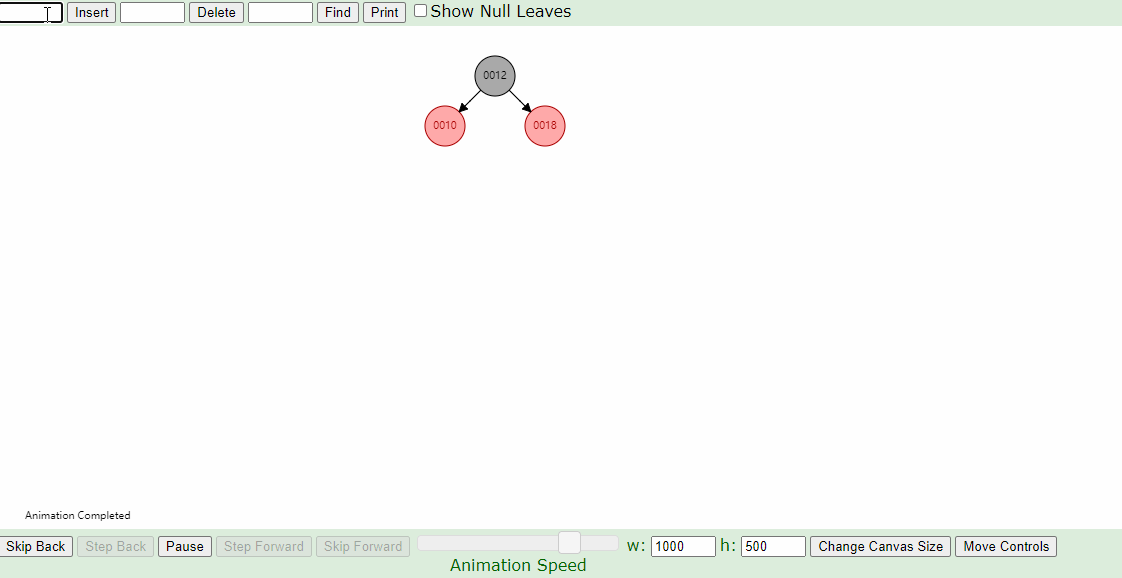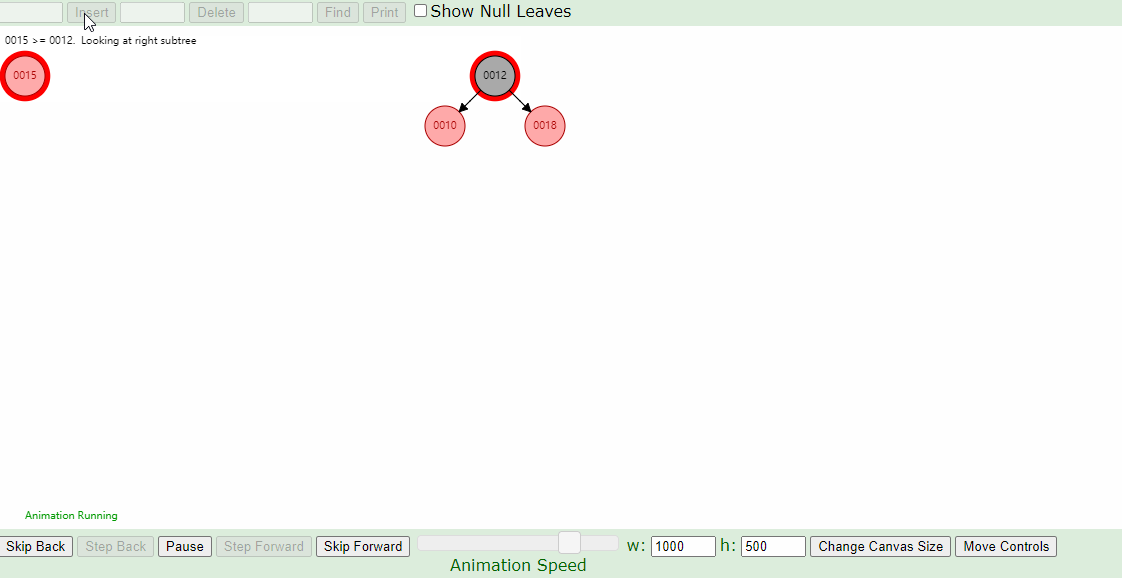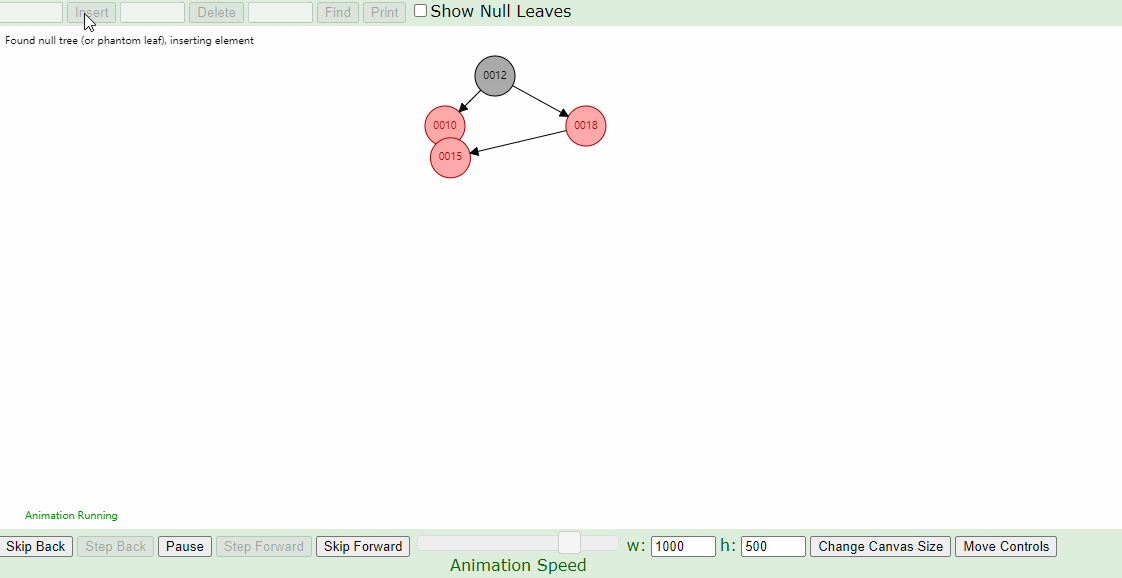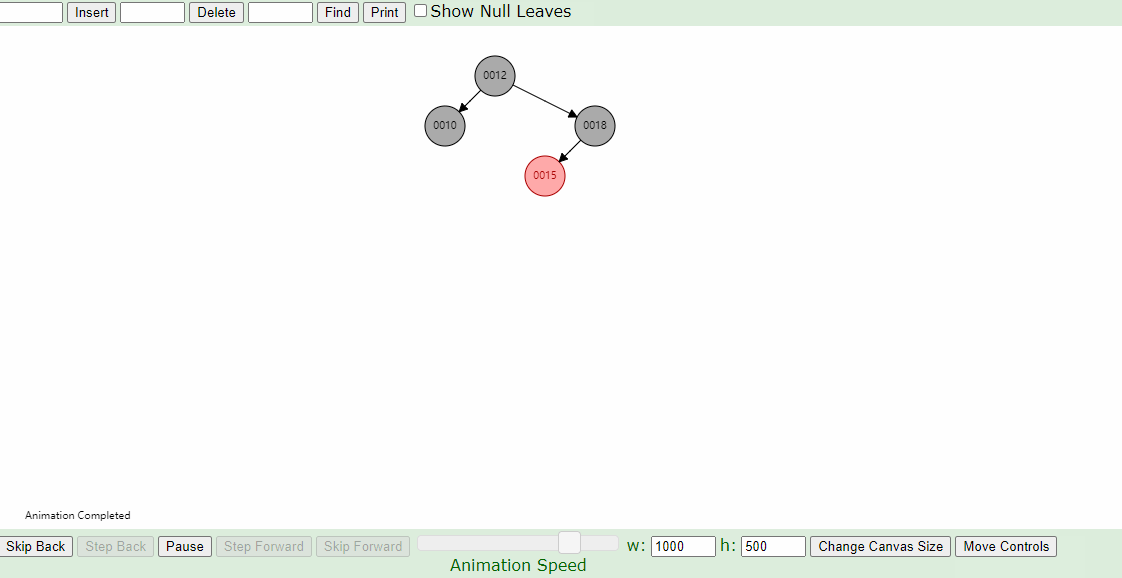
2.新插入的节点的父节点为红色，叔叔节点为黑色的情况:

下图插入的节点的父节点为红色(#2)，叔叔节点为黑色（1号的左叶子节点也算叔叔节点)，这个时候，父亲结点为爷爷结点的右孩子，新插入结点为父亲结点的右孩子（右右情况），只要将父节点和爷爷节点颜色互换，并针对爷爷节点做一次左旋，如下图即可。

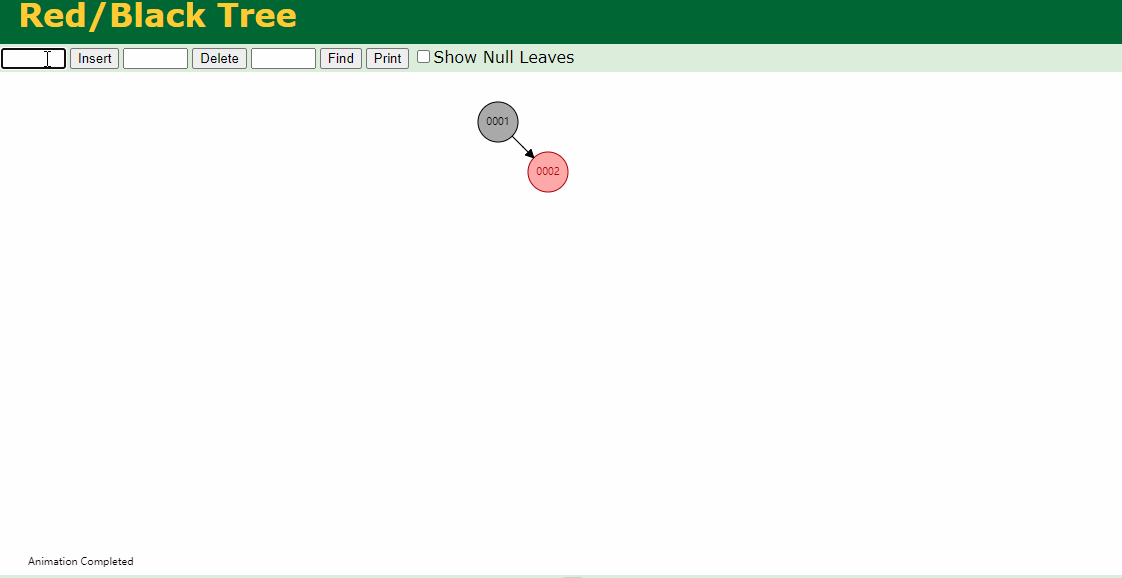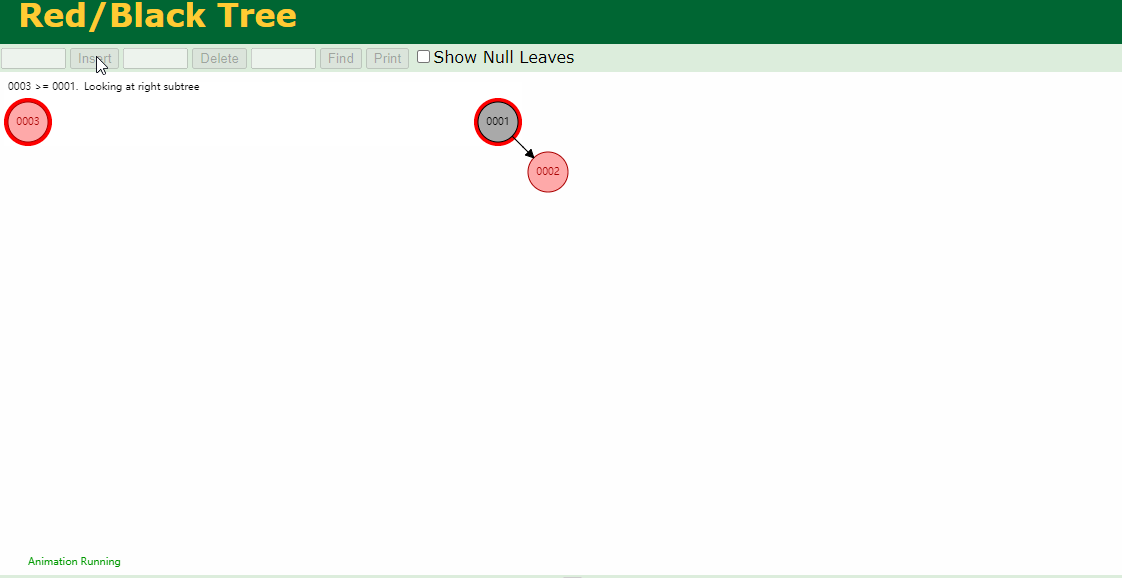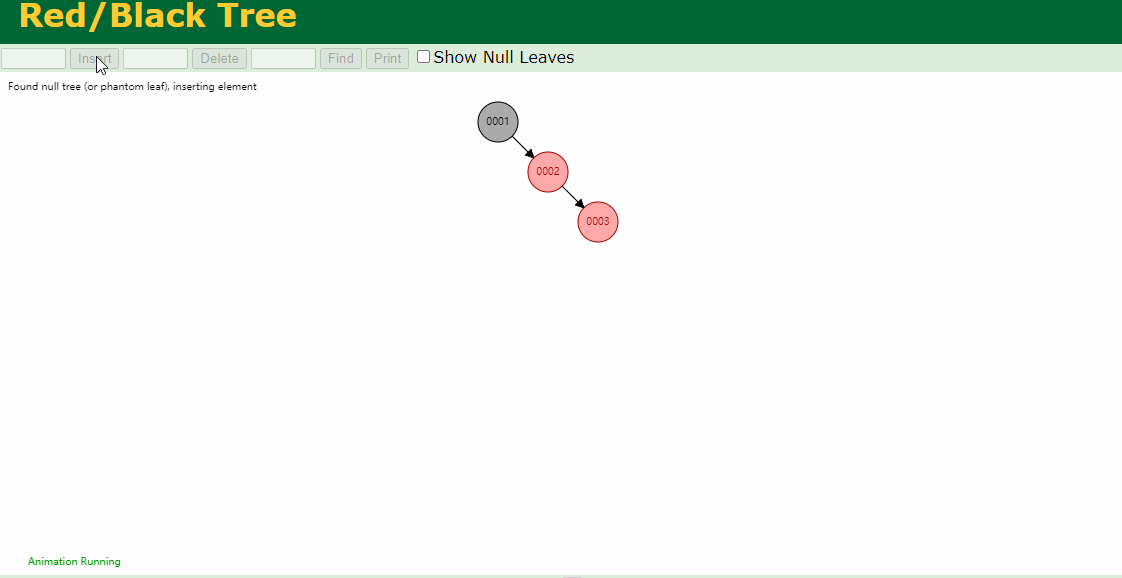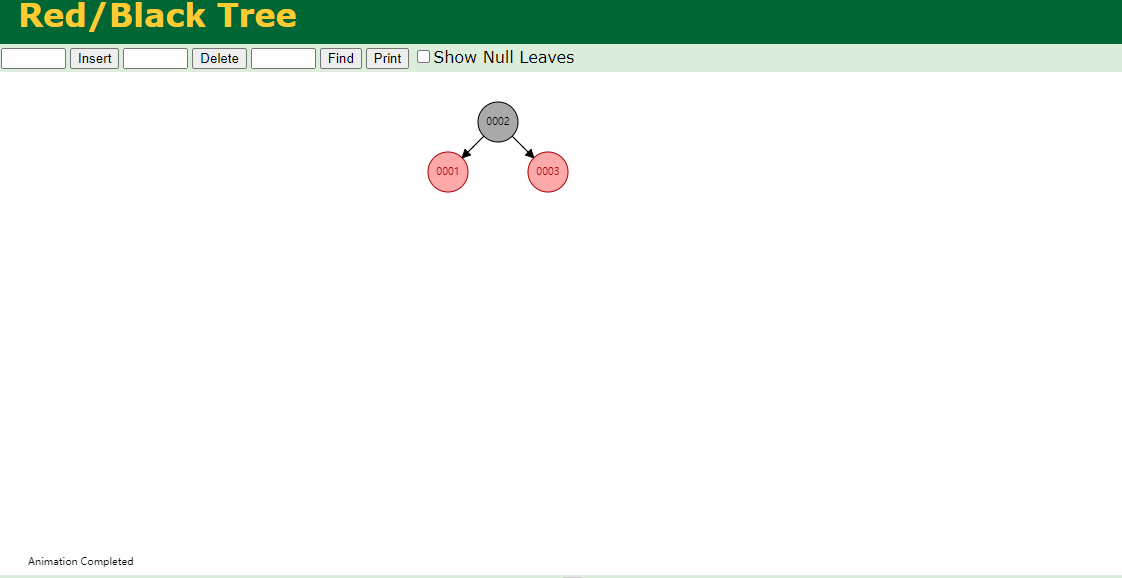
下图插入的节点的父节点为红色(#7)，叔叔节点为黑色（#8的右叶子节点也算叔叔节点)，这个时候，父亲结点为爷爷结点的左孩子，新插入结点为父亲结点的左孩子（左左情况），只要将父节点和爷爷节点颜色互换，并针对爷爷节点做一次右旋，如下图即可。

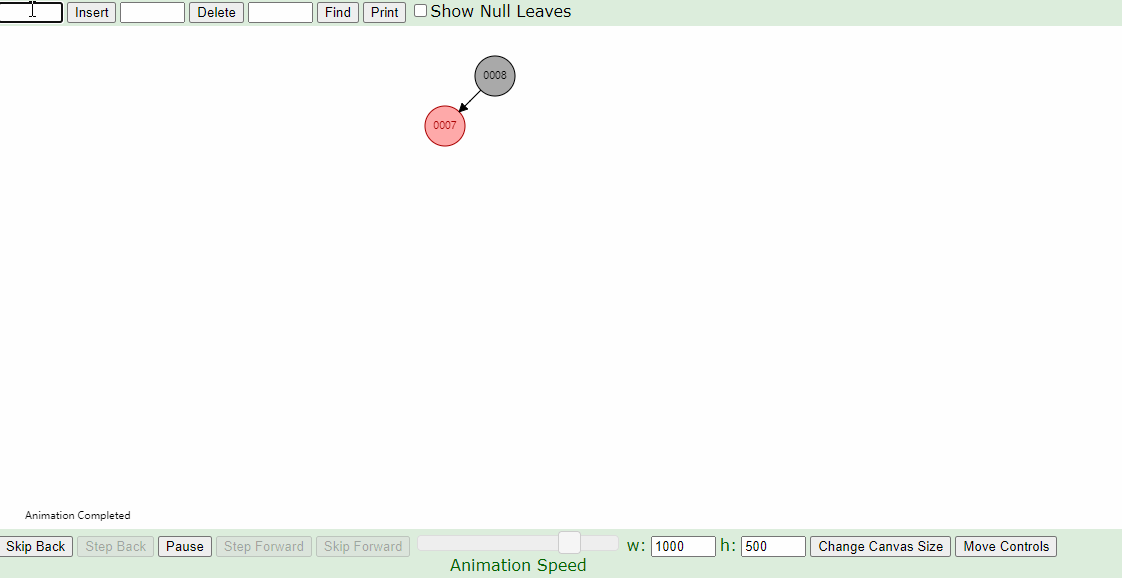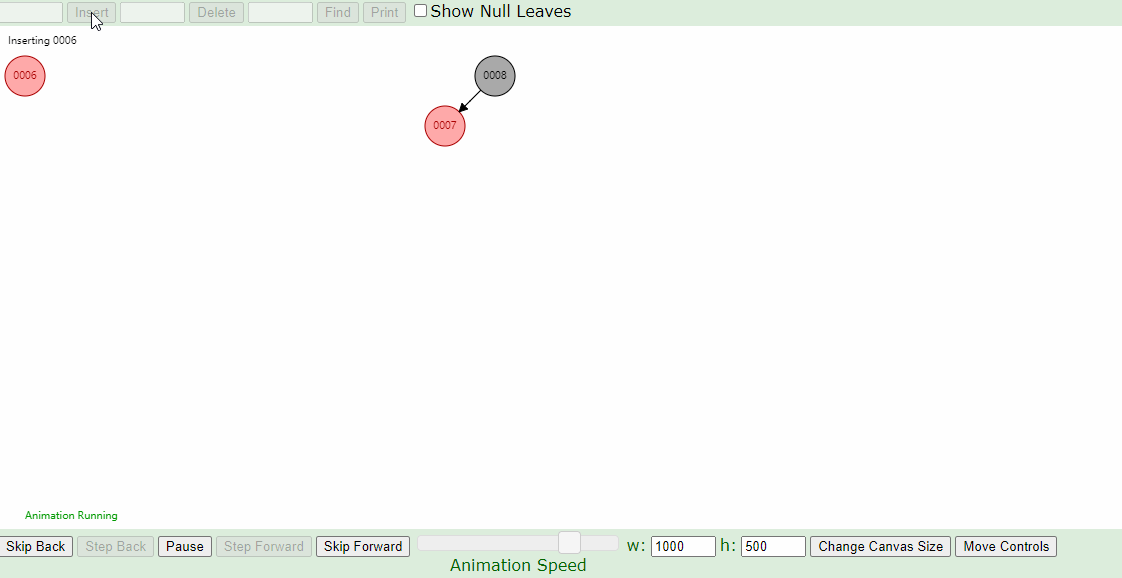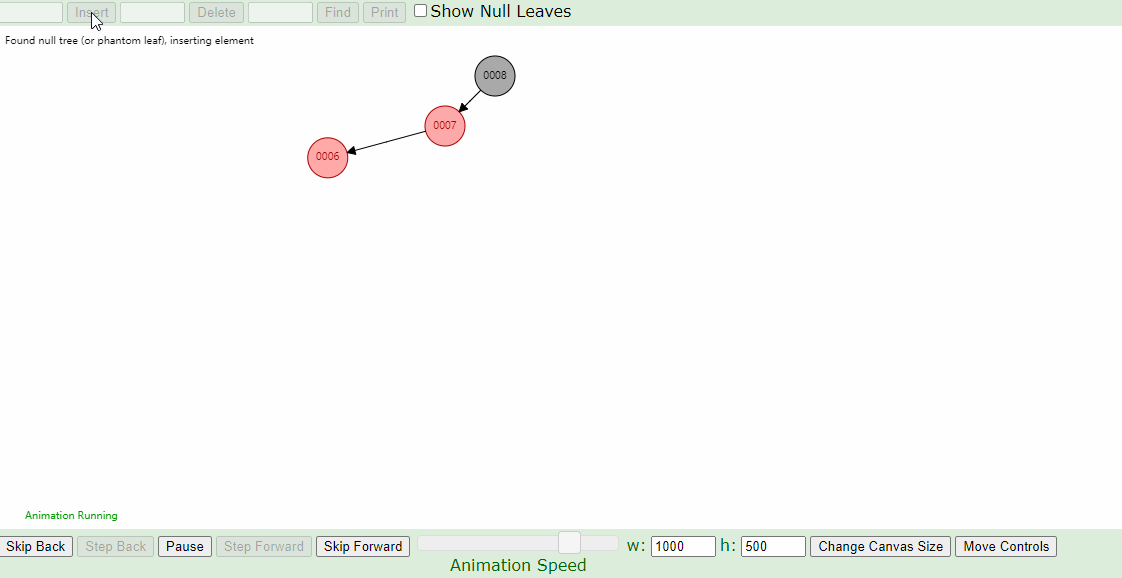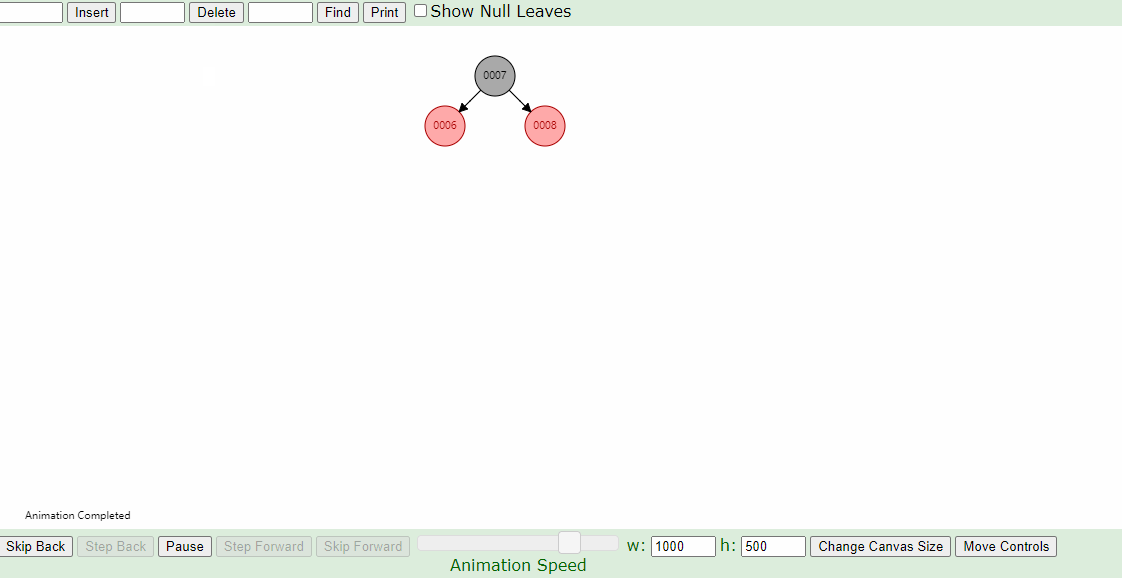
3.父亲结点为红色结点的情况下，叔叔结点也为红色结点，将叔叔和父亲结点改为黑色，爷爷结点改为红色，未完，然后又将爷爷结点当作插入结点看待，一直进行上面的操作，直到当前结点为根结点，然后将根结点变成黑色

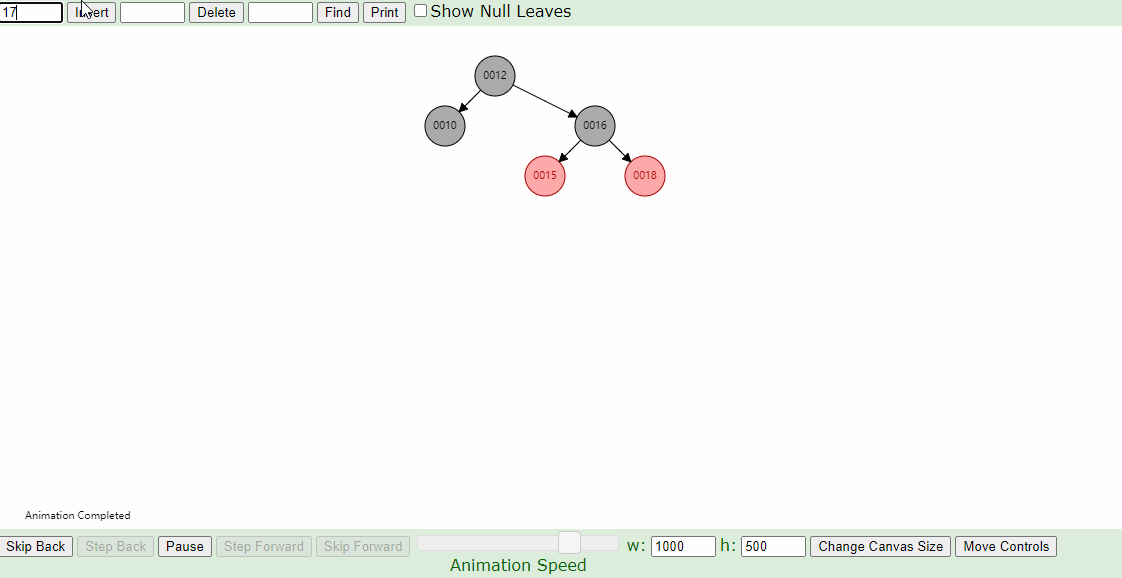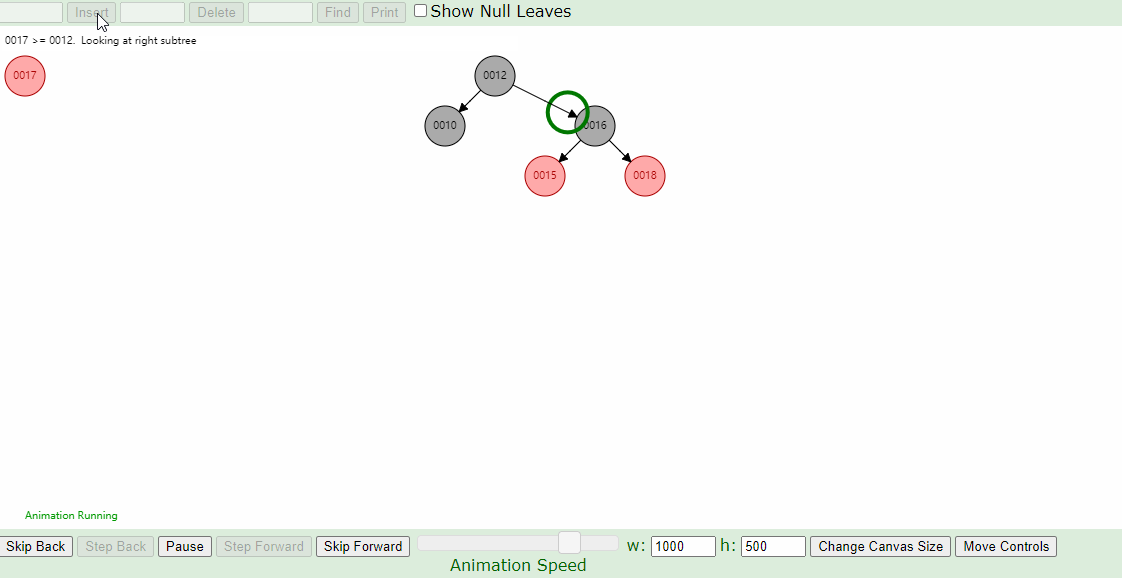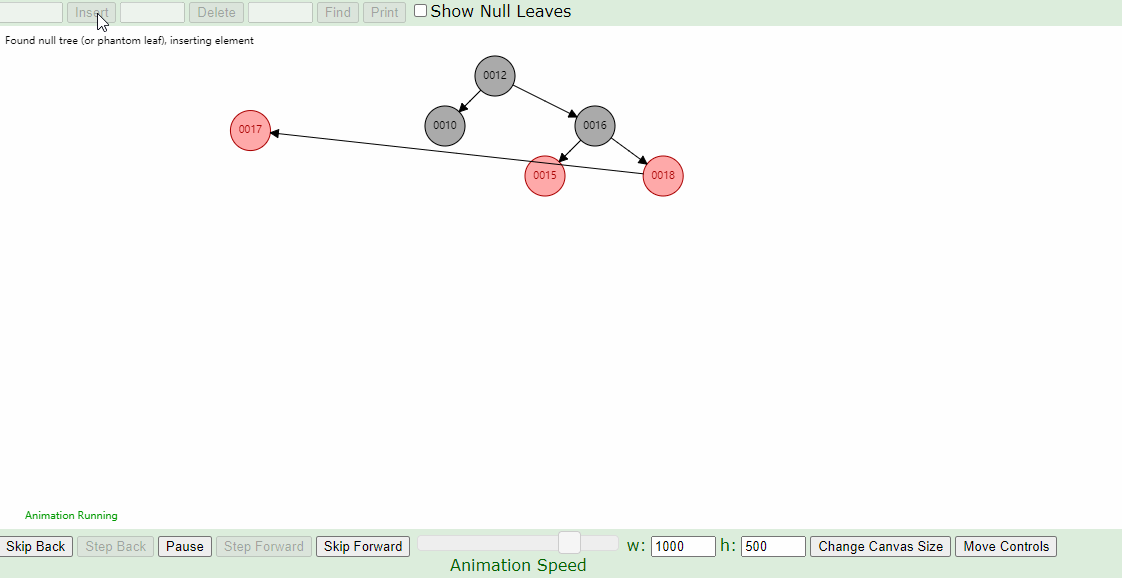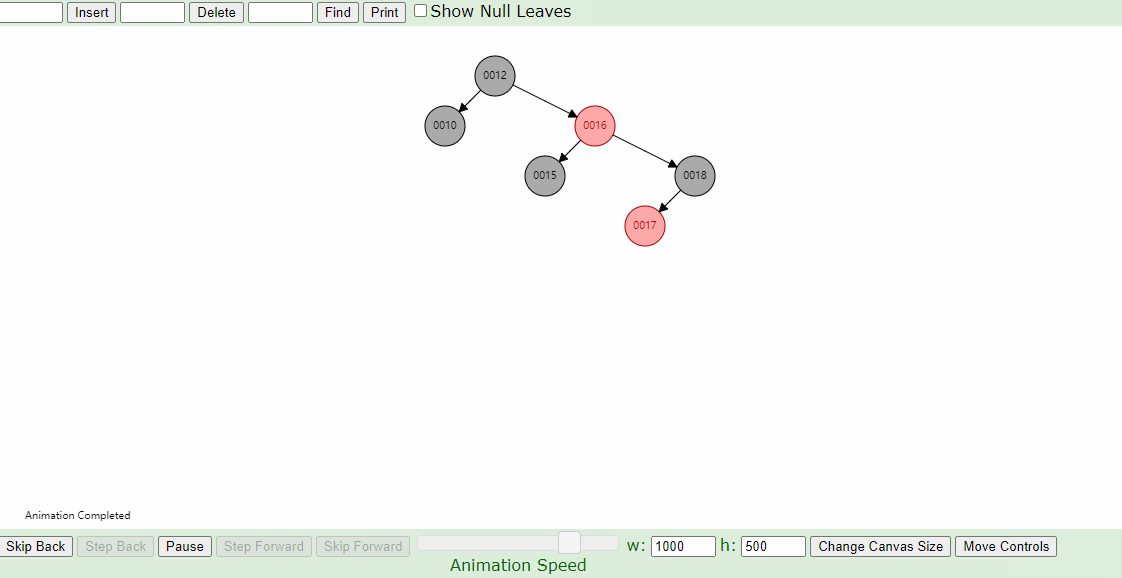
4.父亲结点为红色结点的情况下，叔叔结点为黑色结点的情况。父亲结点为左孩子，插入结点为右孩子。针对父节点进行左旋转，左旋后，必定出现2中的情况，进行相应的左旋或者右旋即可。

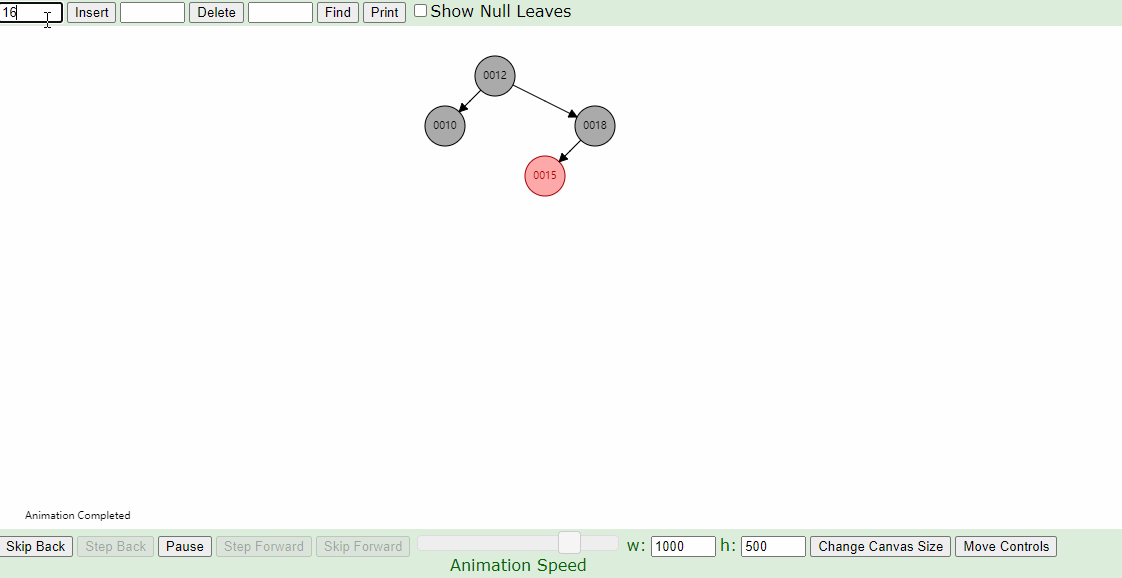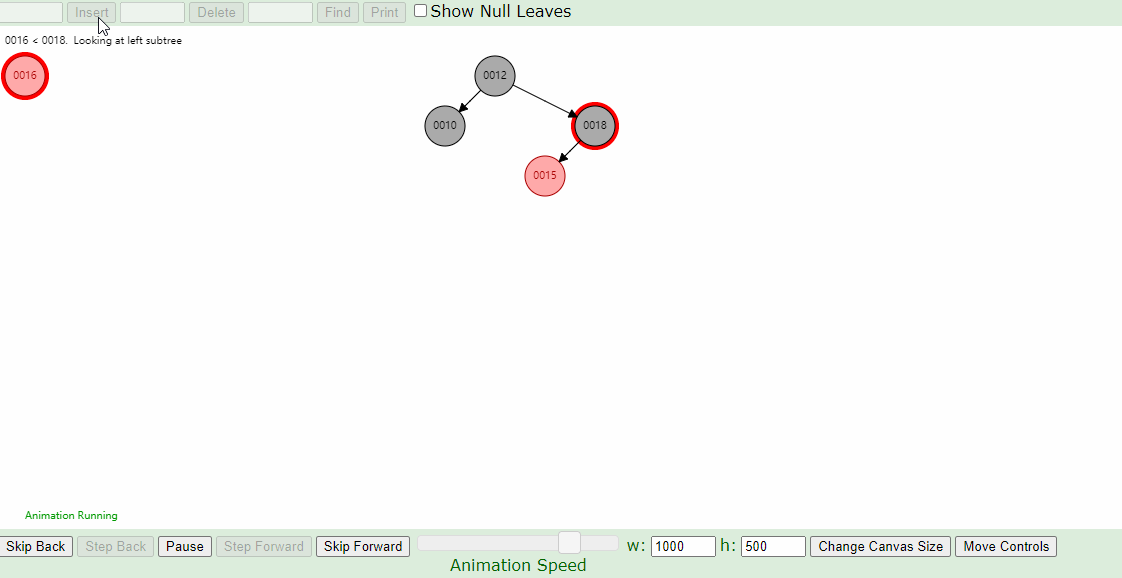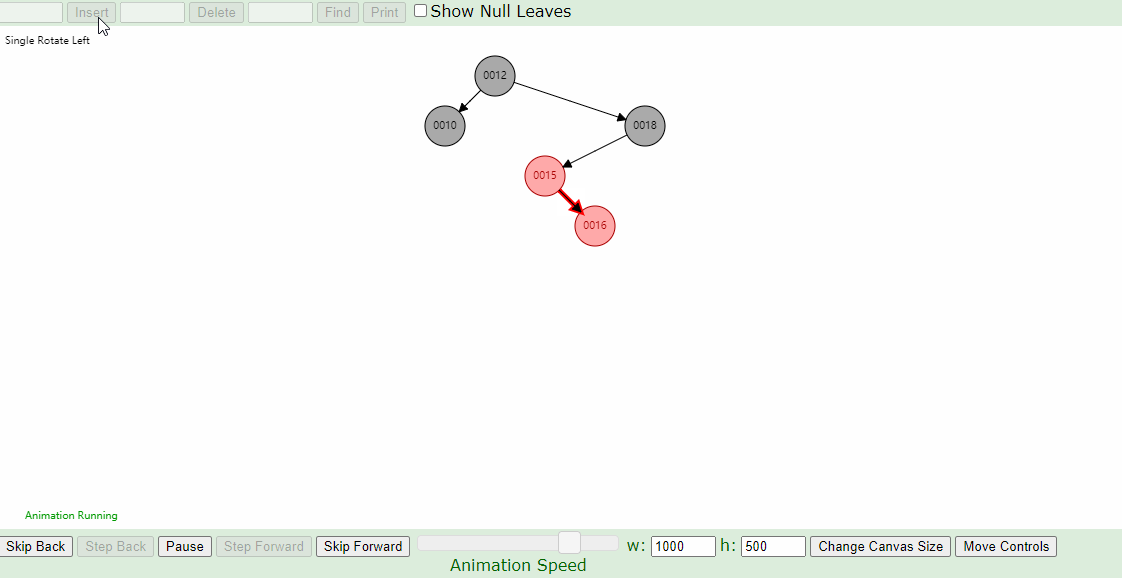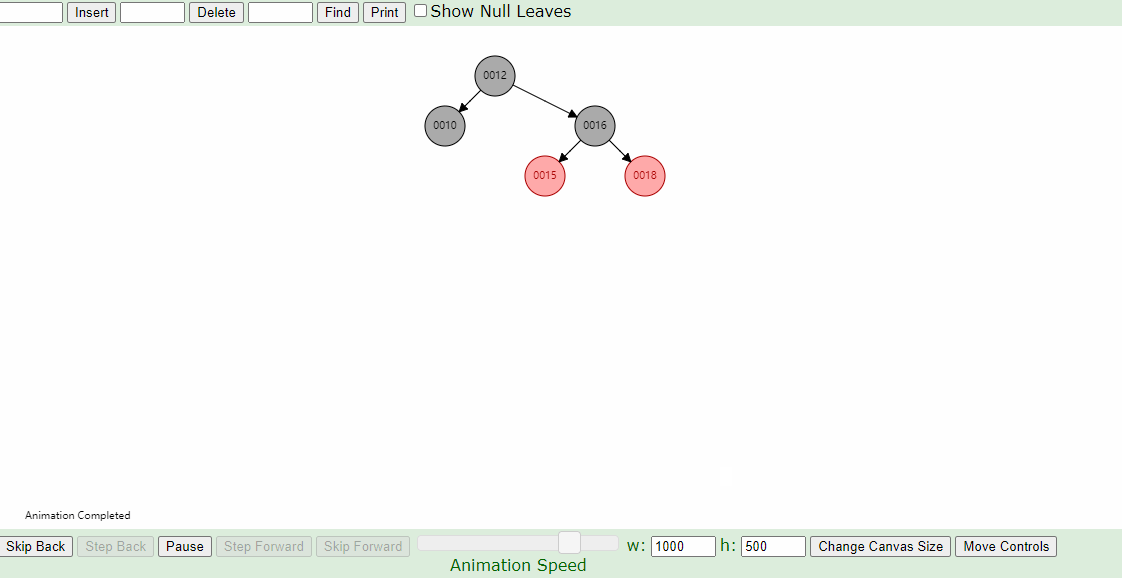
右-左，左-右的情况：

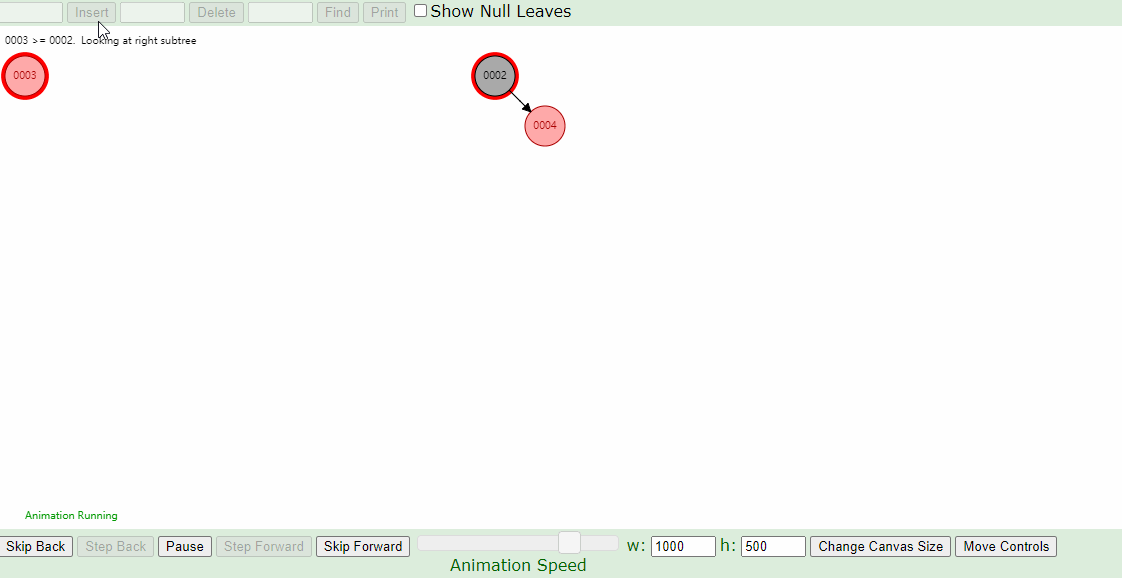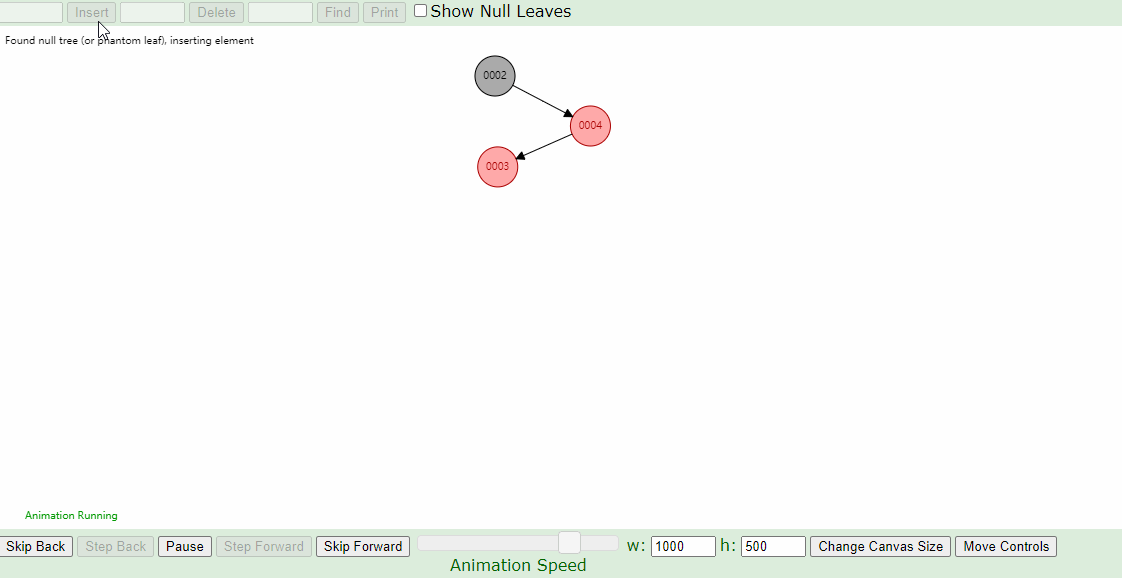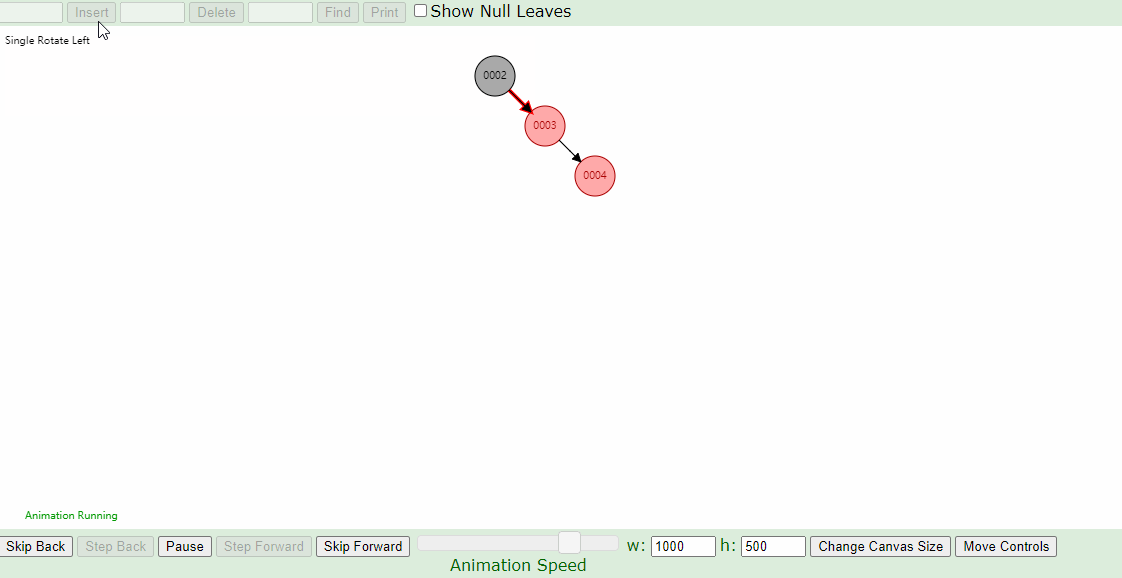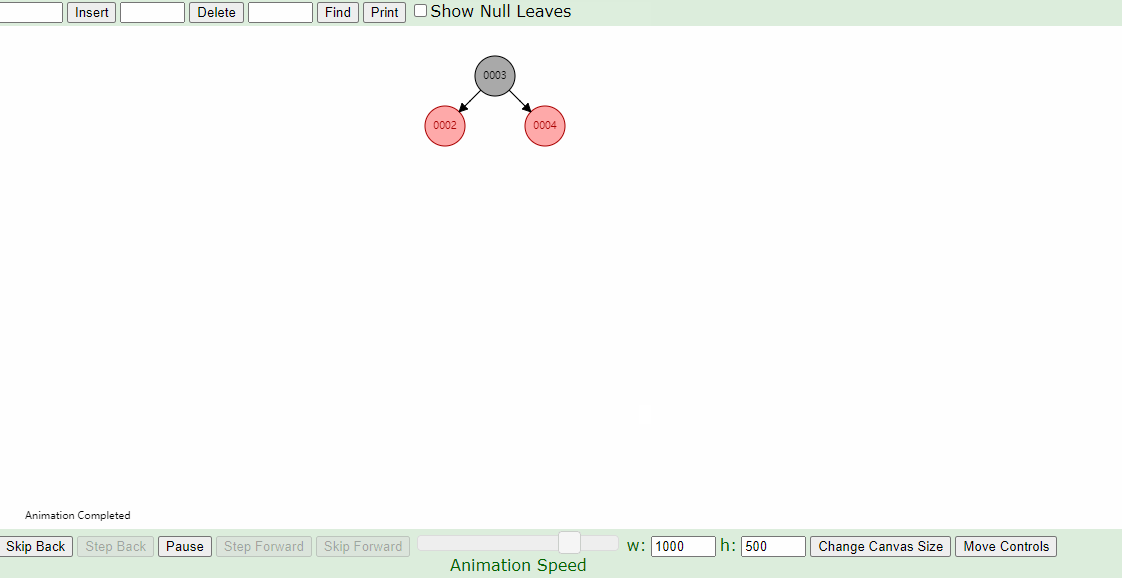
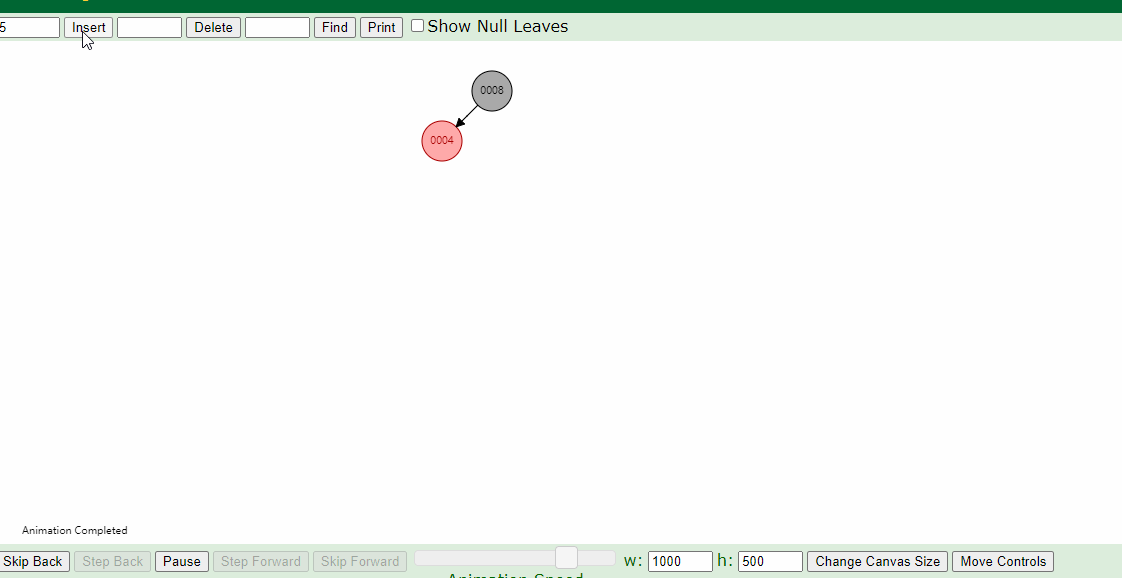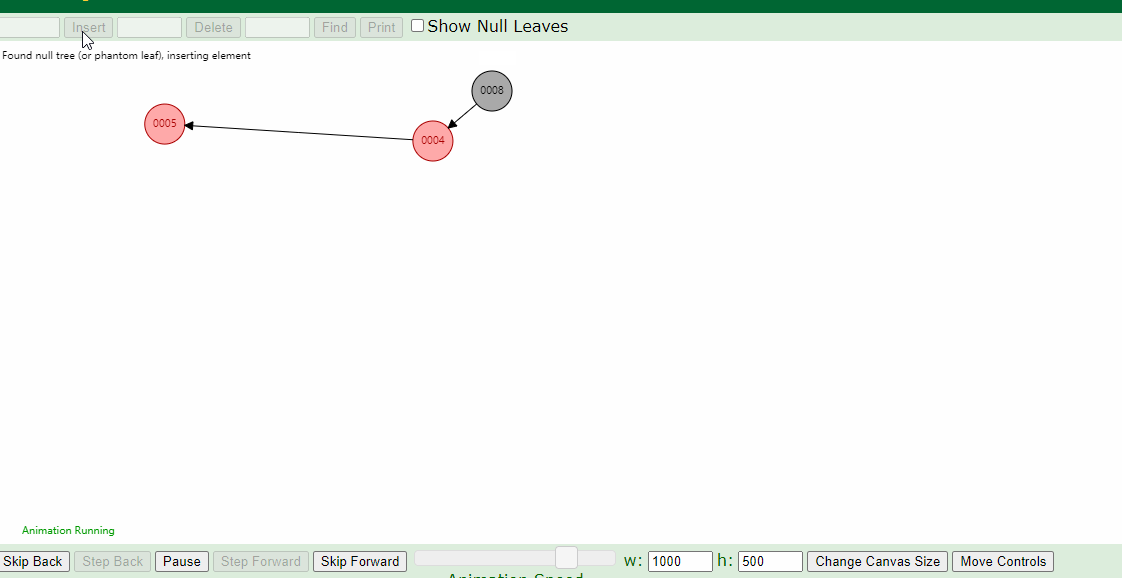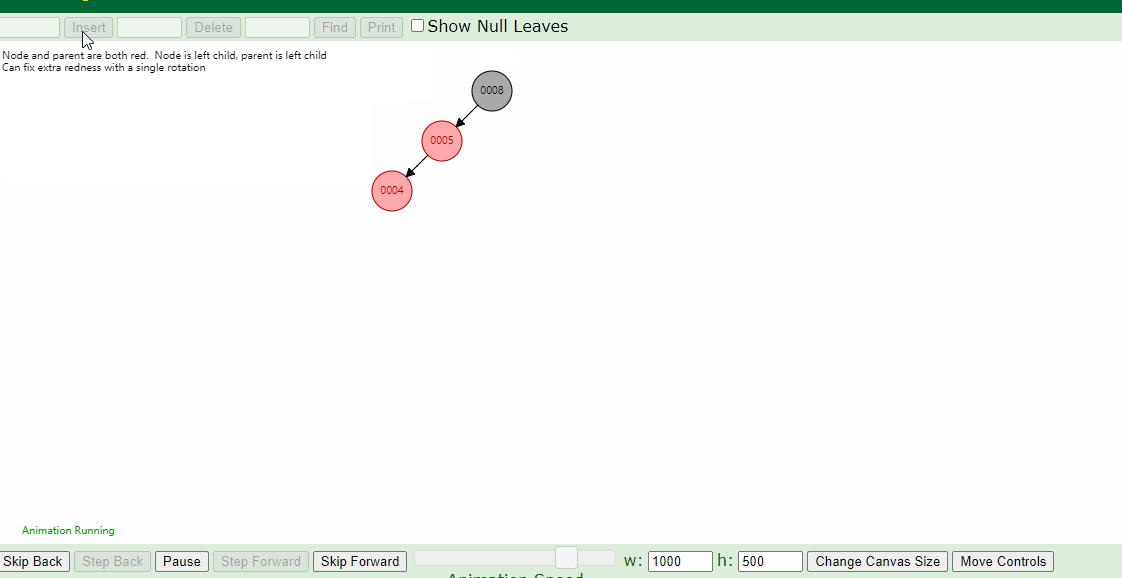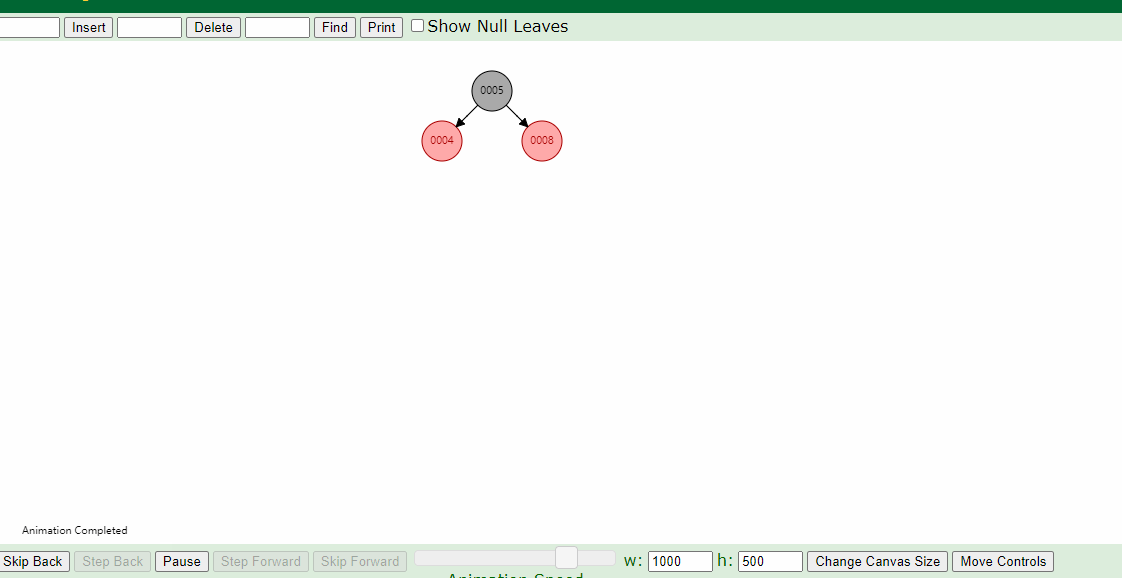
同一组数据，只是创建树的时候输入的顺序不同，它们创建的树形是一样的吗？

不是的！

比如按照1，2，3，4，5输入创建红黑树和按照5，4，3，2，1的顺序创建红黑树，它们是不同的形状：

以及：

和，3，2，4，1，5

特征1

一个显而易见的规律是，将一颗红黑数投影到下方数轴上，所有的节点都将从左到右构成一个有序组，所有目标节点的前后节点就是对应红黑数上的前继和后集节点。

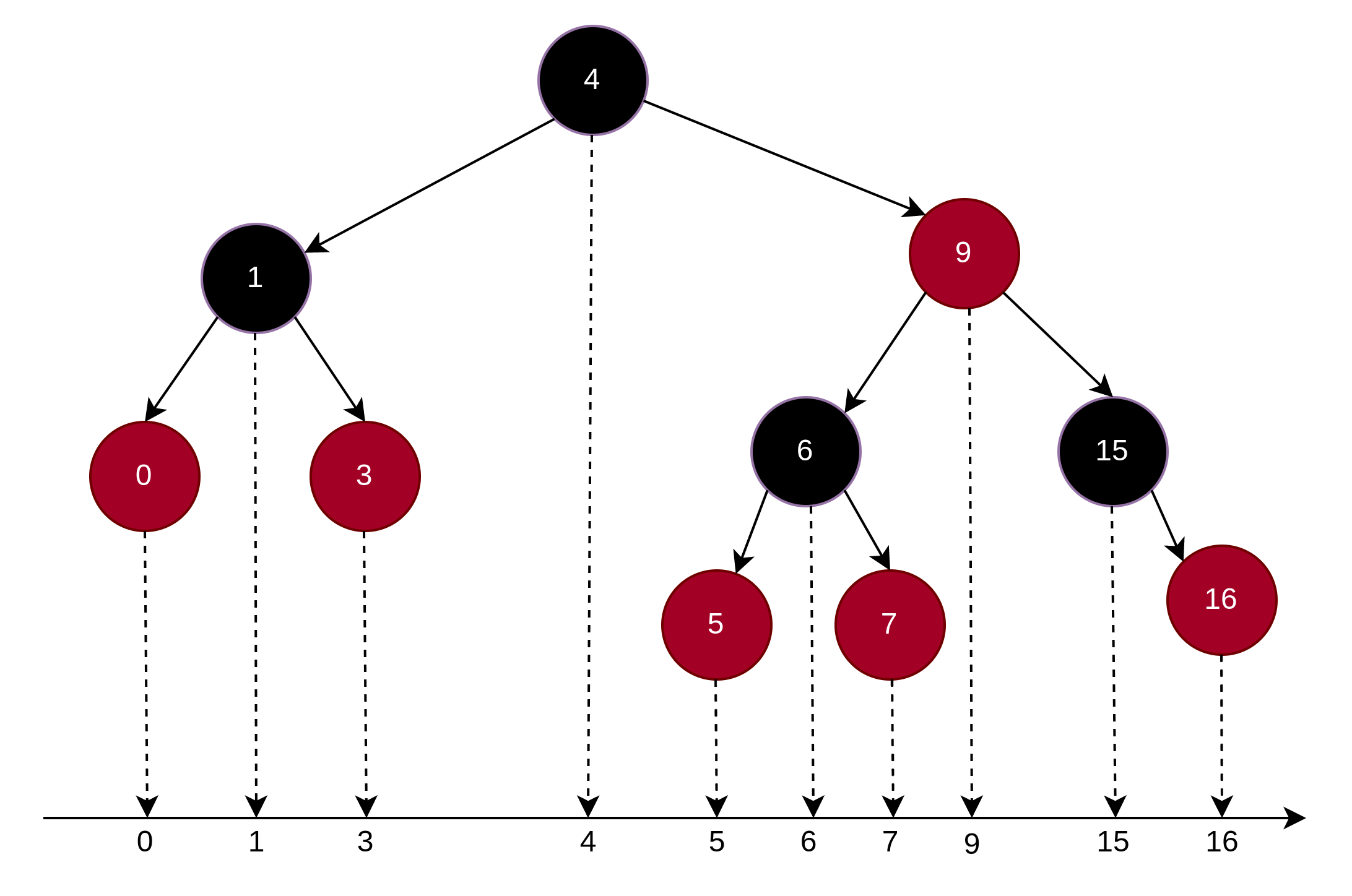
根据这个特点，如果要找一个节点的后继，只要找到这个点映射到数轴上的下一个点对应的节点就好了，具体策略上，如果这个点右子树不为空，则继续找，如果右子树为空了，说明这个分支找完了，那么就找到把这一颗子树当作左子树的节点，这个节点是整个左子树的后继。

特征2：

旋转操作只会影响子树的结构，所以旋转操作是局部的，当以便子树的节点少了，那么向另外以便子树“借”一些节点，当一边子树的节点多了，那么向另外一边子树租一些节点。

特征3：

查找，删除，插入三种操作，查找不会破坏红黑树的平衡。

特征4：

红黑树查找的时间复杂度为 $O(log^n_2)$ ,最坏情况下查找这么多次，对应的全黑平衡树或者红黑相隔的时候。所有节点红黑相隔，并且满足红黑树的定义，那么它一定是一个完全平衡二叉树的形态，所以这两个条件从形态上说都是完全平衡二叉树。没有差别。

特征5：

对于任意树，任意两个结点有且仅有唯一的一条路径联通。

特征6：

对于所有的树，如果有N个节点，那么它一定恰好有N-1条边。

特征7：

在一棵树中加一条边会构成一个回路。

特征8：

对于任意一个N个节点的数，它的度的和是 2(N-1)，证明如下：

1个节点，度和是0.

以后每加一个节点，度的和都增加2,所以是2(n-1).

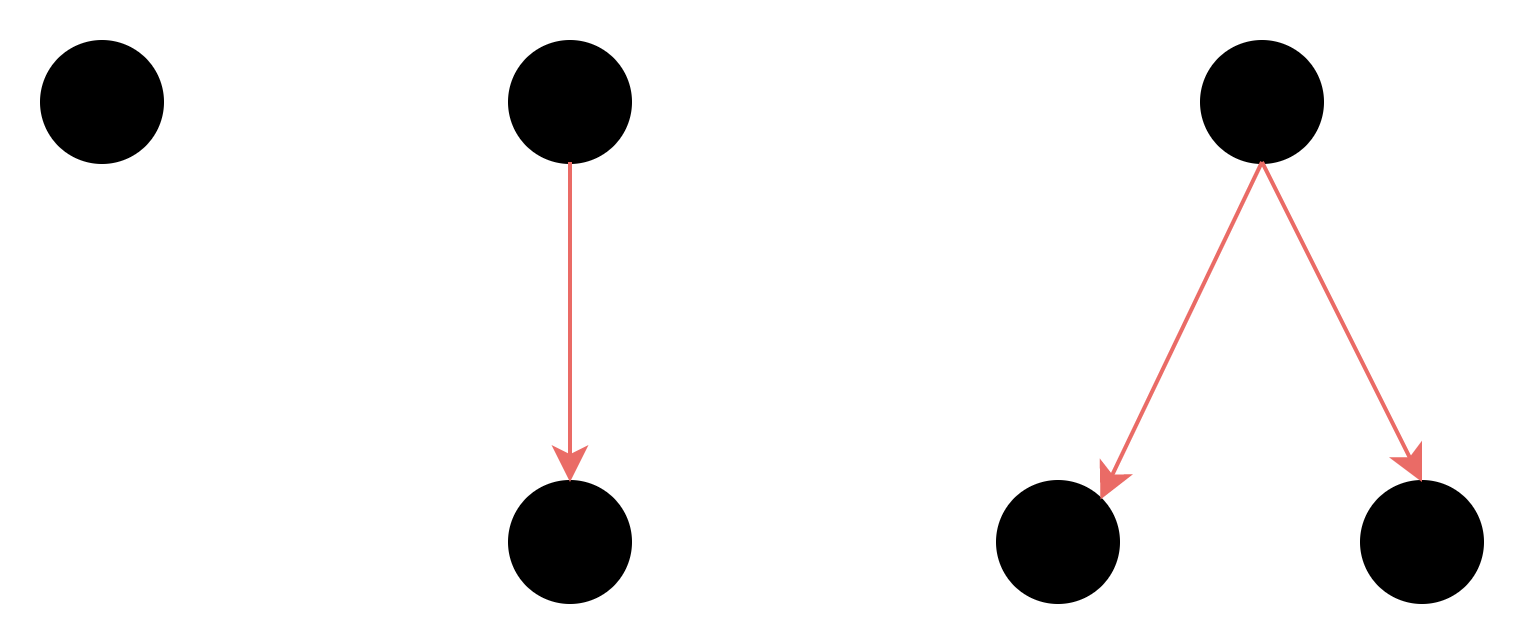
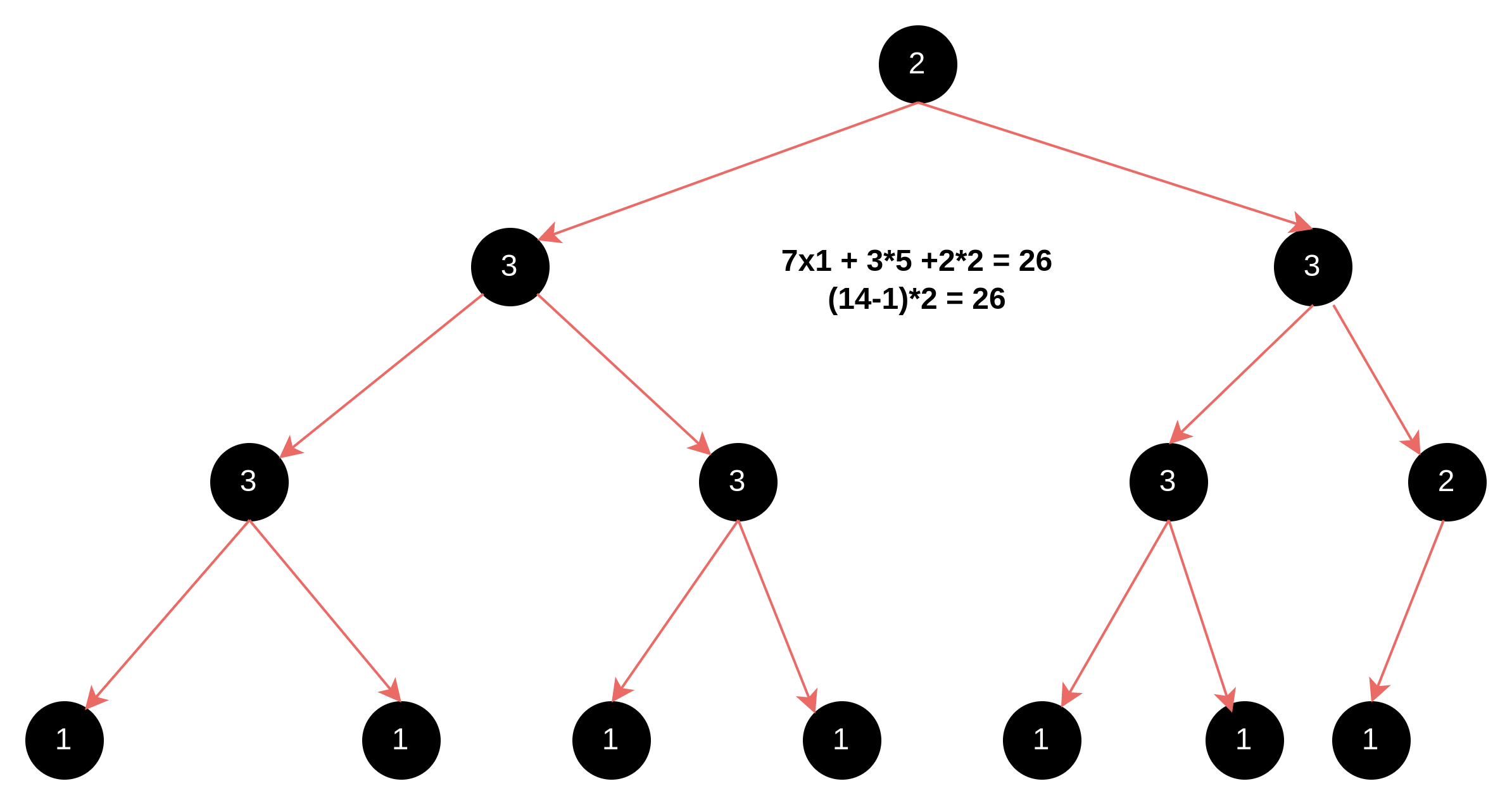
根据图论中的公式，我们计算一下树的圈复杂度，也就是被树分割成的联通区域的个数：

$V(G)=E-N+2$

E:表示边的数量，N表示节点数量，对于树来说 N=E+1. 所以，V(G) = 1，也就是树有一个连图区，这个联通区就是外部区域，所以说，树一定是没有环路的。

一张图上的封闭区域个数的计算公式为：V(G) - 1,所以树没有封闭区域。

特征9：

从树上的一个节点去往另一点，只有一条路径。反证法，如果存在第二条路径，则一定存在一条封闭路径，存在封闭面，但是前面我们已经证明了，树的结构是不存在封闭面的。

点，线，面

将一个线和点绑定理解，则点和线是一一对应的。

V（点）=E（线）

当最后一条线段结束的时候，结束的位置应该也有一个点，如下图：

也就是说，对于没有闭合的线段组，假设E表示线段个数，E表示点的个数，F表示面的个数。则对于没有闭合的连续线段来说，V=E+1,F=0.

$V-E+F = E+1-E+0 = 1$

而一段线段可以无限细分下去，每次都按照点和线对应去理解，则V+1必然E+1,所以增加线也会增加点。点的个数一定等于线的个数。

但是如果这个线逐渐闭合，则线增加，但点不会增加，而是会增加改变另一样东西的数量，就是面。

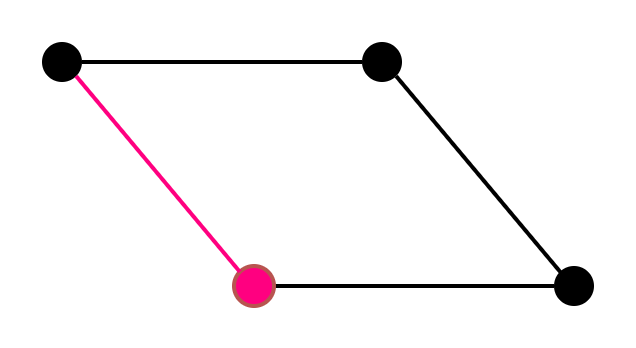
最后红色的线虽然没有创建点，但是它封闭了已经存在的一组线段，产生了面。

此时，V=4,E=4,F=1，则

$V-E+F = 4 - 4 + 1 =1$

联通性的影响：

以上规律貌似只对二维平面上的联通图才有作用，如下图所示，在虚线没有连接前：

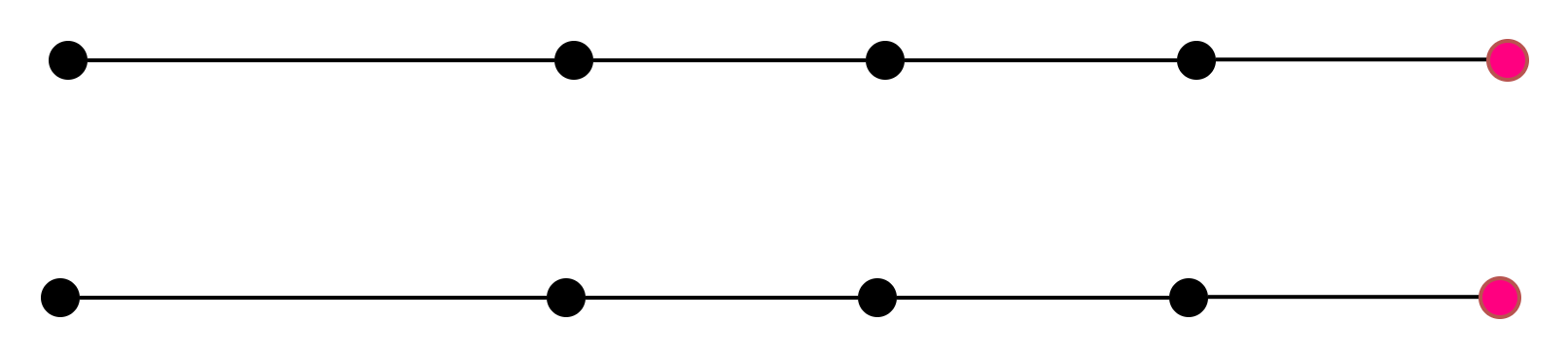
$\\ V_1 - E_1 + F_1 = 1 \\ V_2 - E_2 + F_2 = 1 \\ (V_1 + V_2) - (E_1+E_2)+(F_1+F_2)=2\neq 1$

所以不联通的情况下不满足此公式，将其联通后：

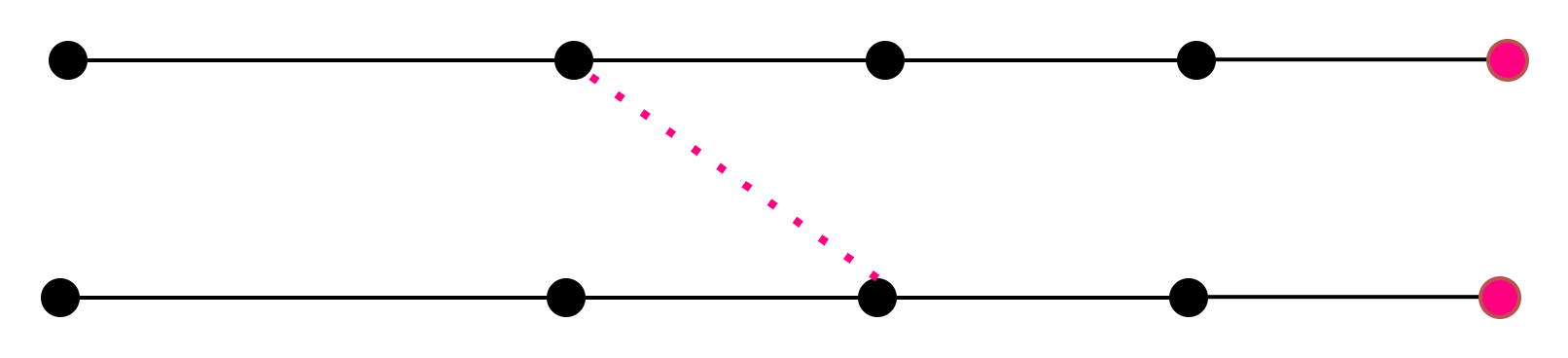
$\\ V_1 - E_1 + F_1 = 1 \\ V_2 - E_2 + F_2 = 1 \\ (V_1 + V_2) - (E_1+E_2 \mathbf{+ 1})+(F_1+F_2)=1$

局部和整体都满足了V-E+F=1的公式。

这个规律是法国数学家笛卡尔首先注意到的，后来被欧拉证明，因此这个规律被叫做欧拉定理。

和树有什么关系呢？以下面的树结构为例，E=7,V=E+1=8，则在欧拉定理约束下：

$V-E+F=1\Rightarrow F=1+E-V=1+(-1) = 0$

所以，F=0,也就是树结构的封闭面的个数为0,这就是树被称为是有向无环图的原因。

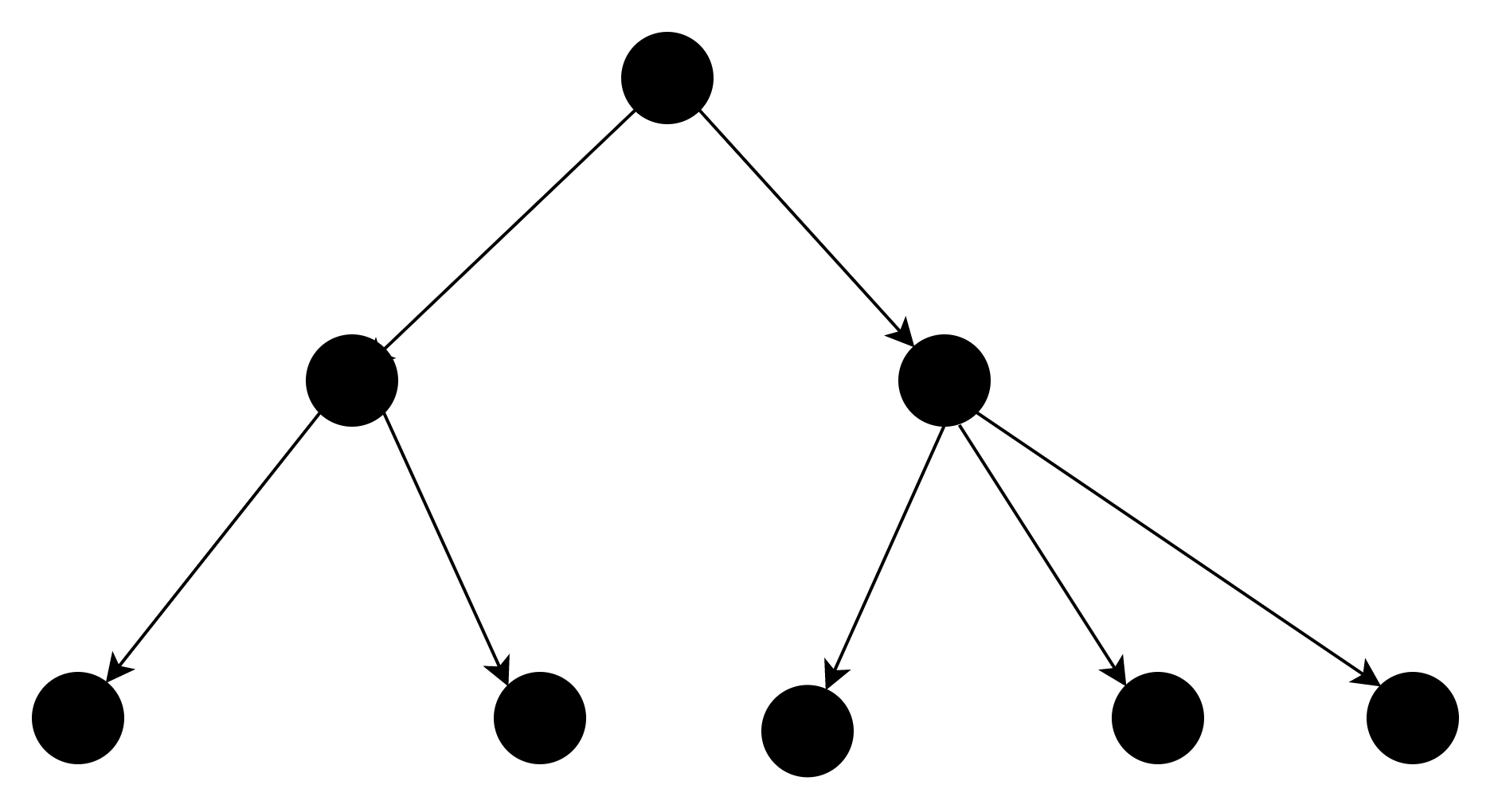
根据上面的式子，只要我们在现有节点下，连接任意两个节点构成一个边，则E加1,V不变，F变为1,也就是说，树只要在加上一条边，就可以构成一个面（环），这也是树的的一个非常重要的特点，正经的树不会有环结构。如果把地球看成根节点，排除地球，则树枝的数量等于树叶的数量加上树杈的数量。

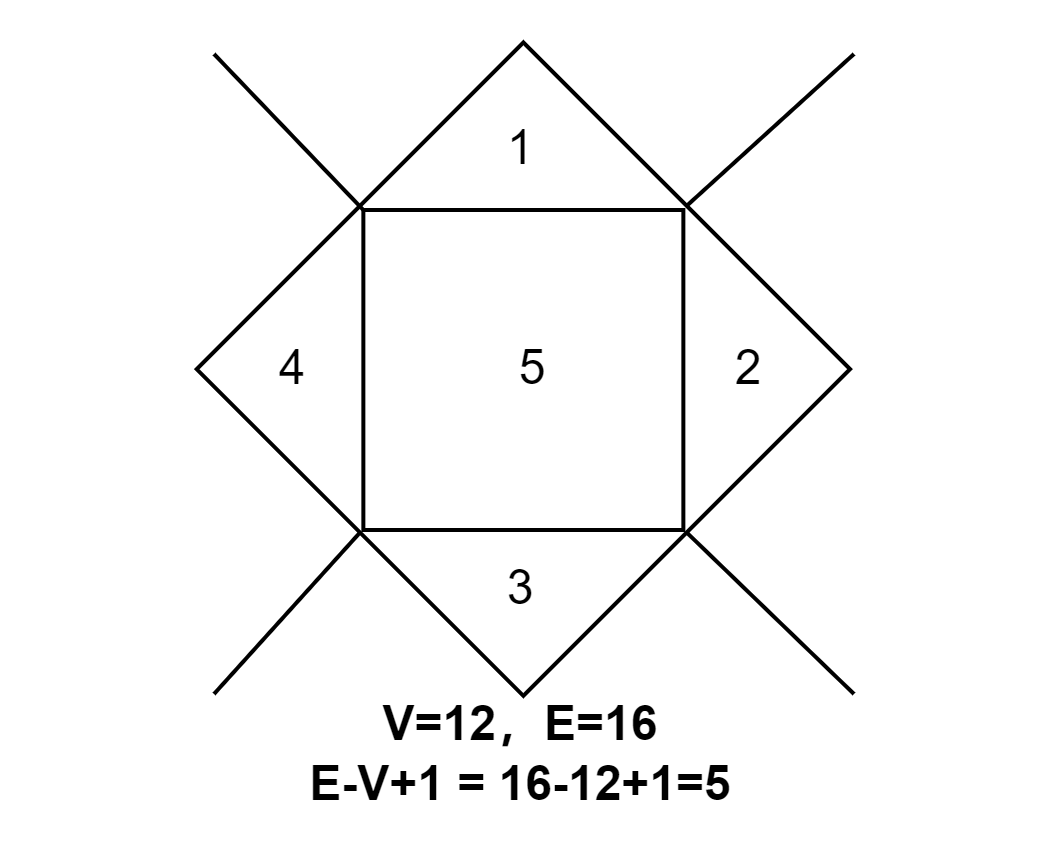
在用另一个简单的矩形来验证欧拉定理：

矩形有4个顶点，4条边，则根据欧拉定理 F=E-V+1 = 4-4+1=1个封闭面，和实际吻合。

如果增加一个对角线，也是吻合的，有两个面：5-4+1=2.

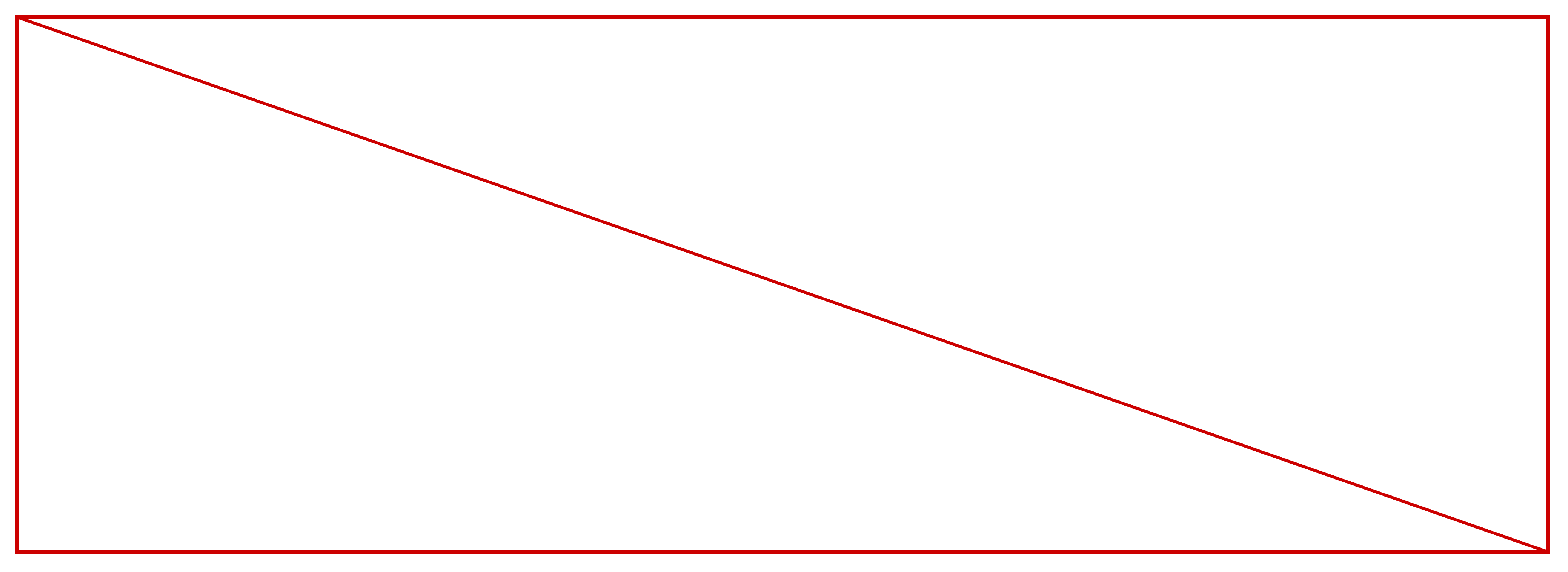
如果有再加一个对角线，将会发生根本性变化，此时有四个面，但是却不满足6-4+1=3个面的要求。

有这样的例外是因为新的图形已经不是普通的平面图了，而是带有通孔的形状，你可以想象把下图以虚线为把守提起来，则把手和下面矩形图形之间存在一个孔洞。对于这种形状，欧拉定义要换以下形式：V+F=E+1-2N，其中N为通孔的数量，这里为1,所以公式实际上是V+F=E-1.

~~代入验证，V=4,E=6,F=3，貌似也不对。~~

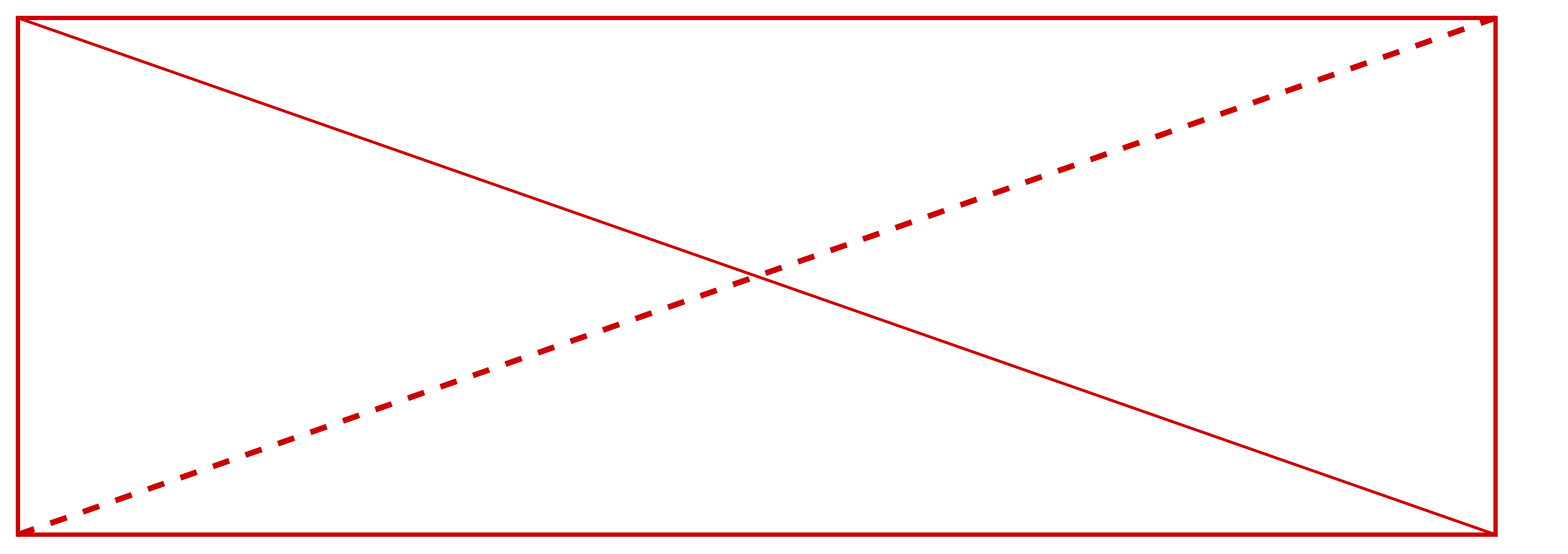
怎么理解第二个对角线呢？或许可以这样理解，将左下角的顶点缩进矩形里面，然后新增加的对角线不和第一条对角线相交，这个时候，V=4,E=6,E-V+1=3，实际上也有三个独立的面。仍然满足二维平面的欧拉定理。

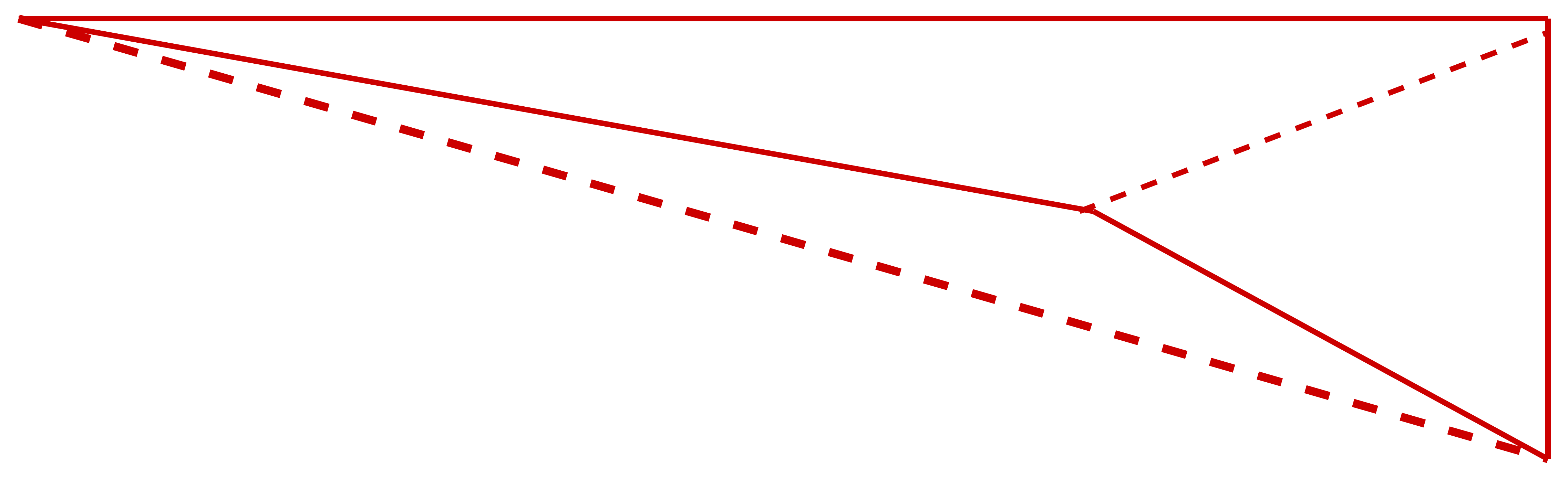
这里的面理解成面积是可以的，如果新的线没有增加表面积，就需要稍微调整一下拓扑，比如上面的第二个对角线，如果按照变换前的方式去理解，你会发现新增两个面，但实际上这两个面和第一条对角线分出来的两个面面积是重合的，没有新增加面积，所以需要将一个顶点缩进去，让第二条对角线新增加的面显示出来。

和程序流程图有什么区别？

程序流程图不会有那么多的结束节点，流程图只有一个开始和一个结束，所以流程图一定是有方向，有环路的。但是程序流的执行部分和树结构也有相似性。比如,程序流每个节点也是单入多出的。

既然有相似性，这里思考怎样花最小的代价让一个树变成程序流程图?仅仅从形式上考虑，不考虑程序逻辑，如下图所示，感觉这是一个比较好的方法：

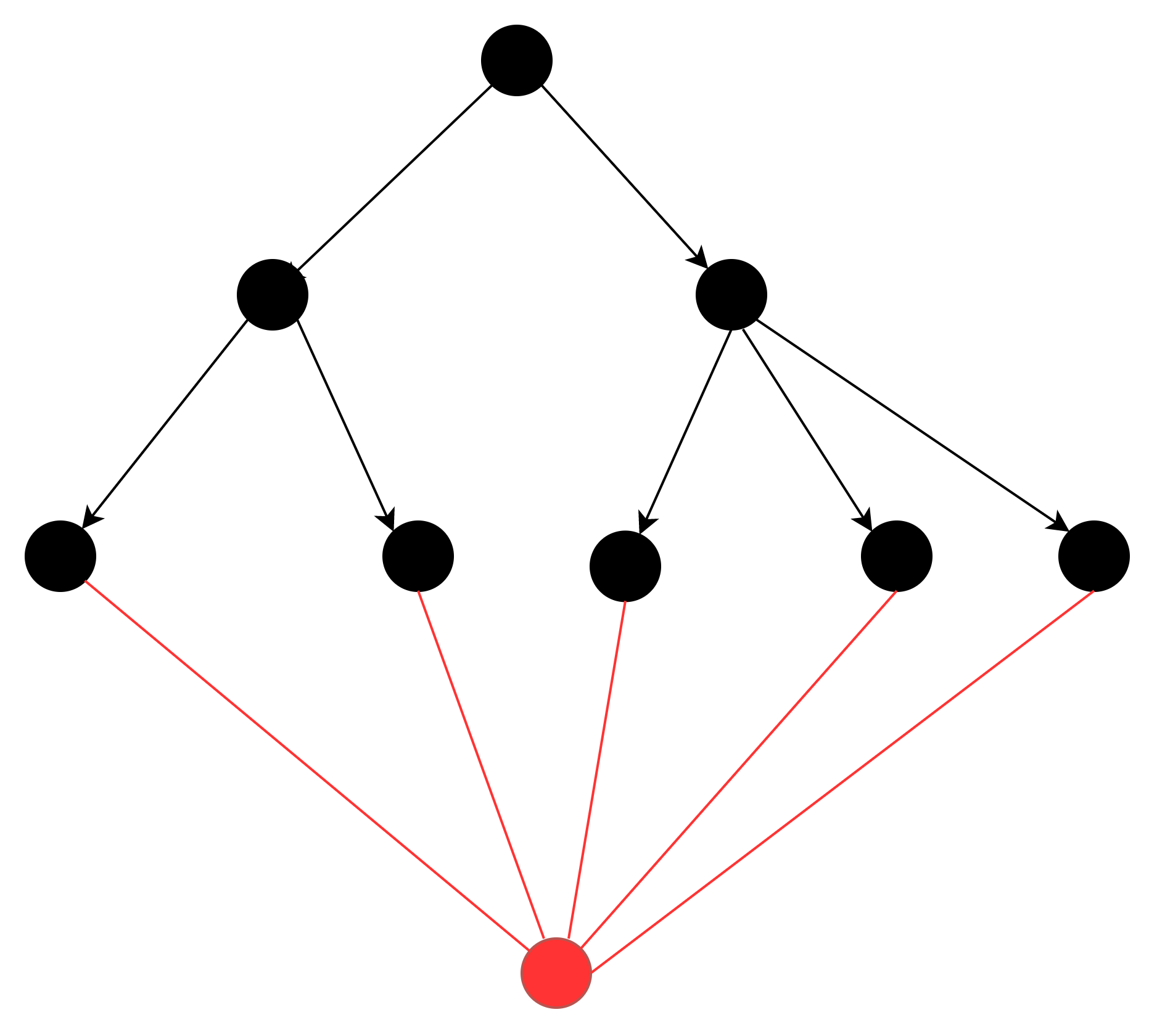
方法是，在原来树的基础上，增加一个结束节点，然后依次连接每个叶子节点和结束节点。让所有的中途节点都倒龙入海，引火归元。

由于在原来的条件下，已经满足V-E+F=1.此时在加上1个结束节点和叶子数个边，设叶子个数为Y。

V+1-(E+Y）+F`=1=>F`=E+Y-V=Y+E-V=Y-1.

也就是这样操作后，面的个数从0变为Y-1个，也就是说，面的个数变为了叶子树减1.这个其实很好理解。不考虑树的上面部分结构，单纯从叶子节点考虑，相邻区间的个数是节点数-1,这个容易理解的。

程序流程图可以堪称是球面南北极之间无数条路径在二维平面上的展开，中间每一次的选择分岔都要在终点相遇，构成为一个封闭区域。

上海大世界天桥石柱上的图形

假设有n个顶点的全链接图，有几个平面？

根据欧拉定理：

V=n

E=(n-1)+(n-2)+...+1 = n(n-1)/2

$F=E-V+1 = \frac{n^2-n}{2}-n + 1=\frac{n^2-3n+2}{2}=\frac{(n-1)(n-2)}{2}$

我们分别代入几个点数验证一下，3个点构成一个一个面，F=1.

四个点的情况F=3，满足。

换另一种解题思路,3个点构成一个面，我们看N个点能选择几个3点组合，把几何问题转化为排列组合问题。

$C^3_n = n(n-1)(n-2)/6$

当N=4的时候，后者是C(4,3)=4. 而前者是3，所以排列组合方式是错误的。

实际上，排列组合的方式的计算公式应该是：

$C^2_{n-1} = \frac{(n-1)(n-2)}{2}$

和第一种方法推到出来的公式精确吻合,至于为何，细细思考。比如四个点的全连接(其实就是上面矩形用例的变形).我们不需要关注中间节点,只要关注围绕中间节点的剩余节点之间互联就可以了.

这种方法是全相联吗? 是的,我们可以验证一下,总的线数为:

$C^2_n=\frac{n(n-1)}{2}$

而根据第二种方法计算:

$C^2_{n-1}+n-1 = \frac{(n-1)(n-2)}{2}+(n-1) = \frac{n(n-1)}{2}$

两相吻合,所以实际上后者也是全连接.

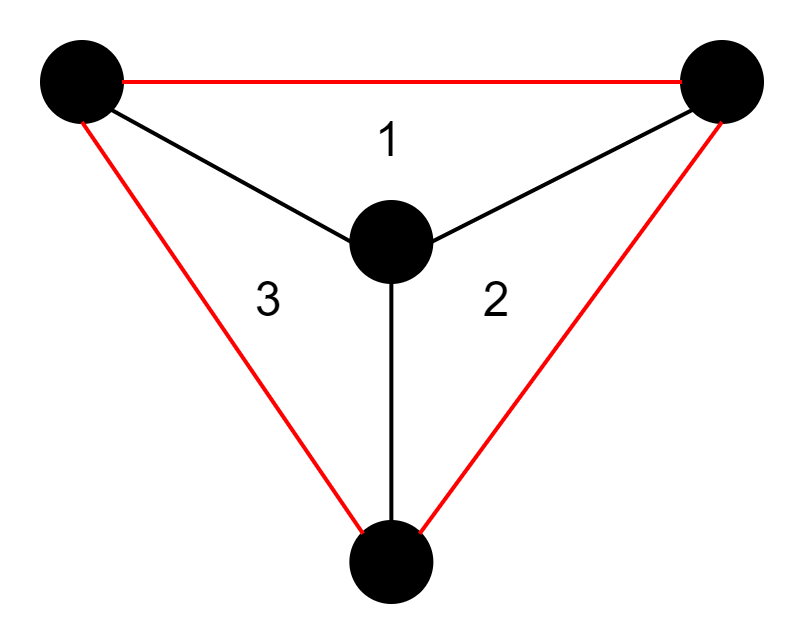
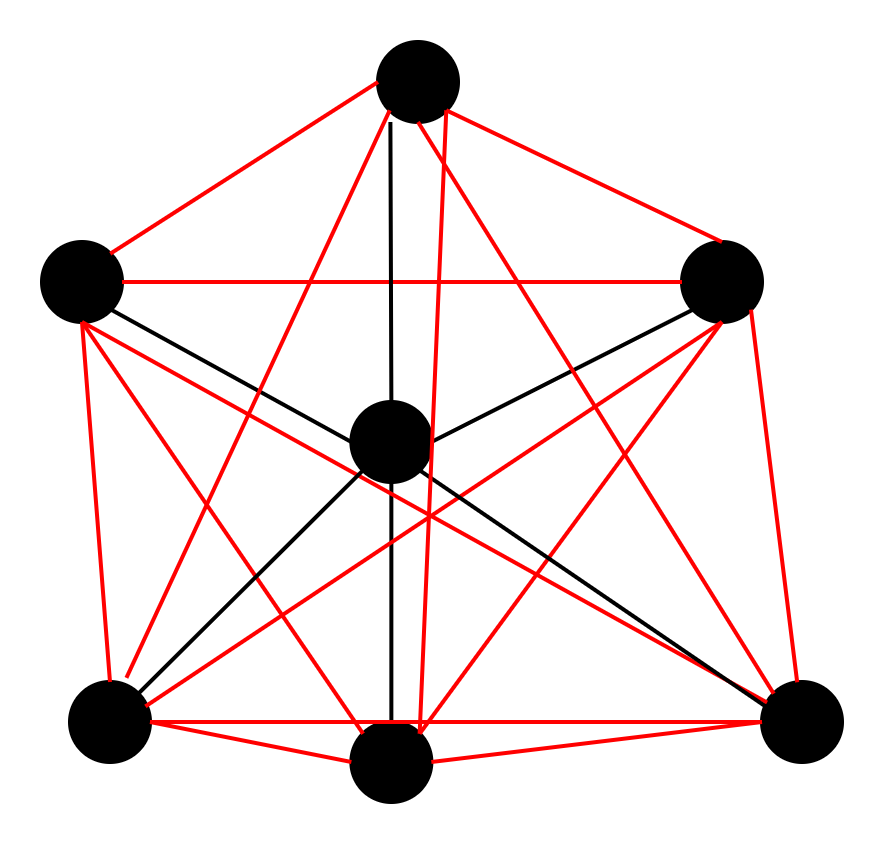
一笔画图形

判断一笔画图形的方法：能一笔画成的图形上的点，除了起点与终点以外，每个点都应该与偶数条线相连，这种点叫偶数点。与奇数条线相连的点叫奇数点。能一笔画成的图形中除了起点与终点以外不应有奇数点。
所谓“一笔画成”规律，即一个图形从起点到终点可由一笔画成而线路不中断。一笔画中，点可以重复但线不可以重复。“偶点”，即交点处所连接的线条数位偶数；“奇点”，即交点数所连接的线条数为奇数。
1、只有偶点，可以一笔画，并且可以以任意一点作为起点。
2、只有两个奇点，可以一笔画,但必须以这两个奇点分别作为起点和终点。
3、奇点超过两个，则不能一笔画。对于一些比较复杂的路线问题，可以先转化为简单的几何图形，然后根据判定是否能一笔画的方法进行解答。

一笔画完,中间节点必须为偶数度,开始和结束可以为奇数度.数有多个奇数度,所以树不能一笔画完.

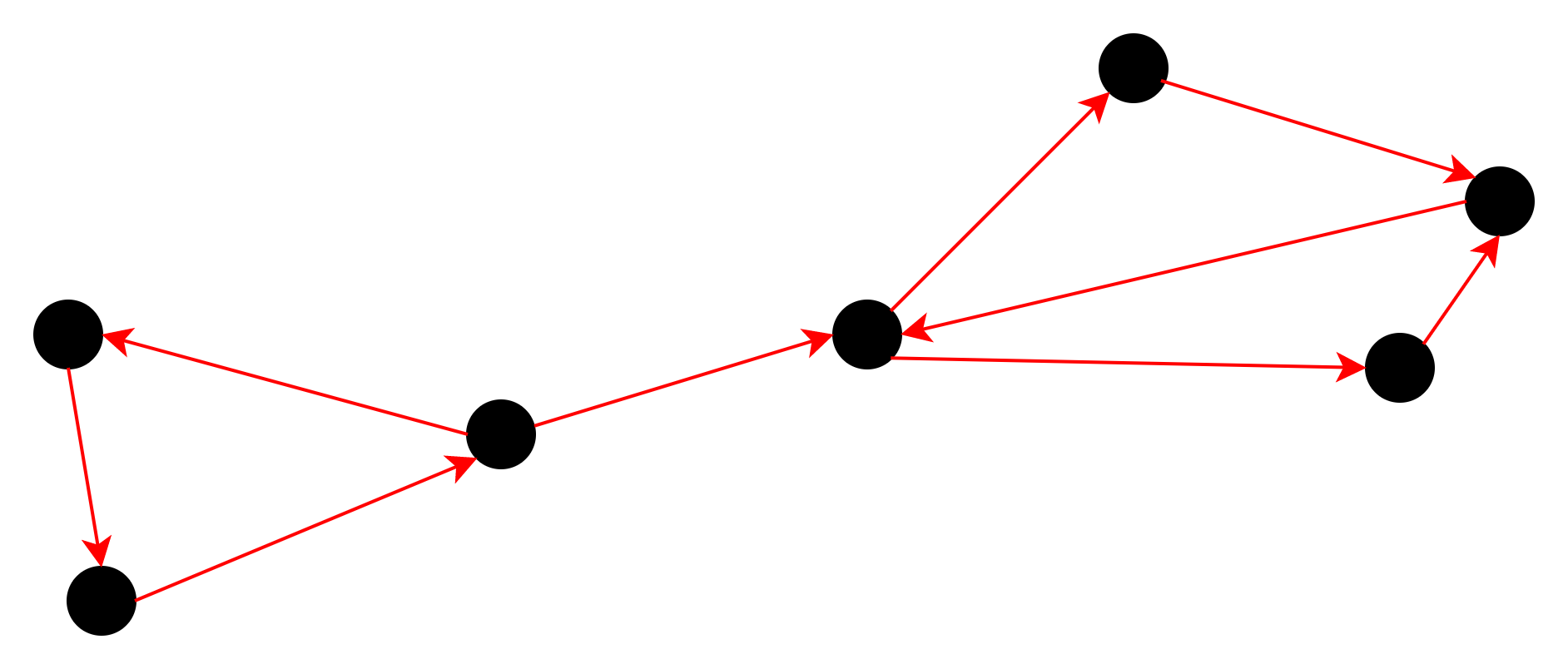
树有面积吗?

根据前面用欧拉定理得到的结论,树没有闭合平面,何来面积?

回路

一个图中，起点和终点相同的路径称为回路。

割边：割边_百度百科

红黑树的插入合并

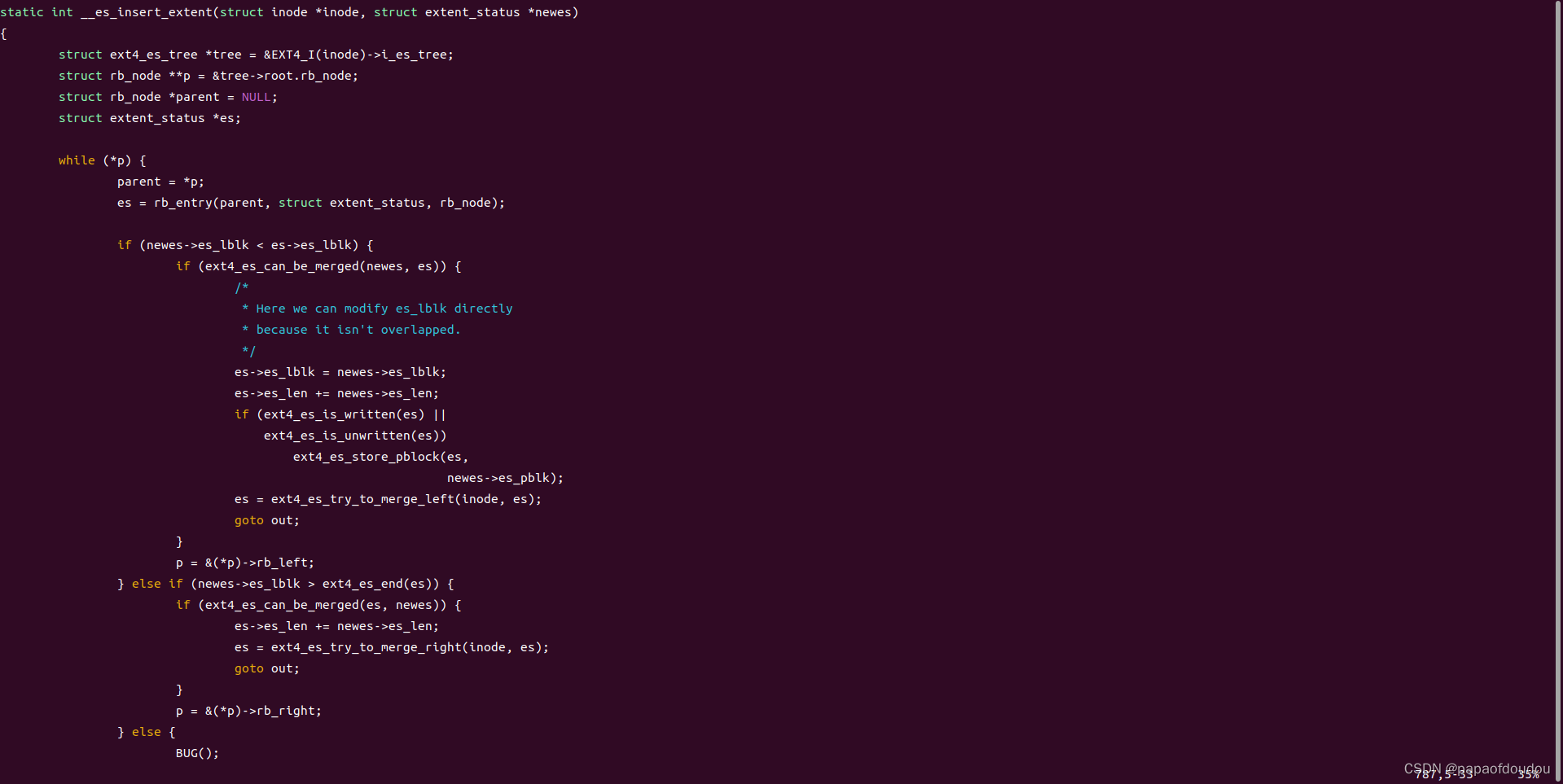
参考内核如下代码：

struct bo_va_map {struct rb_node rb;struct rb_root *root;void  *cookie;uint64_t start;uint64_t len;uint64_t flags;
};struct rb_root bo_va_map_free_root = RB_ROOT;
struct rb_root bo_va_map_busy_root = RB_ROOT;
int rb_tree_mem_bo_insert(struct bo_va_map *map)
{struct rb_root *root = map->root;struct rb_node **tmp = &root->rb_node, *parent = NULL;#if 0/* Figure out where to put new node */while (*tmp) {struct bo_va_map *this;parent = *tmp;this = rb_entry(parent, struct bo_va_map, rb);if (this->start > map->start)tmp = &(*tmp)->rb_left;elsetmp = &(*tmp)->rb_right;}
#elsestruct bo_va_map *this, *prev, *next;struct rb_node *node;while (*tmp) {parent = *tmp;this = rb_entry(parent, struct bo_va_map, rb);if (map->start < this->start) {if (map->start + map->len == this->start) {this->start = map->start;this->len += map->len;node = rb_prev(&this->rb);if (!node) {return 0;}prev = rb_entry(node, struct bo_va_map, rb);if (prev->start + prev->len == this->start) {prev->len += this->len;rb_erase(&this->rb, this->root);kfree(this);}return 0;}tmp = &(*tmp)->rb_left;} else if (map->start >= this->start + this->len) {if (map->start == this->start + this->len) {this->len += map->len;node = rb_next(&this->rb);if (!node) {return 0;}next = rb_entry(node, struct bo_va_map, rb);if (this->start + this->len == next->start) {this->len += next->len;rb_erase(&next->rb, next->root);kfree(next);}}tmp = &(*tmp)->rb_right;} else {BUG();return -1;}}
#endif/* Add new node and rebalance tree. */rb_link_node(&map->rb, parent, tmp);rb_insert_color(&map->rb, root);return 0;
}

红黑树插入MERGE检查需要检测两次，分别要和前面的节点（如果有）和后面的节点（如果有）各检查一遍。