本文主要是介绍消消乐算法总结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
最近在工作中遇到一个问题,做一个消消乐的demo项目,连续相同数目超过四个后就要消除。我在网上看了很多解决方案,有十字形,横向,纵向,梯形搜索。越看越迷糊。这不是用一个BFS就能解决的问题吗?为什么要设定这么多情况?难道是为了优化吗?但是用BFS的同时用一个矩阵记录已经寻找过的元素不就可以提高效率吗?鉴于网上的解决方案如此的低级,还有的需要收费,或者说我没有找到。所以今天我就讲讲我的解决方案并附上代码,希望能有人从我的文章获得收益。消消乐其实也就是两个算法的组合:消除算法,填充算法。
消除算法
先讲讲我的思路:
- 生成随机矩阵,虽然网上有一大堆说生成的矩阵不能直接消除,所以又会有算法来解决这个问题,这里我就不说了,我就用随机生成的矩阵吧。
- 遍历矩阵中的每一个元素
- 对每一个元素利用BFS进行寻找周围四个方向的元素,同时在遍历的过程中需要进行过滤,防止对一个元素进行重复便利最终导致死循环。
var gameMatrix = new Array(4).fill(0).map(()=>new Array(4).fill(0));
!function createData(){for (let i = 0; i < 4; i++) {for (let j = 0; j < 4; j++) {this.gameMatrix[i][j] = Math.ceil(Math.random()*5)}}
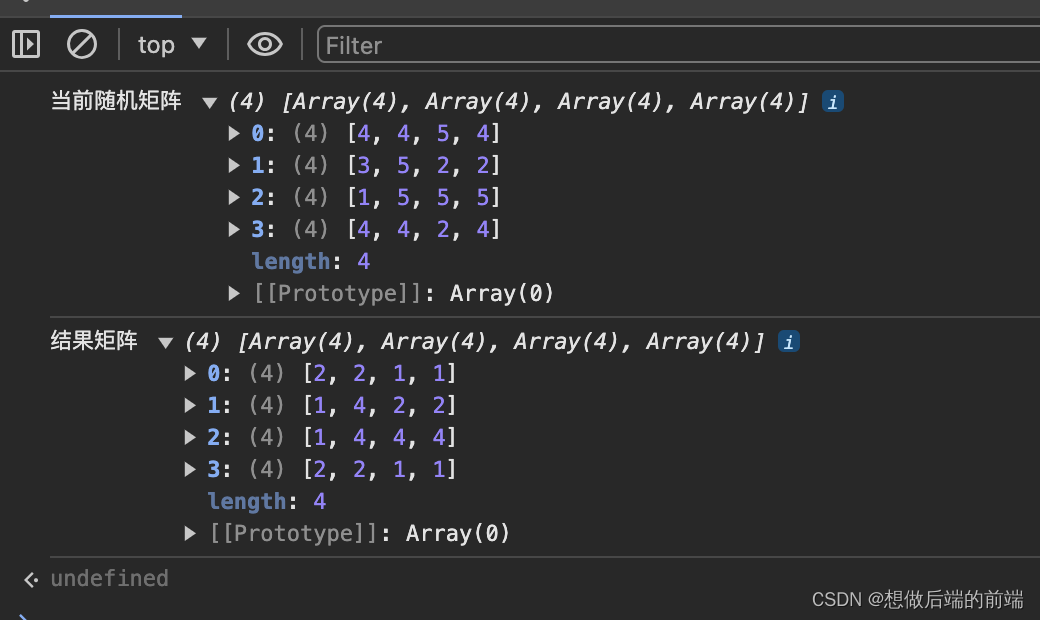
}()console.log("当前随机矩阵",gameMatrix)function detectCount(i,j,cur,path){let key = i+","+j;path.push(key)let inArea = (i,j)=>{return i>=0 && i<4 && j>=0 && j<4; }[[0,1],[0,-1],[1,0],[-1,0]].forEach((dir)=>{let x = i+dir[0];let y = j+dir[1];if(inArea(x,y) && this.gameMatrix[x][y] == cur && !path.includes(x+","+y)){return detectCount(x,y,cur,path)}})return path.length;}function detectAround(){let countMatrix = new Array(4).fill(0).map(()=>new Array(4).fill(0));for (let i = 0; i < 4; i++) {for (let j = 0; j < 4; j++) {countMatrix[i][j] = this.detectCount(i,j,this.gameMatrix[i][j],[]);;}}return countMatrix;
}console.log("结果矩阵",detectAround())看一下结果吧
填充算法
上面我们知道了要消除的元素后,我们就可以把对应位置的元素进行消除,把上方的元素向下滑动然后在空余填充新的元素。概括起来就时以下三种操作,完全可以通过一个算法实现。
- 消除
- 滑动
- 填充
function detectHeight(i,j,isDown){let height = 0;if (isDown) {for (let k = j + 1; k < 4; k++) {if (this.countMatrix[k][i] >= 3) {height++;}}} else {for (let k = 0; k < j; k++) {if (this.countMatrix[k][i] < 3) {height++;}}}return height;
}function fillMatrix(){let help = new Map();for (let i = 0; i < 4; i++) {for (let j = 0; j < 4; j++) {if(this.countMatrix[i][j] < 3){let key = i+","+j;help.set(key,this.gameMatrix[i][j]);}}}for (let i = 0; i < 4; i++) {for (let j = 0; j < 4; j++) {let key = i+","+j;if(help.has(key)){let height = detectHeight(i,j,true);this.gameMatrix[i][j+height] = help.get(key);}else{let height = detectHeight(i,j,false);this.gameMatrix[i][j-height] = 100;}}}}
计算结果:
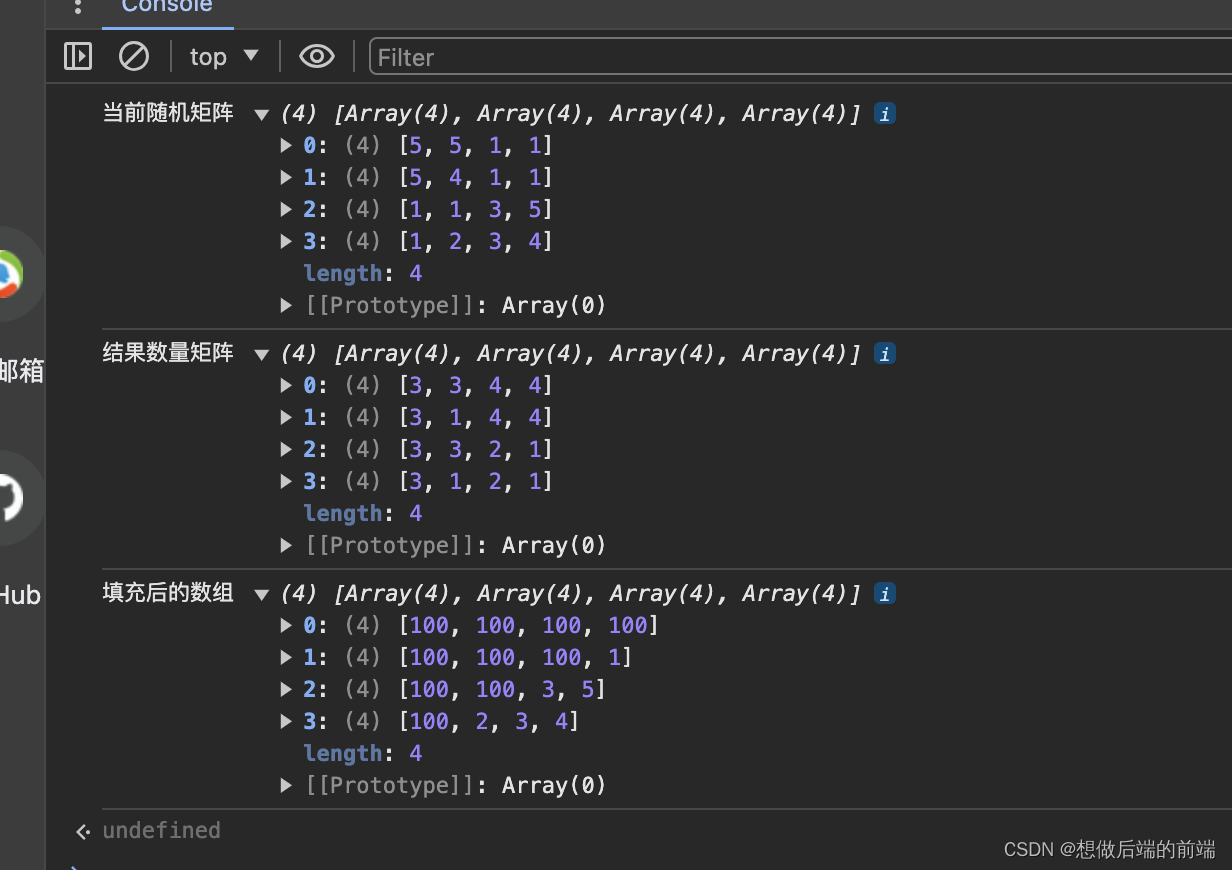
这是我找的比较好的一种结果,这个算法目前还有点问题。等我后续补齐吧。或者谁发现问题了帮我看看。
这篇关于消消乐算法总结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








