34. BI - 美国大学生足球队的 GCN 案例

本文主要是介绍34. BI - 美国大学生足球队的 GCN 案例，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文为 「茶桁的 AI 秘籍 - BI 篇 第 34 篇」

Hi，你好。我是茶桁。

在上一节课中，因为需要，我们先是回顾了一下 Graph Embedding，然后跟大家讲解了 GCN 以及其算法。虽然是推导完了，不过具体要怎么使用可能很多同学还是不太清楚，那咱们这一节课，就拿一个例子来看看具体的 GCN 该怎么去用。

美国大学生足球队 Embedding（GCN）

首先用 networkx 对图做一个处理，原始数据去加载的时候是read_gml:

import networkx as nx
G = nx.read_gml(path + '/LPA/football.gml')

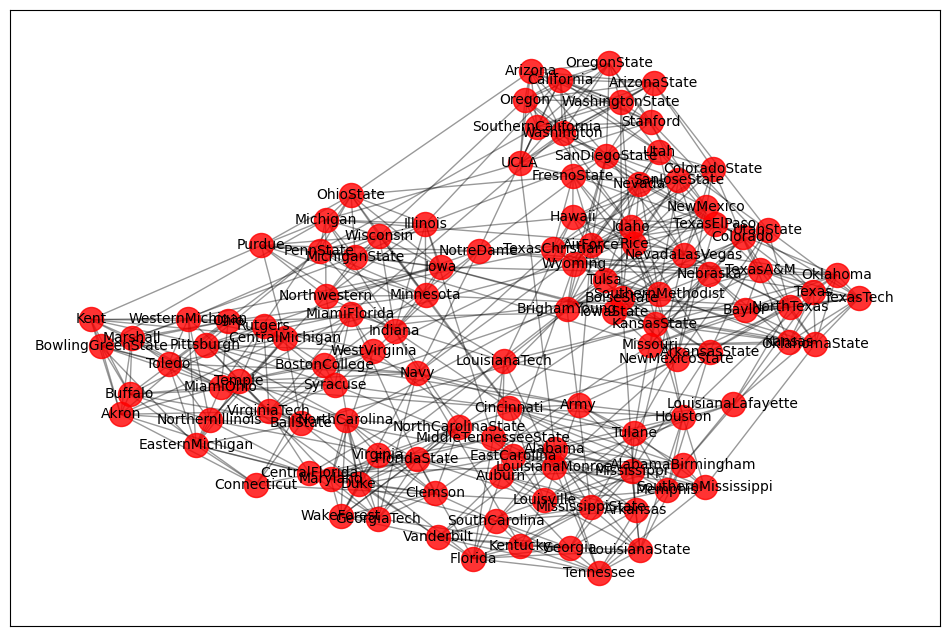
读进来的数据进行可视化，去看一下顶点的情况，看一下某一个数值的取值。

# 可视化
plot_graph(G)
print(list(G.nodes()))
print(G.nodes['BrighamYoung']['value'])---
['BrighamYoung', ..., 'Hawaii']
7

然后先对字母做个排序，排序以后对它求一个邻接矩阵。

# 按照字母顺序排序
order = sorted(list(G.nodes()))
print(order)# 邻接矩阵
A = nx.to_numpy_array(G, nodelist = order)
print(A)---
['AirForce', ..., 'Wyoming']
[[0. 0. 0. ... 0. 0. 1.][0. 0. 0. ... 0. 0. 0.][0. 0. 0. ... 0. 0. 0.]...[0. 0. 0. ... 0. 1. 0.][0. 0. 0. ... 1. 0. 0.][1. 0. 0. ... 0. 0. 0.]]

这个邻接矩阵和图是完全对应的，一个球队有比赛就为 1，没有比赛就为 0。

只是提取邻接特征可能会把自己忘下，所以还要生成一个对角矩阵。

I = np.eye(G.number_of_nodes())
A_hat = A + I
print(A_hat)---
[[1. 0. 0. ... 0. 0. 1.][0. 1. 0. ... 0. 0. 0.][0. 0. 1. ... 0. 0. 0.]...[0. 0. 0. ... 1. 1. 0.][0. 0. 0. ... 1. 1. 0.][1. 0. 0. ... 0. 0. 1.]]

将其写成一个 A_hat 这种形式做一个累加，对角矩阵的对角线都为 1，因为加了一个 I。然后我们想要求一下它的度矩阵 D_hat:

# D_hat 为 A_hat 的度矩阵
D_hat = np.sum(A_hat, axis=0)
print('D_hat: \n', D_hat)---
[[11. ... 12.]]

# 得到对角线上的元素
D_hat = np.matrix(np.diag(D_hat))
print('D_hat: \n', D_hat)---
D_hat: [[11.  0.  0. ...  0.  0.  0.]...[ 0.  0.  0. ...  0.  0. 12.]]

D_hat 本质上一开始得到的是一个向量，这个向量代表含义是你打比赛的次数，就是连接边的个数。一共有115支球队，每个球队打的比赛的次数就放上来了。原来是个向量，现在把它列成对角线，用 np.matrix 进行生成。

前面这些都生成完了，下面就要做一些特征的提取，对 GCN 的算子去进行使用。在特征提取之后，每一层的神经元都有一些连接，咱们把神经元的参数做一个除法。

# 第一层神经元， 4 个维度
W_1 = np.random.normal(loc=0, scale=1, size=(G.number_of_nodes(), 4))# 第二层神经元，4 => 2
W_2 = np.random.normal(loc=0, size=(W_1.shape[1], 2))
print('W_1: \n', W_1)
print('W_2: \n', W_2)---
W_1: [[ 1.79361799e+00  1.00663949e-01  3.15681973e-01  1.57018908e+00]
...[ 3.83597029e-02 -4.11584967e-02  1.23188020e+00  8.01688421e-01]]W_2: [[-0.15407588 -0.34138474][-1.08699826  1.29461044][-0.78768133  0.88276975][-0.31945927  0.72302237]]

在神经网络过程中最开始的参数本质上也是一个随机数。在神经网络最开始的部分后面参数学习是通过梯度下降来进行学习的，但最早期可以采用随机数，这个随机数是 normal 的方法，normal 就是正态分布。我们是在 0 附近做了一个很小的随机数。

有两层神经元 W_1 和 W_2，如果要加非线性特征可以用 relu，来定义一下：

# 当 x<0 时，结果 = 0，x >= 0 时，结果 = x
def relu(x):return (abs(x)+x) / 2

relu 的计算方式就是 x 加上 abs(x)，绝对值，然后再除以2。如果 x 大于 0 它就等于 x，如果小于 0 它就等于 0，这就是 relu 的函数定义。

GCN 这一层的计算逻辑，D_hat 的 -1 次方，其实就是一个倒数的概念。然后乘上 A，A 是邻接矩阵，X 是输入值，W 是权重系数。乘完以后，前面加一层 relu。

这就是 GCN 层的一个提取，同时又加了一个激活函数。现在我来问问大家，这一部分咱们是用了第几种的拉普拉斯算子？其实就是我上一节课中讲的第二种算子，写出来大家回顾一下：

$$\begin{array}{r}{L}^{rw}=D^{-1}A\end{array}$$

实际上逻辑也一样，你也可以用第三种的，都是一样。

把 GCN 层定义下来以后，现在是做了两层的 GCN。最开始的原始数据就输个对角线，第一层的输出结果就是 H_1，把它作为下一层的输入，然后得到了第二层的结果 H_2。H_2 输出就不做其他操作，就把它当成 output 进行输出就可以了。

以上就是 GCN 的一个特征提取，后面咱们一起来看一看，下面其实都是去画一张图，把特征提取的结果通过一种转化的形式给他画一张图，详细的可以去看我上传的源代码。

# 绘制 output，节点 GCN Embedding 可视化
def plot_node(output, title):for i in range(len(nodes)):node_name = nodes[i]value = G.nodes[node_name]['value']plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,label=str(i), color=getValue(value), alpha=0.5, s=250)plt.text(np.array(output)[i,0],np.array(output)[i,1] ,i, horizontalalignment='center',verticalalignment='center', fontdict={'color':'black'})plt.title(title)plt.show()plot_node(output, 'Graph Embedding')

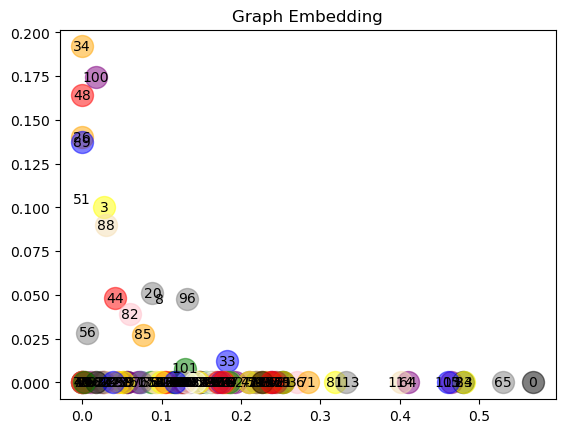
之前的代码中，咱们是做了 relu 这部分的激活函数，其实我还做了一份没有 relu 的代码，一样把它可视化出来：

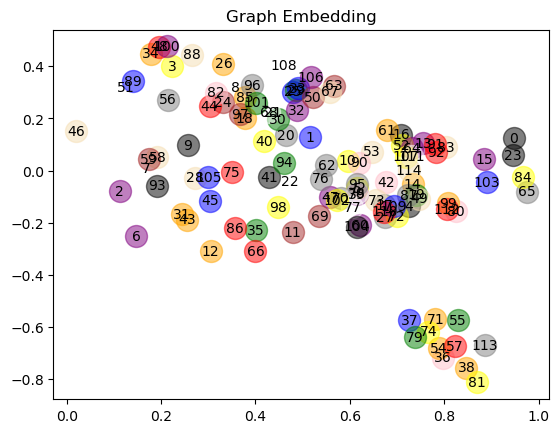
我们来看两种方式，放到二维平面上面，relu 的这个特征提取的好吗？提取得好不好是看后续方不方便做分类任务，如果都挤在一起这个分类就不一定好做了对吧？不带 relu 的特征提取似乎是更理想一些，所以从这个结论上来去看，我们并没有学习，只是用随机数来进行了一个计算。第二，也没有加 relu，GCN的特征提取能力已经很强大了。

所以，其实 GCN 本身的特征提取能力就还不错，而且我们也是拿随机数来进行特征提取，特征提取能力还是比较强大的。以上就把 GCN 的算子用于神经网络的计算，而整个的神经网络就是这样的一套逻辑。

特征的好坏的评价标准是用于后续任务来去做衡量的，如果它分布的比较开那后续可能就比较好计算了。真正写项目的时候要不要加 relu 呢？刚才那个数据集比较简单，也才115支球队，所以不加 relu 是OK的，加了反而效果可能不好。那有些时候还是要试的，有的时候如果数据集比较复杂，加了 relu 效果会更好一点。

GCN 的这套逻辑其实并不是特别复杂，就是在神经网络上面对图做了一个特征提取。它的本质就是提取邻居的特征，再加上自己的特征，方便后续做特征提取的计算，同时又做了一些降维的处理。

那本节课只是拿美国大学生足球队的这个例子初步的来了解一下 GCN 的整个过程和逻辑，之前咱们也用过这个数据，大家可以自行去对比一下。

下一节课，咱们来看一个实际的项目。

这篇关于34. BI - 美国大学生足球队的 GCN 案例的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---