LLama的激活函数SwiGLU 解释

本文主要是介绍LLama的激活函数SwiGLU 解释，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Swish激活函数

1. Swish函数公式

LLaMA模型中的激活函数

1. SwiGLU激活函数

2. SwiGLU激活函数的表达式

3. SwiGLU激活函数的优势

Swish激活函数

Swish是一种激活函数，其计算公式如下：

1. Swish函数公式

Swish(x) = x * sigmoid(x)

其中，sigmoid(x)是sigmoid函数，计算公式为：

sigmoid(x) = 1 / (1 + exp(-x))

Swish函数结合了线性函数和非线性函数的特点，能够自适应地调整激活函数的形状，因此在某些深度学习模型中，Swish函数的表现优于常见的ReLU函数。

LLaMA模型中的激活函数

在LLaMA模型中，使用的激活函数是SwiGLU[1][2][3]。

1. SwiGLU激活函数

SwiGLU是LLaMA模型在前馈神经网络（FFN）阶段使用的激活函数[2:1]。它取代了ReLU非线性函数，以提高模型的性能[3:1]。

2. SwiGLU激活函数的表达式

SwiGLU是Gated Linear Units（GLU）激活函数的一种变体，其公式为：

SwiGLU(x,W, V, b, c) = Swish_1(xW + b) ⊗ (xV + c)

其中，Swish_β(x) = x σ(β x)，σ为sigmoid函数，⊗为逐元素乘[1][2][3]。

3. SwiGLU激活函数的优势

SwiGLU的优势主要体现在以下几个方面：

3.1 提升性能：SwiGLU被应用于Transformer架构中的前馈神经网络（FFN）层，用于增强性能[1:1][2:1][3:1]。

3.2 可微性：SwiGLU是处处可微的非线性函数[1:2]。

3.3 自适应性：GLU是一种类似于长短期记忆网络（LSTM）带有门机制的网络结构，通过门机制控制信息通过的比例，来让模型自适应地选择哪些单词和特征对预测下一个词有帮助[3:2]。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import normdef gelu(x):return x * norm.cdf(x)def relu(x):return np.maximum(0, x)def swish(x, beta=1):return x * (1 / (1 + np.exp(-beta * x)))def swiglu(x, W, V, b, c):return swish(x*W + b) * (x*V + c)x_values = np.linspace(-5, 5, 500)
gelu_values = gelu(x_values)
relu_values = relu(x_values)
swish_values = swish(x_values)
swish_values2 = swish(x_values, beta=0.5)
swiglu_values = swiglu(x_values, 1, 1, 0, 0) # Here you need to set the parameters W, V, b, and c according to your needsplt.plot(x_values, gelu_values, label='GELU')
plt.plot(x_values, relu_values, label='ReLU')
plt.plot(x_values, swish_values, label='Swish')
plt.plot(x_values, swish_values2, label='Swish (beta=0.5)')
plt.plot(x_values, swiglu_values, label='SwiGLU')
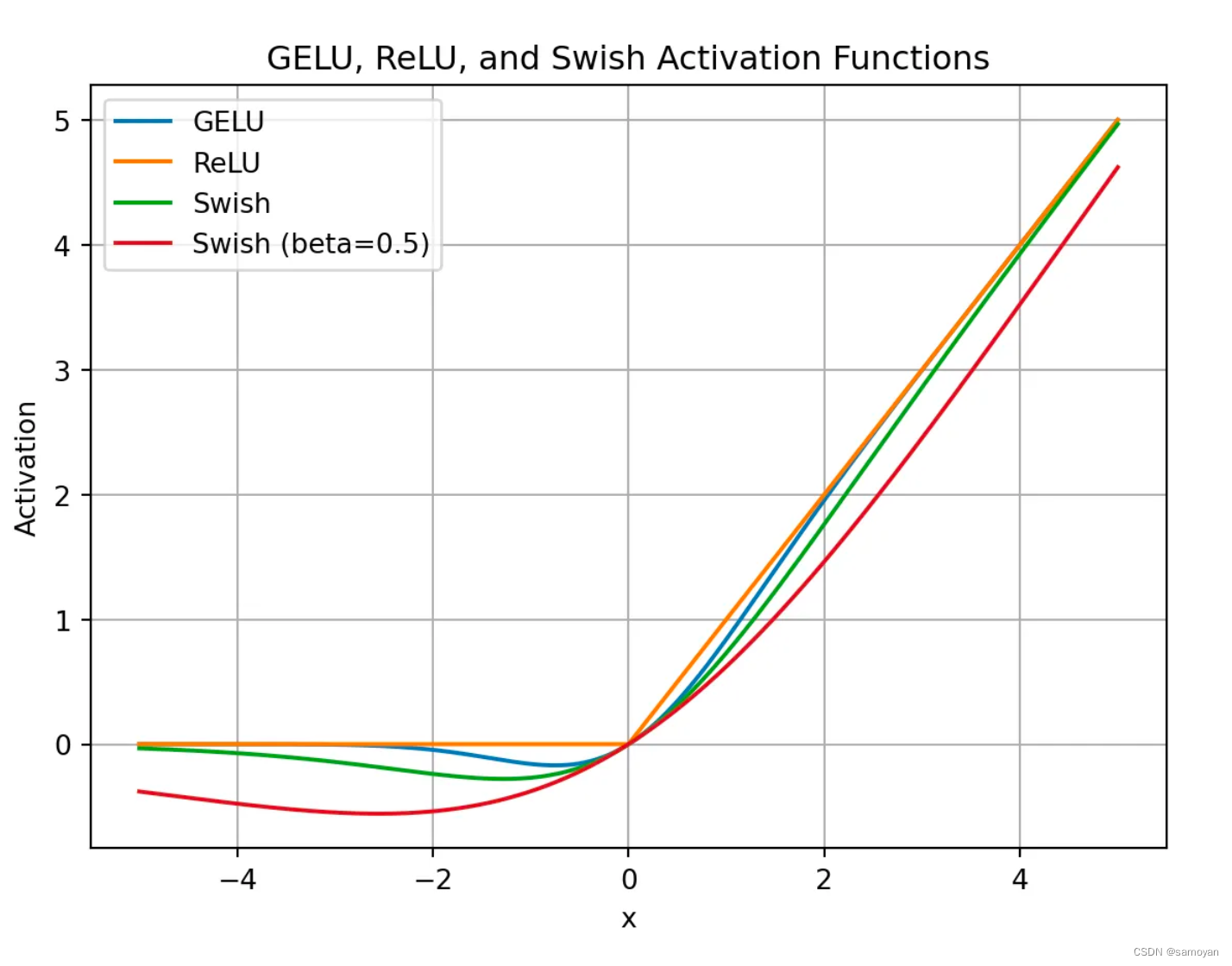
plt.title("GELU, ReLU, Swish, and SwiGLU Activation Functions")
plt.xlabel("x")
plt.ylabel("Activation")
plt.grid()
plt.legend()
plt.show()