【随想录】Day30—第七章回溯算法part06

本文主要是介绍【随想录】Day30—第七章回溯算法part06，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目1: 重新安排行程

题目链接：332. 重新安排行程

1- 思路

思路：

本题实际上是一个搜索的过程，即搜索满足输入条件从起点到一个终点可达的路径，同时路径要满足字典序小的排在前面。因此需要借助一个数据结构，实现存储当前机场可达到的目的地机场，且存储可以达到的次数，即机票数。
本题以输入：[[“JFK”, “KUL”], [“JFK”, “NRT”], [“NRT”, “JFK”]为例，抽象为树形结构如下：

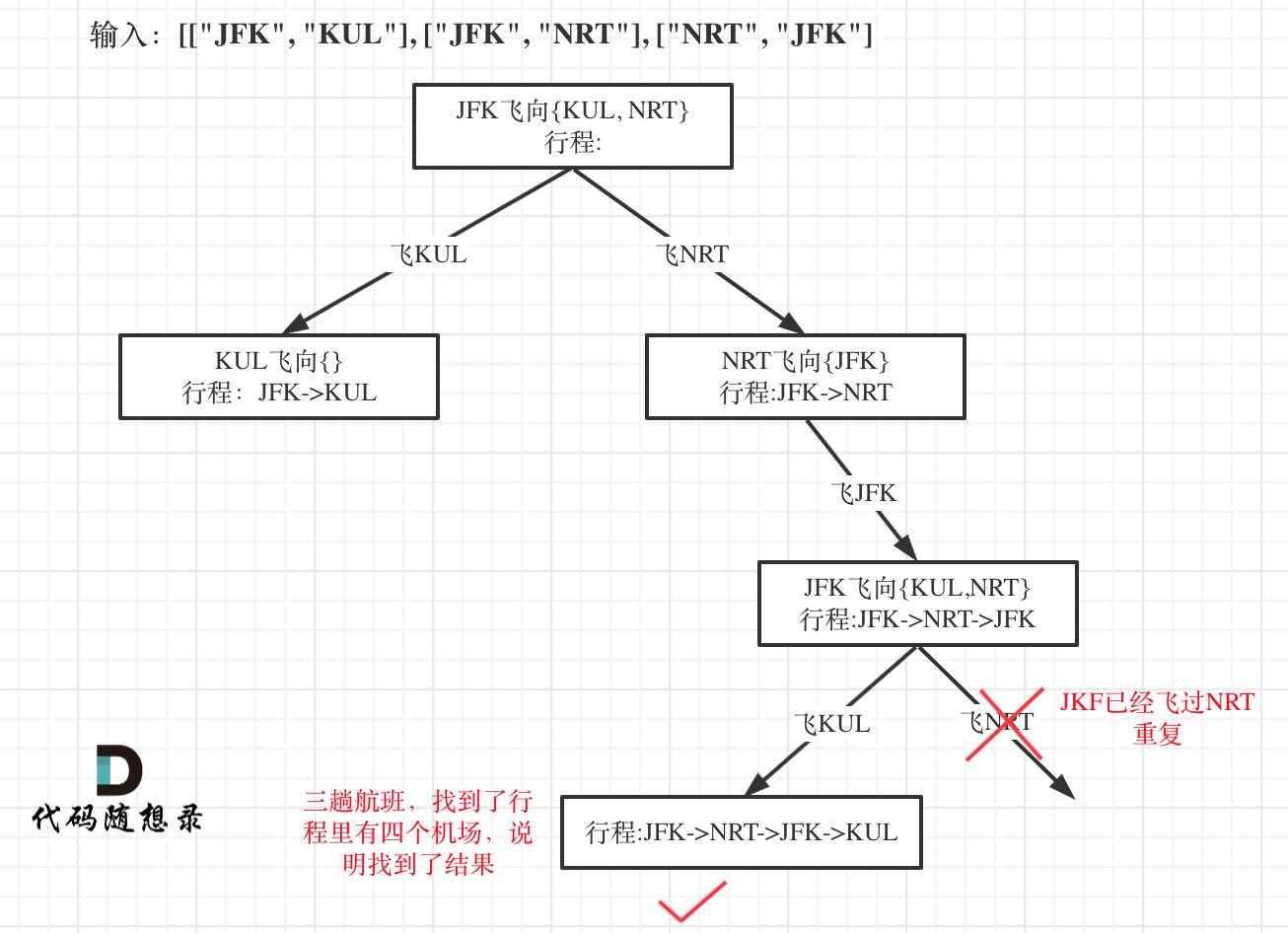
引用carl：代码随想录

根据上述思路使用以下数据结构
数据结构：

定义一个 HashMap 结构为 <String,Map<String,Integer>>：其中Map的第一个 String 存储的是出发点，第二个 String 存储的为目的地，Integer 存储的是从出发点到目的地的机票数。
List<String> res：收集最终的路线结果集

回溯三部曲

1. 回溯函数参数及返回值
本题主要通过将输入的 List<List> 存入 map 中，通过定义全局变量 map 的形式来进行回溯，因此回溯参数传入的是 ticketNum 即机票数量。
函数返回值是 boolean
因为我们只需要找到一个行程，就是在树形结构中唯一的一条通向叶子节点的路线，如图：

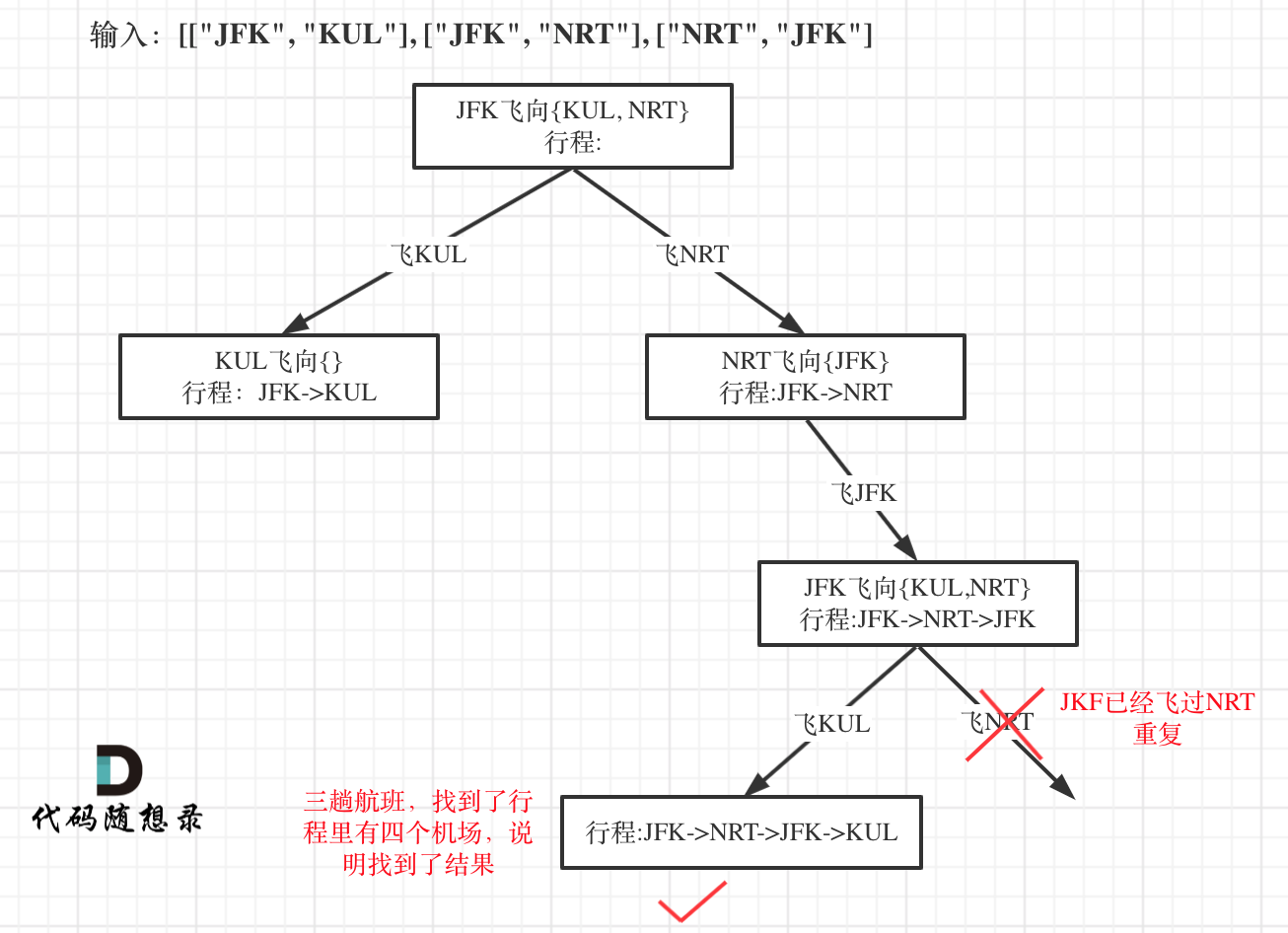
所以找到了这个叶子节点了直接返回。

private boolean BackTracing(int ticketNum)

其中 res 和 map 需要初始化
- 定义 Map<String,Integer> temp ，用于对当前出发点的 目的地 及 机票数 进行操作。
- 如果当前出发点存在，则获取当前出发点，将现有目的地存入，或 +1
- 如果当前出发点不存在，则利用 TreeMap的特性，保证 temp 中的目的地顺序是升序

for(List<String> t : tickets) {Map<String,Integer> temp;// 如果在if(map.containsKey(t.get(0))){temp = map.get(t.get(0));temp.put(t.get(1),temp.getOrDefault(t.get(1),0)+1);}else{// 不存在temp = new TreeMap();temp.put(t.get(1),1);}map.put(t.get(0),temp);
}
res.add("JFK");

**2. 回溯终止条件 **
因为 res 记录的是结果集，而 ticketNum 记录的是路径数，路径比节点数少 1 ，因此终止条件是 res.size() == ticketNum+1

// 3.2 终止条件
if(res.size() == ticketNum+1){return true;
}

3. 回溯逻辑
获取 res 中的最后一个元素，通过 forEach 循环来遍历 key 为最后一个元素的结果集
count为机票数，若机票数 count > 0 则进行递归和回溯
- res 收集当前目的地
- target 列表记录数减 1
- 递归
- 回溯 res
- 回溯 target

if(map.containsKey(last)){// 遍历 mapfor(Map.Entry<String,Integer> target : map.get(last).entrySet()){int count = target.getValue();if(count>0){res.add(target.getKey());target.setValue(count-1);if(BackTracing(ticketNum)) return true;res.removeLast();target.setValue(count);}}}

2- 题解

⭐重新安排行程 ——题解思路

在这里插入图片描述

class Solution {List<String> res = new ArrayList<>();Map<String,Map<String,Integer>> map = new HashMap<>();public List<String> findItinerary(List<List<String>> tickets) {// 初始化for(List<String> t :tickets){Map<String,Integer> tmp;// 如果存在if(map.containsKey(t.get(0))){tmp = map.get(t.get(0));tmp.put(t.get(1),tmp.getOrDefault(t.get(1),0)+1);}else{tmp = new TreeMap();tmp.put(t.get(1),1);}map.put(t.get(0),tmp);}res.add("JFK");backTracing(tickets.size());return res;}// 回溯public boolean backTracing(int tNum){if(res.size() == tNum+1){return true;}// 回溯String last = res.getLast();// 如果有if(map.containsKey(last)){// 遍历 mapfor(Map.Entry<String,Integer> target : map.get(last).entrySet()){// 递归 && 回溯int count = target.getValue();if(count>0){res.add(target.getKey());target.setValue(count-1);if(backTracing(tNum)) return true;res.removeLast();target.setValue(count);}}}return false;}
}

题目2: N皇后

题目链接：N 皇后

1- 思路

题目所求，在 n*n 的棋盘中方 n 个皇后，且 n 皇后满足不存在 _**同行、同列、同对角 **_的元素。

递归树

递归树每层的结果实际上是每层皇后的所取的位置

思路：

1. 数据结构
- List<List<String>> res：收集结果
2. 回溯三部曲
- 2.1 回溯参数及返回值
  - int n：棋盘大小
  - int row：回溯到第几行
  - char[][] cheesboard：棋盘数组
- 2.2 回溯终止条件 && 结果收集
  - 如果 row 遍历到了 n 的大小，则证明已经求出一个解，此时直接收集结果
- 2.3 回溯逻辑
  - 如果当前遍历的位置 符合(isValid) 结果则进行递归+回溯
  - 对 cheesboard[row][i] 进行放棋子
  - 递归 backTracing(n,i+1,cheesboard)
  - 回溯 cheesboard[row][i]
3. 实现 isValid 函数判断是否有效
- 行判断
- 列判断
- 左上判断
- 右上判断
4. 实现 Array2List 函数，收集 char 数组的结果

    public List Array2List(char[][] cheesboard){List<String> list = new ArrayList<>();for(char[] c:cheesboard){list.add(String.copyValueOf(c));}return list;}

2- 题解

⭐N皇后 ——题解思路

在这里插入图片描述

class Solution {List<List<String>> res = new ArrayList<>();public List<List<String>> solveNQueens(int n) {// 定义 cheesboard 并初始化char[][] cheesboard = new char[n][n];for(char[] c:cheesboard){Arrays.fill(c,'.');}backTracing(n,0,cheesboard);return res;}public void backTracing(int n,int row,char[][] cheesboard){// 终止if(row == n){res.add(Array2List(cheesboard));return ;}// 回溯for(int i = 0 ; i < n;i++){if(isValid(row,i,n,cheesboard)){cheesboard[row][i] = 'Q';backTracing(n,row+1,cheesboard);cheesboard[row][i] = '.';}}}public List Array2List(char[][] cheesboard){List<String> list = new ArrayList<>();for(char[] c:cheesboard){list.add(String.copyValueOf(c));}return list;}public boolean isValid(int row,int col,int n,char[][] cheesboard){// 列for(int i = 0;i<row;i++){if(cheesboard[i][col] =='Q' ){return false;}}// 行for(int i = 0;i<col;i++){if(cheesboard[row][i] =='Q' ){return false;}}// 45for(int i =row-1,j = col-1; i>=0 && j>=0 ;i--,j--){if(cheesboard[i][j]=='Q'){return false;}}for(int i =row-1,j = col+1; i>=0 && j<=n-1 ;i--,j++){if(cheesboard[i][j]=='Q'){return false;}}return true;}
}