本文主要是介绍OFDM-OCDM雷达通信一体化信号模糊函数对比研究【附MATLAB代码】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章来源:微信公众号:EW Frontier
1.引言
为提高频谱利用率并实现系统小型化、集成化,近年来雷达通信一体化系统成为重要研究方向。正交线性调频波分复用(OCDM)信号是利用菲涅尔变换形成的一组正交线性啁啾(chirp)信号,基于OCDM 的雷达通信一体化信号不仅具有正交频分复用(OFDM)信号的频谱利用率高、适合高速数据传输等优点,且具有更好的抗多径干扰能力,被认为是较好的OFDM 一体化信号替代方案[1]。
本文主要通过对比分析OCDM与OFDM模糊函数,说明二者各自优缺点,为下一步雷达通信一体化研究提供参考。
2.正交线性调频波分复用
正交线性调频波分复用(Orthogonal Chirp Division Multiplexing,OCDM)是一种基于离散菲涅尔变换(Discrete Fresnel Transform,DFnT)的多载波正交复用技术,因其在多径传播中具有更好的鲁棒特性,被认为是正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM) 技术[1] 的替代方案。
2.1 OCDM信号
OCDM 信号由Ouyang[2] 于2016 年首次提出,由一组在时域与频域上重叠的啁啾(chirp)信号组成,且每一个啁啾信号在啁啾维度相互正交,在传输时不会互相干扰。第k 个啁啾信号可由下式表示:
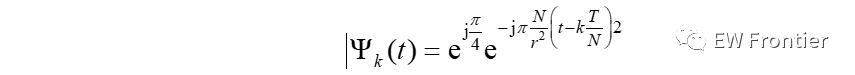
添加图片注释,不超过 140 字(可选)
式中N 为啁啾信号的个数,T 为OCDM 信号的周期。利用每个啁啾信号的幅度加载通信信息可构成OCDM 一体化信号。本文将调制在第m 个符号的第k 个啁啾上的随机通信信息设为xm(k),则离散化的一体化OCDM 信号的第m 个符号表示为:
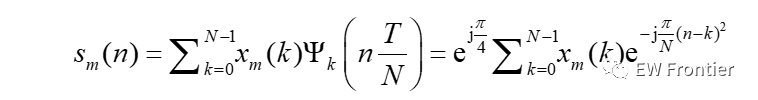
2.2 OCDM一体化系统
OCDM的基本原理是通过在相同带宽中利用菲涅尔变换形成一组正交的线性Chirp 信号,并将通信信息加载到这一组Chirp信号的幅度和相位中,从而实现高效通信数据传输[2]。
菲涅尔变换在OCDM信号形成中的作用类似于傅里叶变换在OFDM信号形成中的 作用,利用离散菲涅尔变换(DFnT)实现OCDM的数字实现,在发射端利用离散菲涅 尔逆变换(IDFnT)生成OCDM信号,利用DFnT在接收端恢复OCDM信号。通过利用每个Chirp信号的幅度和相位传输通信信息,构成OCDM一体化信号。若采用16QAM进行数据传输,则得到如下OCDM一体化系统[3-4]:
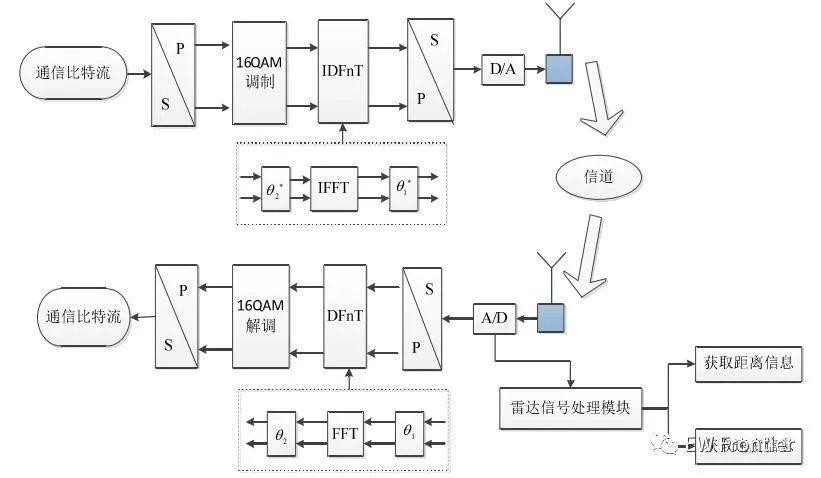
图1 OCDM一体化系统的实现框图
实现的具体步骤如下[3-4]:
第一步,在发射端将串行通信比特流通过16QAM调制后,串并转换,形成通信符号x;
第二步,将并行的通信符号,与以二次相位项的共轭为对角线数据的矩阵相乘;
第三步,将第二步所得矩阵进行IFFT变换后,与以二次相位项的共轭为对角线 数据的矩阵相乘形成OCDM一体化信号,并将其进行并串转换,通过数模转换器和混 频器发送;
第四步,在接收端将接收到的信号通过混频器和模数转换器,生成数字信号,一方 面将其发送给雷达信号处理模块,进行目标速度和距离的求取。另一方面,将其进行串 并转换,发送给通信信号解调模块;
第五步,将并行信号与以二次相位项1为对角线数据的矩阵相乘,再通过FFT变 换后,与以二次相位项2为对角线数据的矩阵相乘,从而获得通信符号数;
第六步,将通信符号进行16QAM解调,获得通信信息。
3.OFDM-OCDM仿真分析
为方便分析二者模糊函数差异,本文简化对比,不加入调制信息,同时默认为单符号,其余参数设置如下:子载波数:16;脉冲时间:1us;调频斜率:16000GHz/s。

图2 OFDM模糊函数
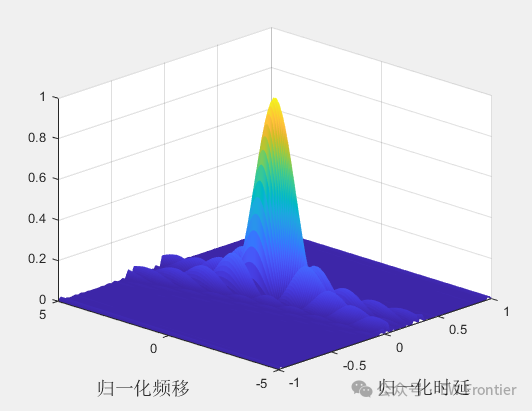
图3 OCDM模糊函数
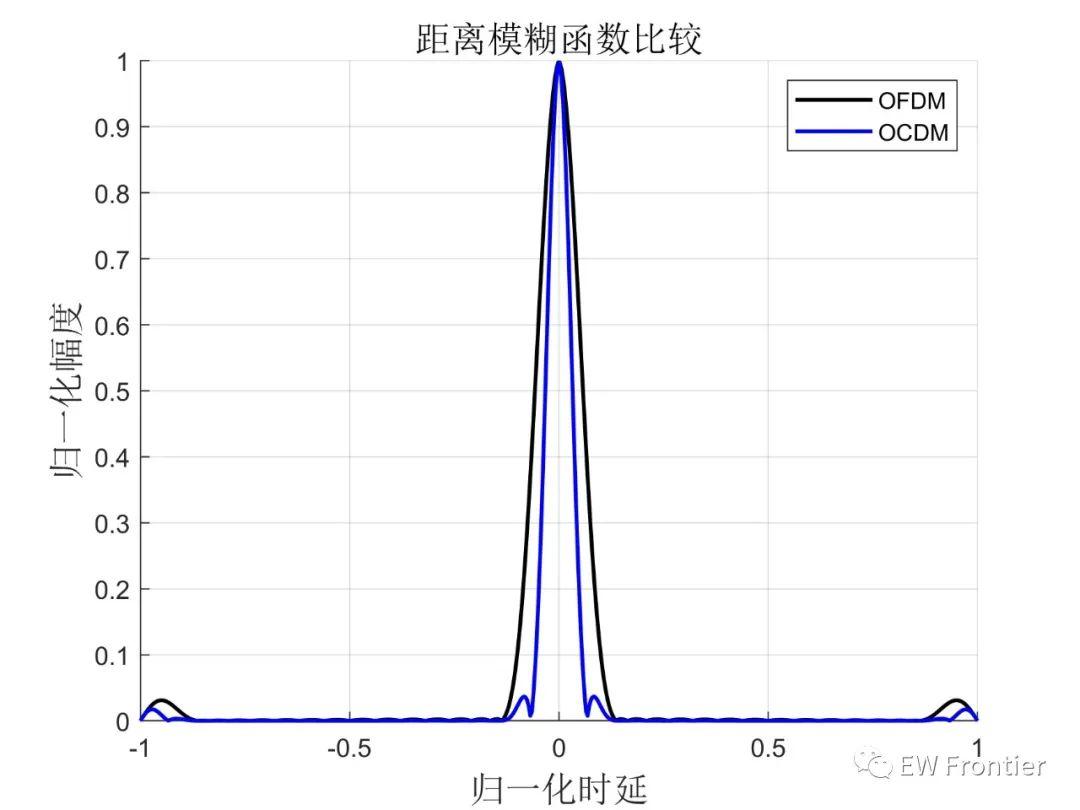
图4 OCDM与OFDM距离模糊函数
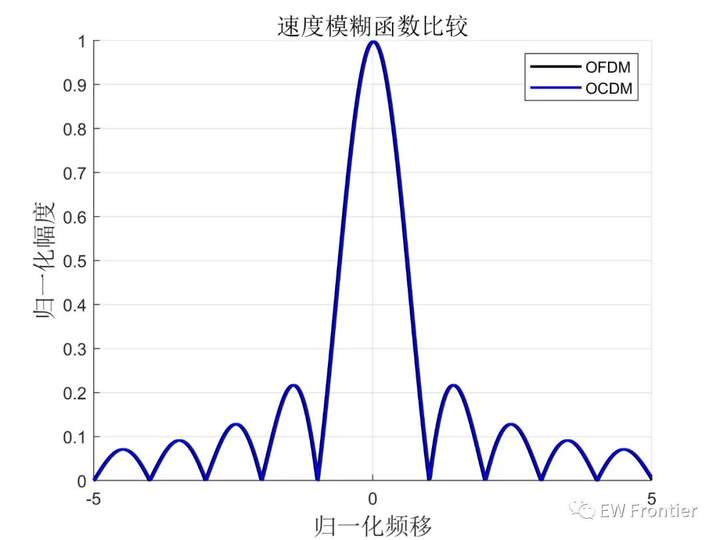
图5 OCDM与OFDM速度模糊函数
从图2至图5,可以发现 OCDM 模糊图形状近似图钉型,中心峰值窄,具有良好距离分辨力和速度分辨力,同时能量在速度距离平面的分布除中心峰值外较为平坦说明不易产生模糊, 旁瓣较小不易受干扰。相比 OFDM 信号,OCDM 信号零多普勒平面的主瓣宽度更窄, 旁瓣更低,具有更好的距离分辨特性,两者的零时延平面模糊图差异不大。
总结
本文主要基于传统OFDM雷达通信一体化信号体制,将OFDM的替代技术OCDM引入,介绍了OCDM的信号组成结构,OCDM一体化信号系统组成,同时通过仿真分析OCDM与OFDM的模糊函数,进一步说明了OCDM的良好性能,更适合进行雷达探测,为此可以提出更优秀的雷达通信一体化信号,将16QAM、BPSK、MSK等调制技术与OCDM相结合,希望对研究雷达通信一体化的小伙伴有帮助。
参考文献
[1]王晶琦,曾欢,陶詹等.一种基于OCDM的新型雷达通信一体化系统[J].微波学报,2022,38(06):14-18.DOI:10.14183/j.cnki.1005-6122.202206004.
[2]Ouyang X, Zhao J. Orthogonal chirp divisionmultiplexing for coherent optical fiber communications[J]. Journal of LightwaveTechnology, 2016, 34(18): 4376-4386
[3]吕鑫. OCDM-OFDM雷达通信一体化信号设计与研究[D].南京理工大学,2019.DOI:10.27241/d.cnki.gnjgu.2019.000444.
[4]许奥. 基于OCDM的雷达通信一体化技术研究[D].南京理工大学,2021.DOI:10.27241/d.cnki.gnjgu.2021.001034.
MATLAB代码示例
%% OCDM与OFDM的模糊函数比较
%% 全部代码获取 学术交流Q群:479772742
clear all;close all;clc
% 子载波数
N_c=16;
% 脉冲持续时间
T_b=1e-6;
% 归一化时间
x=linspace(-1,1,32*N_c);%-1:0.001:1;
% 归一化频率
y=-5:0.01:5;
% 调频率
mu=16/T_b^2;
% 符号权重
% w=ones(N_c,1);
w=chebwin(N_c,50);
%% 模糊函数
[X,Y]=meshgrid(x,y);
[amf,amt]=size(X);
AF_ofdm = AFmean_single_symbol( N_c,T_b,x,y,w);
AF_ocdm = AFmean_lfm_OFDM_single( N_c,T_b,mu,x,y,w );
figure;grid on;hold on
surf(X,Y,AF_ofdm,'EdgeColor','none')
% title('OFDM平均模糊函数','fontsize',14)
xlabel('归一化时延','fontsize',14),ylabel('归一化频移','fontsize',14)
colormap('default')
% surface(x, [0,0], [zeros(1,amt)
;AF_ocdm(
1
,:)],
'EdgeColor'
,[
000
],
'FaceColor'
,[
000
]);
zlim([0,1]);
view(-46,26)
figure;grid on;hold on
surf(X,Y,AF_ocdm,'EdgeColor','none')
% title('OFDM平均模糊函数','fontsize',14)
xlabel('归一化时延','fontsize',14),ylabel('归一化频移','fontsize',14)
colormap('default')
% surface(x, [0,0], [zeros(1,amt)
;AF_ocdm(
1
,:)],
'EdgeColor'
,[
000
],
'FaceColor'
,[
000
]);
zlim([0,1]);
view(-46,26)
% view(0,90)
%% 距离模糊函数
AC_ofdm=AF_ofdm(501,:);
AC_ocdm=AF_ocdm(501,:);
figure;grid on;hold on;
plot(x,AC_ofdm,'k','linewidth',1.5)
plot(x,AC_ocdm,'b','linewidth',1.5)
title('距离模糊函数比较','fontsize',14);
xlabel('归一化时延','fontsize',14),ylabel('归一化幅度','fontsize',14)
legend('OFDM','OCDM')
% ylim([0,1]);
% xlim([-0.2,0.2])
%% 速度模糊函数
DC_ofdm=AF_ofdm(:,256);
DC_ocdm=AF_ocdm(:,256);
figure;grid on;hold on;
plot(y,DC_ofdm,'k','linewidth',1.5)
plot(y,DC_ocdm,'b','linewidth',1.5)
title('速度模糊函数比较','fontsize',14);
xlabel('归一化频移','fontsize',14),ylabel('归一化幅度','fontsize',14)
legend('OFDM','OCDM')
% xlim([y(1),y(end)]);
% xlim([-5,5])
这篇关于OFDM-OCDM雷达通信一体化信号模糊函数对比研究【附MATLAB代码】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






