【智能算法】回溯搜索算法（BSA）原理及实现

本文主要是介绍【智能算法】回溯搜索算法（BSA）原理及实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

1.背景

2013年，P Civicioglu等人受到当前种群与历史种群之间的差分向量的引导启发，提出了回溯搜索算法（Backtracking Search Algorithm, BSA）。

2.算法原理

2.1算法思想

BSA通过当前种群与历史种群之间的差分向量的引导来执行搜索任务，主要分为三部分：筛选-I、交叉和变异和筛选-II。

2.2算法过程

筛选-I

更新历史种群 Xoldt ，分为以下两步：
$${\mathbf{X}}_{\mathrm{old}}^t=\{\begin{array}{llc}{\mathbf{X}}^t,& \mathrm{if}\phi >\theta & \\ {\mathbf{X}}_{\mathrm{old}}^t,& \mathrm{otherwise}& \end{array}\text{\hspace{1em}(1)}$$
其中，$\phi ,\theta$为随机数。接下来：
$${\mathbf{X}}_{\mathrm{old}}^t=\mathrm{permuting}\left({\mathbf{X}}_{\mathrm{old}}^t\right)\text{\hspace{1em}(2)}$$
permuting 是一个随机改组函数，使得历史种群 Xold t 中包含的 N 个个体随机排序。

交叉和变异

变异操作由历史种群 Xold t 引导：
$${\mathbf{z}}_i^t={\mathbf{x}}_i^t+F\times \left({\mathbf{x}}_{\mathrm{old},i}^t-{\mathbf{x}}_i^t\right)\text{\hspace{1em}(3)}$$
F 为缩放因子，表述为：
$$F=3\times \xi \text{\hspace{1em}(4)}$$
交叉操作是由一个 N 行 D 列的二进制矩阵 M 来引导：
$$x_{i,j}^{t+1}=\{\begin{array}{l}{x}_{i,j}^t,\mathrm{if}{\mathbf{M}}_{i,j}=1\\ z_{i,j}^t,\mathrm{if}{\mathbf{M}}_{i,j}=0\end{array}\text{\hspace{1em}(5)}$$

筛选-II

为了加快收敛过程，执行：
$${\mathbf{x}}_i^{t+1}=\{\begin{array}{llc}{\mathbf{x}}_i^t,& \mathrm{if}f({\mathbf{x}}_i^t)<f({\mathbf{x}}_i^{t+1})& \\ {\mathbf{x}}_i^{t+1},& \mathrm{otherwise}& \end{array}\text{\hspace{1em}(6)}$$

伪代码

3.结果展示

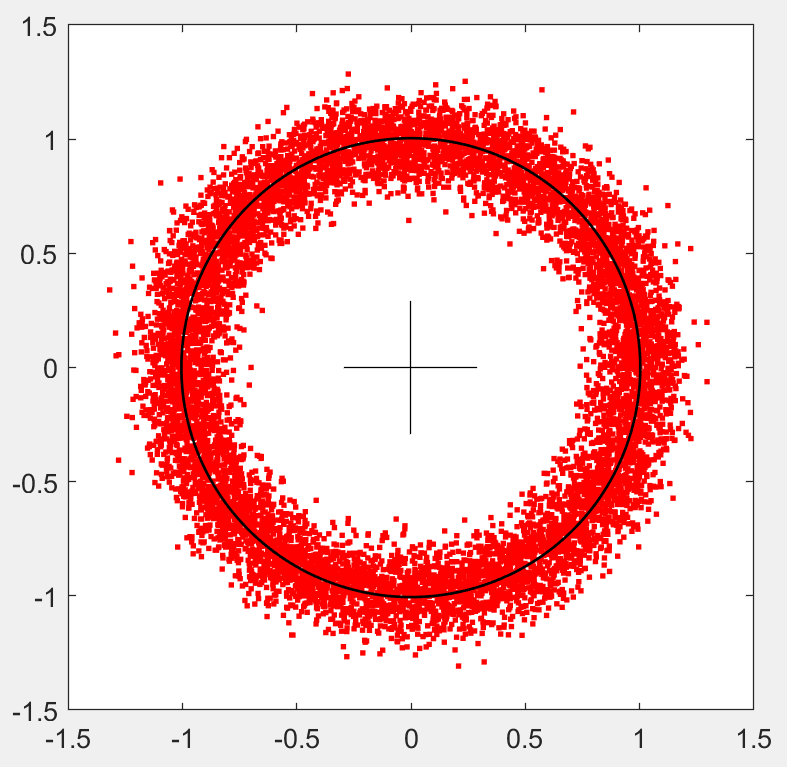
作者提供了拟合圆、图像聚类两个案例：

4.参考文献

[1] Civicioglu P. Backtracking search optimization algorithm for numerical optimization problems[J]. Applied Mathematics and computation, 2013, 219(15): 8121-8144.

这篇关于【智能算法】回溯搜索算法（BSA）原理及实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---