【算法刷题】手撕LRU算法（原理、图解、核心思想）

2024-04-23 05:44
文章标签 算法 原理 图解 刷题 lru 核心思想

本文主要是介绍【算法刷题】手撕LRU算法（原理、图解、核心思想），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

文章目录

  • 1.LRU算法
    • 1.1相关概念
    • 1.2图解举例
    • 1.3基于HashMap和双向链表实现
      • 1.3.1核心思想
      • 1.3.2代码解读
      • 1.3.3全部代码

1.LRU算法

1.1相关概念

  • LRU（Least Recently Used，最近最久未使用算法）：
    • 定义：根据页面调入内存后的使用情况来做决策。LRU页面置换算法选择最近最久未使用的页面予以淘汰；
    • 支持：该算法赋予每个页面一个访问字段，用来记录一个页面自上次被访问内以来锁经历的时间t；当淘汰一个页面时，选择现有页面中 t值最大的（即最近最久未使用的）页面进行淘汰
  • 两种硬件支持（选择其中一种即可）：
    1. 寄存器：
      • 作用：其中包含了标记位和时间戳，标记位可以快速判断缓存块（页面）是否有效，而无需遍历整个栈来查找。时间戳可以快速记录和更新缓存块（页面）的访问时间，而不必每次访问都遍历栈来更新。
    2. 栈：
      • 作用：用于记录缓存块（页面）的访问顺序（当前使用中的各个页面的页面号）。
      • 新增页面步骤：
        • 每当进程访问某页面时，判断该页面在栈中是否存在
          • 若存在，则将该页面的页面号从栈中取出，并将该原页面号压入栈顶；
          • 若不存在，则将栈底元素移除，并将新页面号压入栈顶；
        • 因此，栈顶始终是最新被访问页面的页面号 ， 栈底则是最近最久未使用页面的页面号！

1.2图解举例

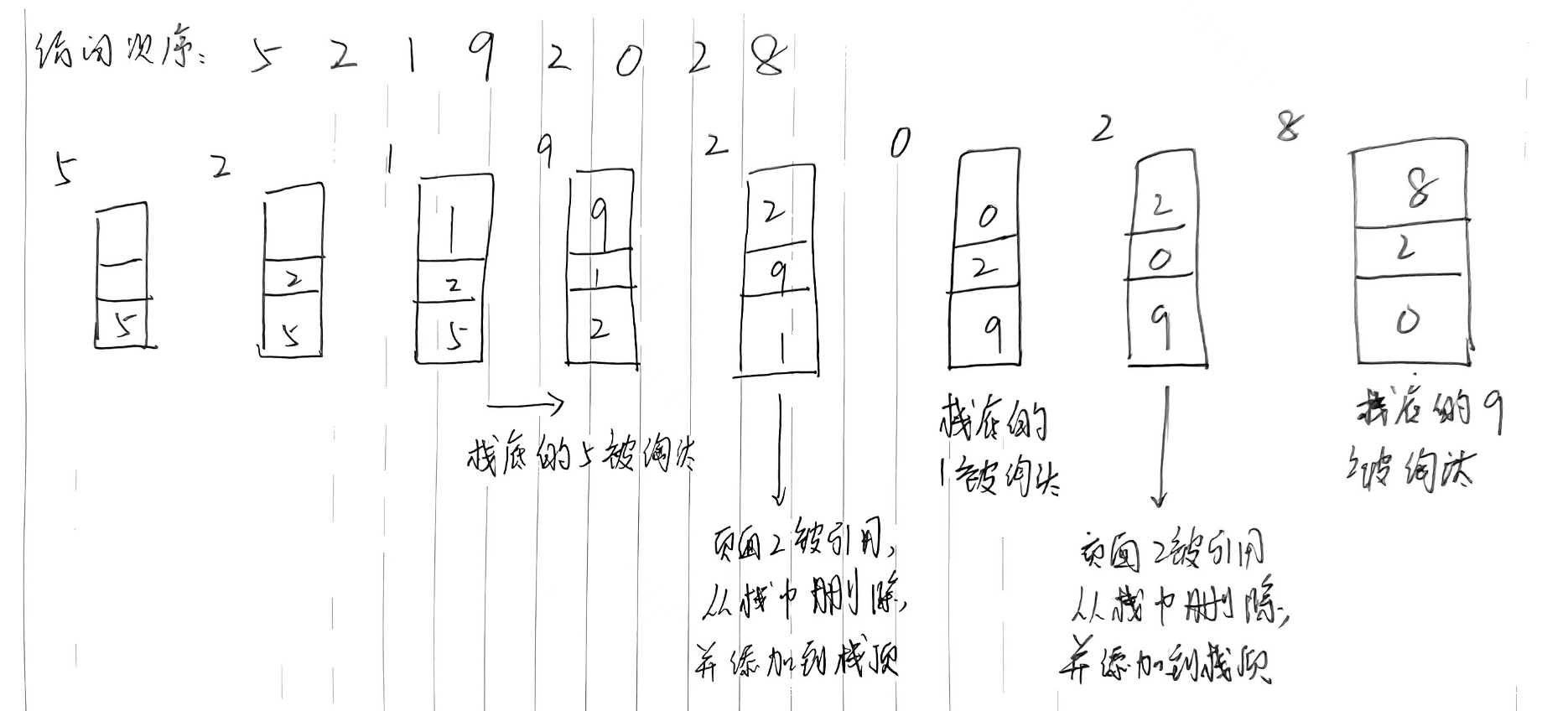
  • 举例前提：假设内存只能容纳3个页大小，进程按照 5 2 1 9 2 0 2 8的次序访问页
  • 假设内存按照栈的方式来描述访问时间，并保证 栈顶始终是最新被访问页面的页面号 ， 栈底则是最近最久未使用页面的页面号

image-20240419170652555

1.3基于HashMap和双向链表实现

1.3.1核心思想

  • 核心思想：使用自定义节点DLinkedNode模拟双向链表，并通过双向链表实现栈功能；

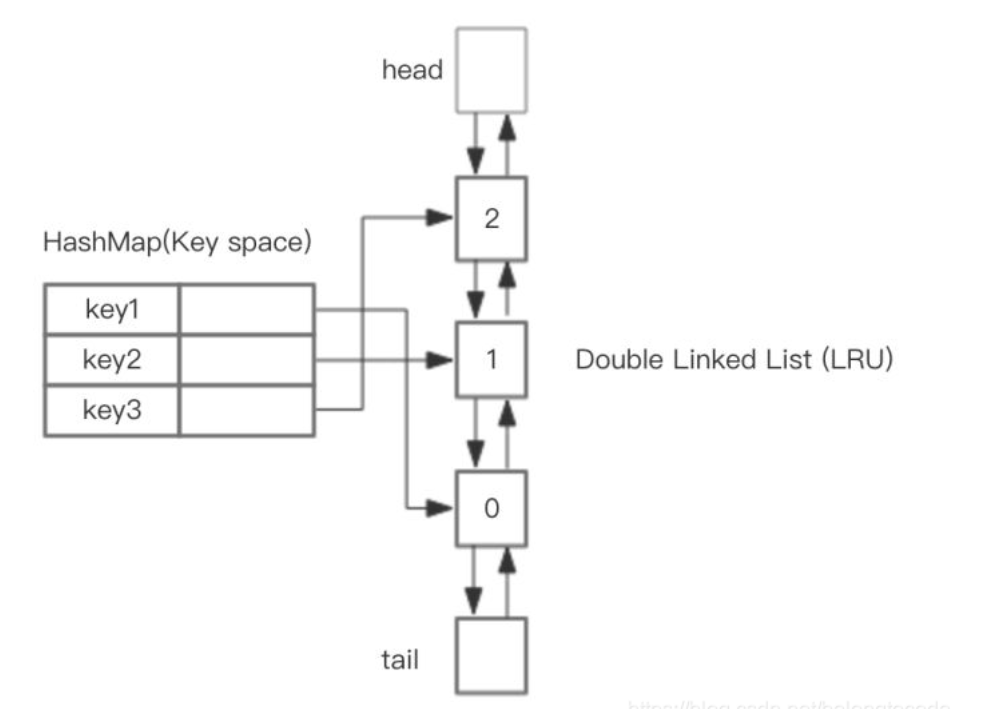
  • 使用HashMap存储以页面号为key，value存储指向双向链表节点的指针

  • 双向链表维护了页面的访问顺序，链表的头部（即栈顶）为最新访问的页面，底部为最久未使用的页面

  • put(key,value)：首先在 HashMap 找到 Key 对应的节点，

    • 如果节点存在，更新节点的值，并把这个节点移动栈顶。
    • 如果不存在，需要构造新的节点，并且尝试把节点塞到栈顶 ，如果LRU空间不足，则通过 tail 淘汰掉栈底的节点，同时在 HashMap 中移除 Key。

image-20240419175738628

1.3.2代码解读

  • DLinkedNode
class DLinkedNode {String key;int value;DLinkedNode pre;DLinkedNode next;
}
  • cache：使用HashTable代替HashMap，线程安全
private Hashtable<String, DLinkedNode> cache = new Hashtable<>();
  • put流程：
public void put(String key, int value) {DLinkedNode node = cache.get(key);if(node == null){DLinkedNode newNode = new DLinkedNode();newNode.key = key;newNode.value = value;this.cache.put(key, newNode);this.addNode(newNode);++count;if(count > capacity){// 淘汰栈底元素DLinkedNode tail = this.popTail();this.cache.remove(tail.key);--count;}}else{//该元素已经存在//将该元素移动到栈顶node.value = value;this.moveToHead(node);}
}
  • 移动栈中的元素到栈顶：
    • 首先先删除该节点 （解除引用）
    • 再添加该节点到栈顶
//将该节点移动到头节点
private void moveToHead(DLinkedNode node){this.removeNode(node);this.addNode(node);
}

//删除该节点（跳过该节点）
private void removeNode(DLinkedNode node){DLinkedNode pre = node.pre;DLinkedNode next = node.next;pre.next = next;next.pre = pre;
}

//添加节点到栈顶
private void addNode(DLinkedNode node){node.pre = head;node.next = head.next;head.next.pre = node;	//头部节点的上一个节点为新节点head.next = node;
}

1.3.3全部代码

class DLinkedNode {String key;int value;DLinkedNode pre;DLinkedNode next;
}public class LRUCache {private Hashtable<String, DLinkedNode> cache = new Hashtable<>();private int count;private int capacity;private DLinkedNode head, tail;public LRUCache(int capacity) {this.count = 0;this.capacity = capacity;head = new DLinkedNode();head.pre = null;tail = new DLinkedNode();tail.next = null;head.next = tail;tail.pre = head;}public void put(String key, int value) {DLinkedNode node = cache.get(key);if(node == null){DLinkedNode newNode = new DLinkedNode();newNode.key = key;newNode.value = value;this.cache.put(key, newNode);this.addNode(newNode);++count;if(count > capacity){// 淘汰栈底元素DLinkedNode tail = this.popTail();this.cache.remove(tail.key);--count;}}else{//该元素已经存在//将该元素移动到栈顶node.value = value;this.moveToHead(node);}}//添加节点private void addNode(DLinkedNode node){node.pre = head;node.next = head.next;head.next.pre = node;head.next = node;}//删除该节点（跳过该节点）private void removeNode(DLinkedNode node){DLinkedNode pre = node.pre;DLinkedNode next = node.next;pre.next = next;next.pre = pre;}//将该节点移动到头节点private void moveToHead(DLinkedNode node){this.removeNode(node);this.addNode(node);}//淘汰栈底元素private DLinkedNode popTail(){DLinkedNode res = tail.pre;this.removeNode(res);return res;}@Overridepublic String toString() {StringBuilder sbu = new StringBuilder();DLinkedNode cur = head.next;sbu.append("{");while (cur != tail) {if (cur.next != tail) {sbu.append(cur.key).append("=").append(cur.value).append(", ");} else {sbu.append(cur.key).append("=").append(cur.value);}cur = cur.next;}sbu.append("}");return sbu.toString();}public static void main(String[] args) {LRUCache lruCache = new LRUCache(3);lruCache.put("1", 5);lruCache.put("2", 2);lruCache.put("3", 1);System.out.println(lruCache);System.out.println("使用后：");lruCache.put("2",2);System.out.println(lruCache);lruCache.put("2",2);System.out.println(lruCache);lruCache.put("4", 13);System.out.println("最不常用的被删除，新元素插到头部：");System.out.println(lruCache);}}
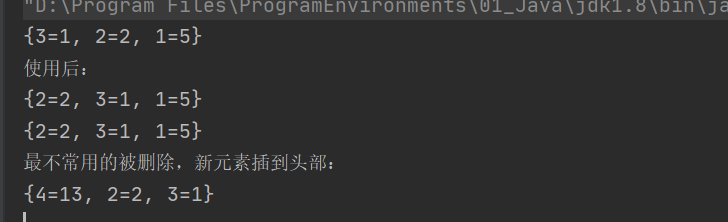
  • 测试结果：

image-20240419181126783

在这里插入图片描述

这篇关于【算法刷题】手撕LRU算法（原理、图解、核心思想）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/927934。

相关文章

Spring核心思想之浅谈IoC容器与依赖倒置(DI)

Spring核心思想之浅谈IoC容器与依赖倒置(DI)

《Spring核心思想之浅谈IoC容器与依赖倒置(DI)》文章介绍了Spring的IoC和DI机制,以及MyBatis的动态代理,通过注解和反射,Spring能够自动管理对象的创建和依赖注入,而MyB... 目录一、控制反转 IoC二、依赖倒置 DI1. 详细概念2. Spring 中 DI 的实现原理三、
阅读更多...
龙蜥操作系统Anolis OS-23.x安装配置图解教程(保姆级)

龙蜥操作系统Anolis OS-23.x安装配置图解教程(保姆级)

《龙蜥操作系统AnolisOS-23.x安装配置图解教程(保姆级)》：本文主要介绍了安装和配置AnolisOS23.2系统，包括分区、软件选择、设置root密码、网络配置、主机名设置和禁用SELinux的步骤，详细内容请阅读本文，希望能对你有所帮助... ‌AnolisOS‌是由阿里云推出的开源操作系统，旨
阅读更多...
Redis主从/哨兵机制原理分析

Redis主从/哨兵机制原理分析

《Redis主从/哨兵机制原理分析》本文介绍了Redis的主从复制和哨兵机制,主从复制实现了数据的热备份和负载均衡,而哨兵机制可以监控Redis集群,实现自动故障转移,哨兵机制通过监控、下线、选举和故... 目录一、主从复制1.1 什么是主从复制1.2 主从复制的作用1.3 主从复制原理1.3.1 全量复制
阅读更多...
Python中的随机森林算法与实战

Python中的随机森林算法与实战

《Python中的随机森林算法与实战》本文详细介绍了随机森林算法,包括其原理、实现步骤、分类和回归案例,并讨论了其优点和缺点,通过面向对象编程实现了一个简单的随机森林模型,并应用于鸢尾花分类和波士顿房... 目录1、随机森林算法概述2、随机森林的原理3、实现步骤4、分类案例：使用随机森林预测鸢尾花品种4.1
阅读更多...
Redis主从复制的原理分析

Redis主从复制的原理分析

《Redis主从复制的原理分析》Redis主从复制通过将数据镜像到多个从节点,实现高可用性和扩展性,主从复制包括初次全量同步和增量同步两个阶段,为优化复制性能,可以采用AOF持久化、调整复制超时时间、... 目录Redis主从复制的原理主从复制概述配置主从复制数据同步过程复制一致性与延迟故障转移机制监控与维
阅读更多...
SpringCloud配置动态更新原理解析

SpringCloud配置动态更新原理解析

《SpringCloud配置动态更新原理解析》在微服务架构的浩瀚星海中,服务配置的动态更新如同魔法一般,能够让应用在不重启的情况下,实时响应配置的变更,SpringCloud作为微服务架构中的佼佼者,... 目录一、SpringBoot、Cloud配置的读取二、SpringCloud配置动态刷新三、更新@R
阅读更多...
Redis主从复制实现原理分析

Redis主从复制实现原理分析

《Redis主从复制实现原理分析》Redis主从复制通过Sync和CommandPropagate阶段实现数据同步,2.8版本后引入Psync指令,根据复制偏移量进行全量或部分同步,优化了数据传输效率... 目录Redis主DodMIK从复制实现原理实现原理Psync: 2.8版本后总结Redis主从复制实
阅读更多...
不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
康拓展开（hash算法中会用到）

康拓展开（hash算法中会用到）

康拓展开是一个全排列到一个自然数的双射（也就是某个全排列与某个自然数一一对应） 公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。（a[i]在不同应用中的含义不同）； 典型应用： 计算当前排列在所有由小到大全排列中的顺序，也就是说求当前排列是第
阅读更多...
深入探索协同过滤：从原理到推荐模块案例

深入探索协同过滤：从原理到推荐模块案例

文章目录 前言一、协同过滤1. 基于用户的协同过滤（UserCF）2. 基于物品的协同过滤（ItemCF）3. 相似度计算方法 二、相似度计算方法1. 欧氏距离2. 皮尔逊相关系数3. 杰卡德相似系数4. 余弦相似度 三、推荐模块案例1.基于文章的协同过滤推荐功能2.基于用户的协同过滤推荐功能 前言     在信息过载的时代，推荐系统成为连接用户与内容的桥梁。本文聚焦于
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2