本文主要是介绍机器学习笔记(一)ROC与AUC的定义与概念,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
综述
ROC综述为“受试者工作特征”(Receiver Operation Characteristic),其对于组织分类器和将分类器的性能可视化十分有用。
它最先由二战的电子工程师发明,用于侦测战场上的敌军载具,是信号检测理论的重要组成部分,最近经常用于机器学习和数据挖掘研究,可以用于:(1)选择最优的分类模型(2)在模型中设置最佳阈值
二分类常用公式
首先我们给出真阳性(true positive)、假阳性(false positive)、真阴性(true negative)和假阴性(false negative)的定义:
| 真实结果↓预测结果→ | 正例 | 反例 |
|---|---|---|
| 正例 | TP(真阳性) | FN(假阴性) |
| 反例 | FP(假阳性) | TN(真阴性) |
若为二元分类模型,则两类分别对应阳性和阴性;若是连续值则我们需要设置一个阈值,通过与这一个阈值比较来确定阴阳性。
我们定义真阳性率 T P R TPR TPR 和伪阳性率 F P R FPR FPR 如下:
T P R = T P P = T P T P + F N \large{TPR = \frac{TP}{P} = \frac{TP}{TP + FN}} TPR=PTP=TP+FNTP
F P R = F P N = F P F P + T N \large{FPR = \frac{FP}{N} = \frac{FP}{FP + TN}} FPR=NFP=FP+TNFP
类似,我们还有以下:
准确率 A C C = T P + T N P + N \large{ACC = \frac{TP + TN}{P + N}} ACC=P+NTP+TN
真阴性率 T N R = T N F P + T N TNR = \large{\frac{TN}{FP+TN}} TNR=FP+TNTN
阴性预测值 N P V = T N T N + F N \large{NPV=\frac{TN}{TN+FN}} NPV=TN+FNTN
阳性预测值 P P V = T P T P + F R \large{PPV=\frac{TP}{TP+FR}} PPV=TP+FRTP
假发现率 F D R = F P F P + T P \large{FDR=\frac{FP}{FP+TP}} FDR=FP+TPFP
ROC曲线绘制
我们以 T P R TPR TPR(真阳性率)和 F P R FPR FPR(伪阴性率)为纵轴和横轴,绘制ROC曲线:
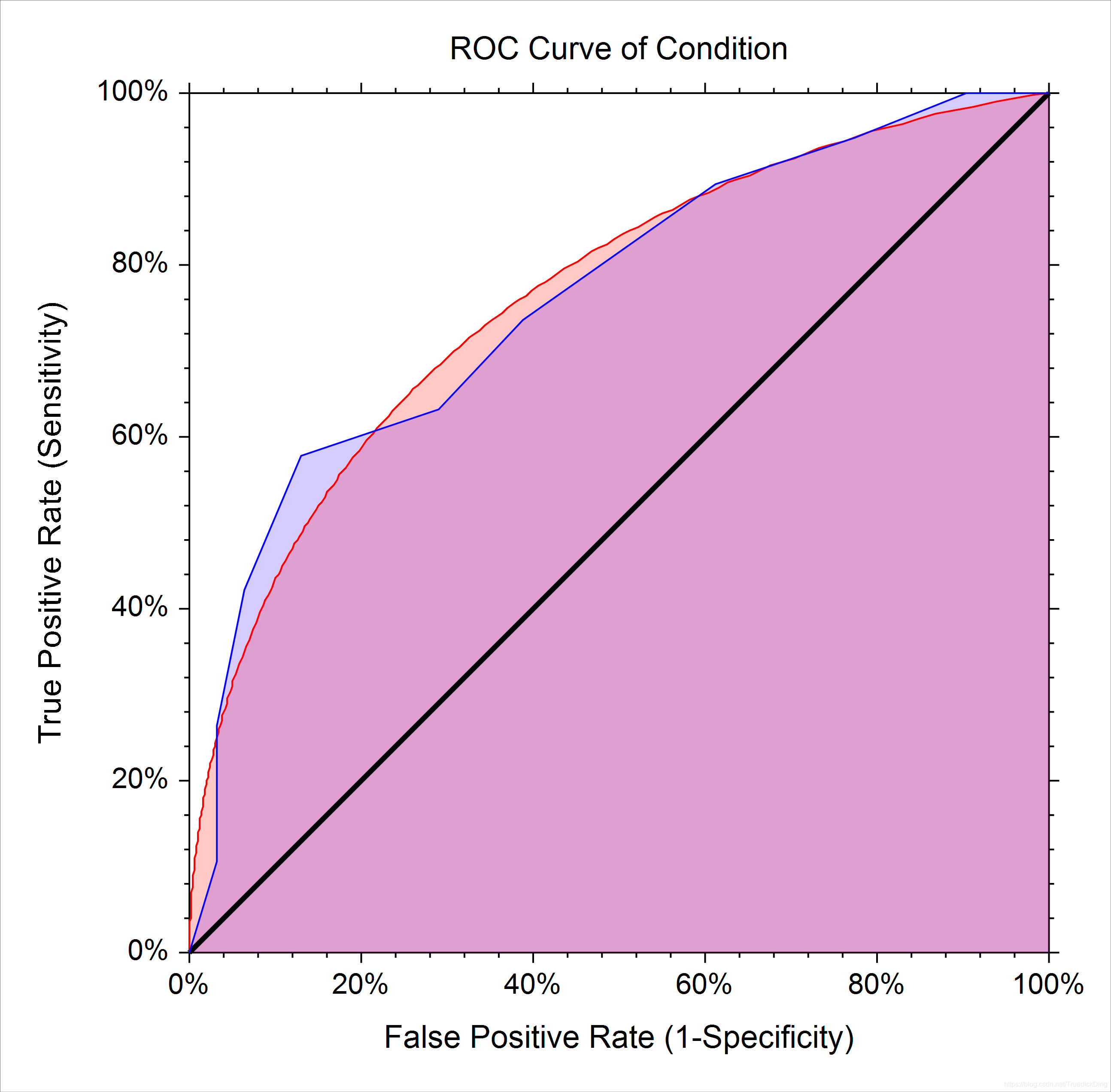
若我们的样例数是有限的,则我们可以通过以下步骤绘制近似ROC图:
我们设前一个标记点坐标为 ( x , y ) (x, y) (x,y),若当前为真阳性( T P TP TP),则当前坐标为 ( x , y + 1 m + ) (x, y+\frac{1}{m^+}) (x,y+m+1),若当前为伪阳性( F P FP FP),则当前坐标为 ( x + 1 m − , y ) (x+\frac{1}{m^-}, y) (x+m−1,y)
若一个学习器的ROC曲线将另一个学习器的ROC曲线完全“包住”,则后者的性能优于前者;在交叉的情况下,我们通过判断ROC曲线下面的面积来判断学习器的优劣,故有了AUC的定义
AUC的定义与概念
AUC(Area under the Curve of ROC),顾名思义,其值为ROC曲线下面的面积
假定ROC曲线是由坐标为 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . . , ( x m , y m ) } \{(x_1, y_1), (x_2, y_2), ....,(x_m, y_m)\} {(x1,y1),(x2,y2),....,(xm,ym)}的点按序连接成的 ( x 1 = 0 , x m = 1 ) (x_1 = 0, x_m=1) (x1=0,xm=1),则AUC可估算为
A U C = 1 2 ∑ i = 1 m − 1 ( x i + 1 − x i ) ⋅ ( y i + y i + 1 ) \large{AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_{i})\cdot(y_i+y_{i+1})} AUC=21∑i=1m−1(xi+1−xi)⋅(yi+yi+1)
根据AUC判断分类器优劣如下:
- A U C = 1 AUC=1 AUC=1,完美的分类器,对于这一个预测模型,至少存在一个阈值能够得到完美预测
- 0.5 < A U C < 1 0.5<AUC<1 0.5<AUC<1,由于随机预测,可以通过妥善设置阈值来提高预测价值
- A U C = 0.5 AUC=0.5 AUC=0.5,与随机预测一样,模型无预测价值
- A U C < 0.5 AUC<0.5 AUC<0.5,比随机预测还差,但是可以通过反预测而行来进行设置
参考资料
- ROC曲线 - 维基百科,自由的百科全书
- 《机器学习》- 周志华
这篇关于机器学习笔记(一)ROC与AUC的定义与概念的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






