本文主要是介绍机器学习中PCA和ICA的理解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在高维数据处理中,为了简化计算量以及储存空间,需要对这些高维数据进行一定程度上的降维,并尽量保证数据的不失真。PCA和ICA是两种常用的降维方法。PCA:principal component analysis ,主成分分析
ICA :Independent component analysis,独立成分分析
PCA,ICA都是统计理论当中的概念,在机器学习当中应用很广,比如图像,语音,通信的分析处理。
PCA是找出信号当中的不相关部分(正交性),对应二阶统计量分析。PCA的实现一般有两种,一种是用特征值分解去实现的,一种是用奇异值(SVD)分解去实现。特征值分解也有很多的局限,比如说变换的矩阵必须是方阵,SVD没有这个限制。
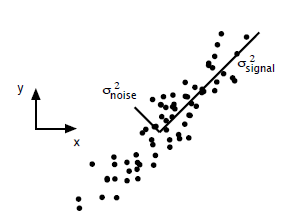
PCA的问题其实是一个基的变换,使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量,我们在讲一个东西的稳定性的时候,往往说要减小方差,如果一个模型的方差很大,那就说明模型不稳定了。但是对于我们用于机器学习的数据(主要是训练数据),方差大才有意义,不然输入的数据都是同一个点,那方差就为0了,这样输入的多个数据就等同于一个数据了。
ICA是找出构成信号的相互独立部分(不需要正交),对应高阶统计量分析。ICA理论认为用来观测的混合数据阵X是由独立元S经过A线性加权获得。ICA理论的目标就是通过X求得一个分离矩阵W,使得W作用在X上所获得的信号Y是独立源S的最优逼近,该关系可以通过下式表示:
ICA相比与PCA更能刻画变量的随机统计特性,且能抑制高斯噪声。
从线性代数的角度去理解,PCA和ICA都是要找到一组基,这组基张成一个特征空间,数据的处理就都需要映射到新空间中去。
两者常用于机器学习中提取特征后的降维操作
这篇关于机器学习中PCA和ICA的理解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!