本文主要是介绍代码随想录第42天|416. 分割等和子集,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
416. 分割等和子集
416. 分割等和子集 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集_哔哩哔哩_bilibili
给你一个 只包含正整数 的 非空 数组
nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。示例 1:
输入:nums = [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。示例 2:
输入:nums = [1,2,3,5] 输出:false 解释:数组不能分割成两个元素和相等的子集。提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了。
该题中的元素只能使用一次,所以是01背包问题。
背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值。
动规五部曲:
1、确定dp数组以及下标的含义:dp[j]表示:容量为j的背包,所背物品的最大价值也为dp[j];
2、确定递推公式:dp[j]=max(dp[j] + dp[j]-weight[i]+value[i]),本题中:nums[i] = val[i], 所以:dp[j] = max(dp[j]+dp[j-nums[i]]+num[i])
3、dp数组如何初始化:dp[0] = 0;非0下标的元素初始为0;
4、确定遍历顺序:一维dp数组的循环中,物品在外,背包在内;
5、举例推导dp数组:
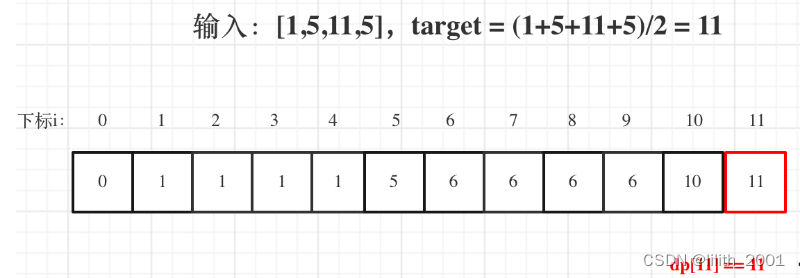
综合代码:
class Solution {public boolean canPartition(int[] nums) {if(nums == null || nums.length == 0) return false;int n = nums.length;int sum = 0;for(int num : nums) {sum += num;}//总和为奇数,不能平分if(sum % 2 != 0) return false;int target = sum / 2;int[] dp = new int[target + 1];for(int i = 0; i < n; i++) {for(int j = target; j >= nums[i]; j--) {//物品 i 的重量是 nums[i],其价值也是 nums[i]dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}//剪枝一下,每一次完成內層的for-loop,立即檢查是否dp[target] == target,優化時間複雜度(26ms -> 20ms)if(dp[target] == target)return true;}return dp[target] == target;}
}这篇关于代码随想录第42天|416. 分割等和子集的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





