CCF-CSP真题《202312-3 树上搜索》思路+c++满分题解

本文主要是介绍CCF-CSP真题《202312-3 树上搜索》思路+c++满分题解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

想查看其他题的真题及题解的同学可以前往查看：CCF-CSP真题附题解大全

问题描述

试题编号：	202312-3
试题名称：	树上搜索
时间限制：	1.0s
内存限制：	512.0MB
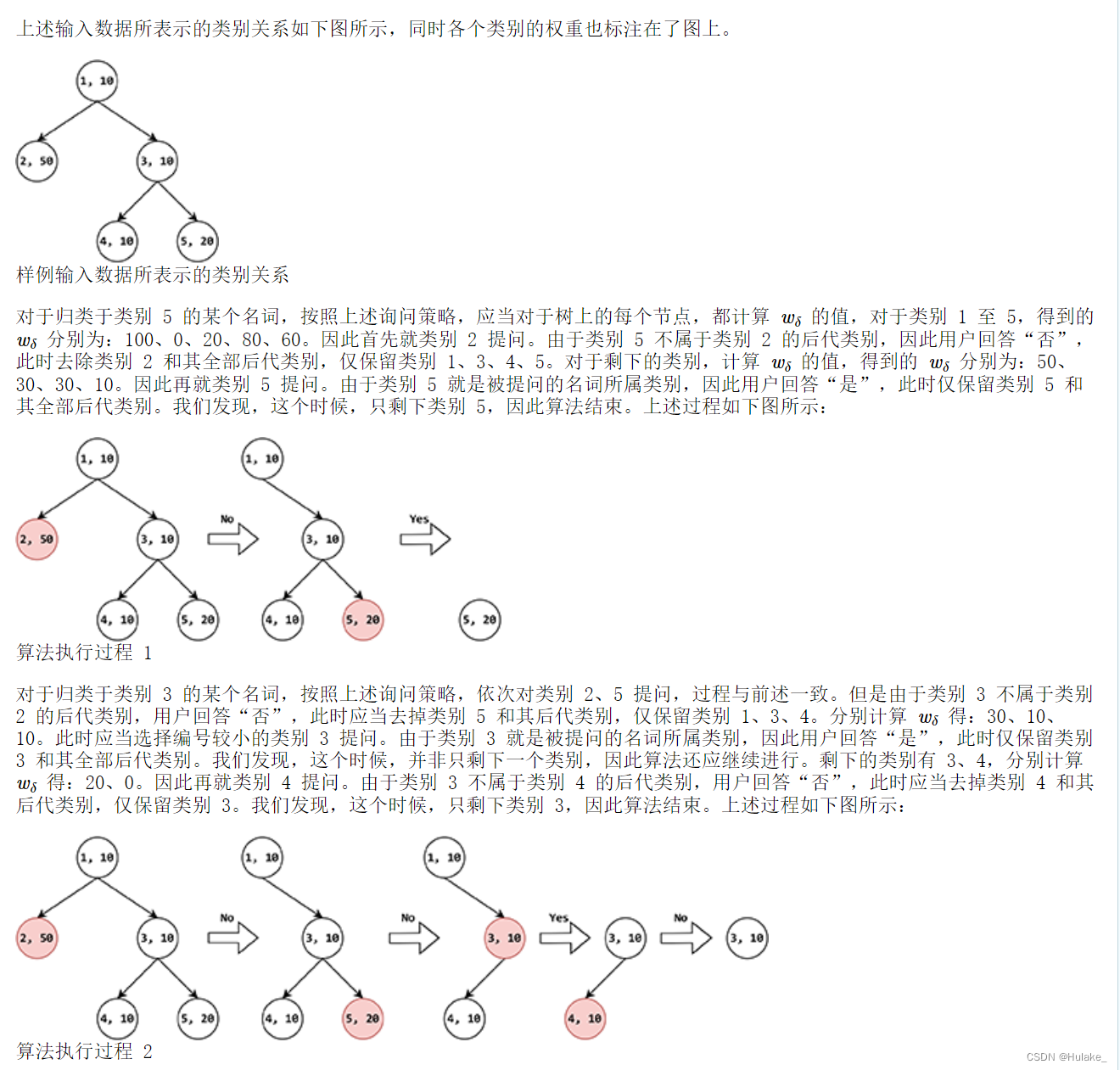
问题描述：	题目背景问题描述输入格式输出格式样例1输入 5 2 10 50 10 10 20 1 1 3 3 5 3 样例1输出 2 5 2 5 3 4 样例解释子任务

真题来源：树上搜索

感兴趣的同学可以如此编码进去进行练习提交

c++满分题解：

#include <bits/stdc++.h>
using  namespace std;
inline long long read()
{long long x = 0, f = 1;char c = getchar();while (c < '0' || c > '9'){if (c == '-') f = -1;c = getchar();}while ( c >= '0' && c <= '9'){x = x * 10 + c - '0';c = getchar();}return x * f;
}struct Node
{long long Weight;long long WeightSum;long long Index;bool IsOut;Node* Child, * Brother, * Above, * LastChild, * PrevBrother;Node(long long Weigh, long long i) : Weight(Weigh), Child(nullptr), LastChild(nullptr), Above(nullptr), Brother(nullptr), WeightSum(Weigh), PrevBrother(nullptr), Index(i) {}
};Node* Nodes[2010];void LinkNode(Node* Parent, Node* Child)
{if (!Parent || !Child) return;Child->Above = Parent;if (!Parent->Child){Parent->Child = Child;Parent->LastChild = Child;return;}Parent->LastChild->Brother = Child;Child->PrevBrother = Parent->LastChild;Parent->LastChild = Child;
}long long AccWeights(Node* CurRoot)
{if (!CurRoot) return 0;CurRoot->WeightSum = CurRoot->Weight;Node* CurNode = CurRoot->Child;while (CurNode){CurRoot->WeightSum += AccWeights(CurNode);CurNode = CurNode->Brother;}return CurRoot->WeightSum;      
}bool HasTarIndex(Node* Root, long long Tar)
{if (!Root) return 0;else if (Root->Index == Tar) return 1;Node* CurNode = Root->Child;while(CurNode){if (HasTarIndex(CurNode, Tar)) return 1;CurNode = CurNode->Brother;}return 0;
}long long RemovedParents[2010]{-1}, RemovedChilds[2010]{-1};
long long RemovedPairs = 0;
void RemoveNode(Node* TarNode)
{if (!TarNode) return;if (!TarNode->PrevBrother) TarNode->Above->Child = TarNode->Brother;else TarNode->PrevBrother->Brother = TarNode->Brother;if (!TarNode->Brother) TarNode->Above->LastChild = TarNode->PrevBrother;else TarNode->Brother->PrevBrother = TarNode->PrevBrother;TarNode->Above = nullptr;TarNode->Brother = nullptr;TarNode->PrevBrother = nullptr;
}
void ReBuild()
{for (long long i = 0; i < RemovedPairs; ++i) LinkNode(Nodes[RemovedParents[i]], Nodes[RemovedChilds[i]]);RemovedPairs = 0;
}
long long GetDelta(Node* TarNode, long long& CurTotalWeight)
{if(!TarNode) return 114514;else if (!TarNode->Above) return TarNode->WeightSum;return abs(CurTotalWeight - 2 * TarNode->WeightSum);
}
long long CurMin = 0, CurIdx = 0;
void Bianli(Node* CurRoot, long long& CurTotalWeight)
{if (!CurRoot) return;long long Delta = GetDelta(CurRoot, CurTotalWeight);//cout << CurRoot->Index << ' '<<Delta<<'\n';if (Delta < CurMin || (CurMin == Delta && CurRoot->Index < CurIdx)){CurMin = Delta;CurIdx = CurRoot->Index;}Node* CurNode = CurRoot->Child;while (CurNode){Bianli(CurNode, CurTotalWeight);CurNode = CurNode->Brother;}
}
void PrintTree(Node* CurRoot)
{if (!CurRoot) return;cout << CurRoot->Index << '\n';Node* CurNode = CurRoot->Child;while (CurNode){cout << '\t' << CurNode->Index << '\n';system("pause");CurNode = CurNode->Brother;}CurNode = CurRoot->Child;while (CurNode){PrintTree(CurNode);CurNode = CurNode->Brother;}
}
int main()
{long long n = read(), m = read();for (long long i = 1; i<= n; ++i) Nodes[i] = new Node(read(), i);for (long long i = 2; i <= n; ++i) LinkNode(Nodes[read()], Nodes[i]);long long Index = 0;for (long long i = 1; i <= m; ++i){RemovedPairs = 0;Index = read();Node* CurRoot = Nodes[1];while(CurRoot->Child){/*cout << "___________________\n";PrintTree(CurRoot);cout << "___________________\n";*/long long SumWeight = AccWeights(CurRoot);CurMin = SumWeight, CurIdx = 0;Bianli(CurRoot, SumWeight);cout << CurIdx << ' ';if (HasTarIndex(Nodes[CurIdx], Index)) CurRoot = Nodes[CurIdx];else{RemovedParents[RemovedPairs] = Nodes[CurIdx]->Above->Index;RemovedChilds[RemovedPairs] = Nodes[CurIdx]->Index;++RemovedPairs;RemoveNode(Nodes[CurIdx]);}}ReBuild();cout << '\n';}for (long long i = 1; i<= n; ++i) delete Nodes[i];
}

运行结果：