本文主要是介绍皇后之战:揭秘N皇后问题的多维解法与智慧【python 力扣52题】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。
会一些的技术:数据分析、算法、SQL、大数据相关、python
欢迎加入社区:码上找工作
作者专栏每日更新:
LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化:企业实战案例
备注说明:方便大家阅读,统一使用python,带必要注释,公众号 数据分析螺丝钉 一起打怪升级
题目描述
给定一个整数 n,返回 n×n 棋盘上的 N 皇后问题的不同解决方案的数量。
每一种解法包含一个明确的 n×n 棋盘上的皇后放置方式,其中 'Q' 代表一个皇后,而 '.' 代表空位。每个皇后都必须满足不能与其他皇后在同一行、同一列或同一对角线上。
输入格式
- n:一个整数,表示棋盘的大小。
输出格式
- 返回所有独特的
n皇后问题的解决方案数量。
示例
示例 1
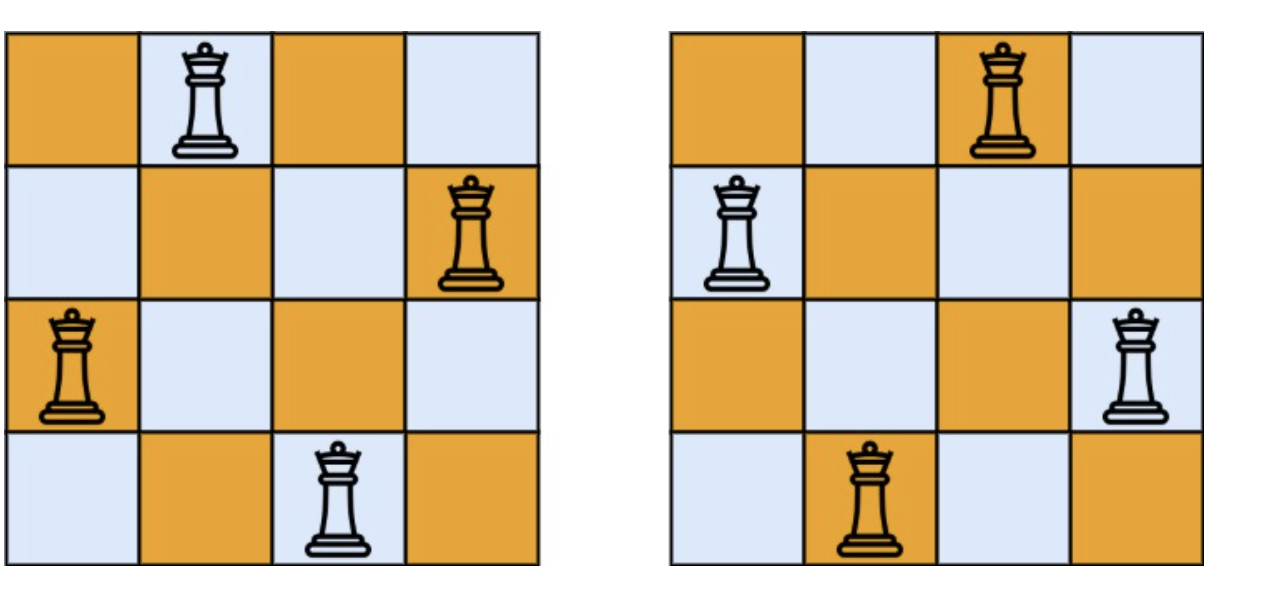
输入: n = 4
输出: 2
示例 2
输入: n = 1
输出: 1
注意
LeetCode题目51 "N皇后"与题目52 "N皇后II"虽然都是基于经典的N皇后问题,但两者的主要区别在于输出的需求不同:
N皇后 (题目 51)
- 目标:找出所有可能的N皇后解决方案的具体棋盘布局。
- 输出:返回所有解决方案,每个解决方案都详细展示了皇后的具体摆放位置。每个解决方案是一个包含n个字符串的列表,每个字符串长度为n,表示棋盘的一行,其中’Q’表示皇后,'.'表示空位。
- 解法关注点:除了求解算法的有效性外,还需要关注如何构造并展示完整的棋盘布局。
N皇后 II (题目 52)
- 目标:仅计算N皇后问题的不同解决方案数量。
- 输出:返回解决方案的数量,而不是具体的棋盘布局。
- 解法关注点:主要关注于优化算法的效率以快速计算出解决方案的总数,而不需要构造棋盘的具体布局。
解法对比
尽管两个问题在解法上可能使用类似的技术(如回溯法),51题需要更多的空间和逻辑来存储和展示所有可能的棋盘配置,而52题则更注重于计数优化,可能会使用更加精简的数据结构(如位运算)来加速计数过程。
方法一:回溯算法
解题步骤
- 初始化变量:创建一个用于存储当前行皇后位置的列表。
- 定义回溯函数:递归定义函数以尝试每一行的每个位置。
- 合法性检查:检查当前位置放置皇后是否合法,即检查列和两个方向的对角线。
- 递归与计数:递归地放置下一个皇后,如果完成一种有效布局则增加计数。
完整的规范代码
def totalNQueens(n):"""计算 n 皇后问题的解决方案总数:param n: int, 棋盘大小:return: int, 解决方案总数"""def backtrack(row, diagonals, anti_diagonals, cols):if row == n:nonlocal countcount += 1returnfor col in range(n):curr_diagonal = row - colcurr_anti_diagonal = row + colif (col in cols or curr_diagonal in diagonals or curr_anti_diagonal in anti_diagonals):continuecols.add(col)diagonals.add(curr_diagonal)anti_diagonals.add(curr_anti_diagonal)backtrack(row + 1, diagonals, anti_diagonals, cols)cols.remove(col)diagonals.remove(curr_diagonal)anti_diagonals.remove(curr_anti_diagonal)count = 0backtrack(0, set(), set(), set())return count# 示例调用
print(totalNQueens(4)) # 输出: 2
算法分析
- 时间复杂度:(O(n!)),尽管有剪枝,每层递归的选择数接近
n。 - 空间复杂度:(O(n)),递归栈深度加用于存储状态的空间。
方法二:位运算优化的回溯算法
解题步骤
- 位运算优化:使用位运算代替集合操作,提高效率。
- 定义位运算回溯函数:使用位掩码表示列和对角线的占用状态,通过位运算快速检查和修改状态。
- 递归与计数:递归放置皇后,完成布局时增加解决方案计数。
完整的规范代码
def totalNQueens(n):"""计算 n 皇后问题的解决方案总数,使用位运算进行优化:param n: int, 棋盘大小:return: int, 解决方案总数"""def solve(row, hills, next_row, dales):if row == n:nonlocal countcount += 1returnfree_columns = columns & ~(hills | next_row | dales)while free_columns:curr_column = -free_columns & free_columnssolve(row + 1, (hills | curr_column) << 1, next_row | curr_column, (dales | curr_column) >> 1)free_columns &= free_columns - 1columns = (1 << n) - 1count = 0solve(0, 0, 0, 0)return count# 示例调用
print(totalNQueens(4)) # 输出: 2
算法分析
- 时间复杂度:(O(n!)),位运算显著提高了效率,但最坏情况下仍需尝试所有可能。
- 空间复杂度:(O(n)),递归深度决定了空间复杂度,虽然使用位运算减少了空间占用。
方法三:迭代回溯
解题步骤
- 使用栈模拟递归:使用栈来模拟递归过程,避免函数调用的开销。
- 迭代处理:在迭代中管理棋盘状态和递归变量,以模拟递归调用栈的行为。
完整的规范代码
def totalNQueens(n):"""使用迭代回溯解决 n 皇后问题:param n: int, 棋盘大小:return: int, 解决方案总数"""stack = [(0, 0, 0, 0)] # (row, hills, next_row, dales)count = 0while stack:row, hills, next_row, dales = stack.pop()if row == n:count += 1continuefree_columns = ((1 << n) - 1) & ~(hills | next_row | dales)while free_columns:curr_column = -free_columns & free_columnsstack.append((row + 1, (hills | curr_column) << 1, next_row | curr_column, (dales | curr_column) >> 1))free_columns &= free_columns - 1return count# 示例调用
print(totalNQueens(4)) # 输出: 2
算法分析
- 时间复杂度:(O(n!)),迭代的方式减少了递归调用开销,但仍然需要尝试所有可能的放置方式。
- 空间复杂度:(O(n)),虽然使用栈来模拟递归,但空间复杂度与递归方法相当。
不同算法的优劣势对比
| 特征 | 方法一: 回溯算法 | 方法二: 位运算优化回溯 | 方法三: 迭代回溯 |
|---|---|---|---|
| 时间复杂度 | (O(n!)) | (O(n!)) | (O(n!)) |
| 空间复杂度 | (O(n)) | (O(n)) | (O(n)) |
| 优势 | - 易于理解和实现 | - 空间效率高 | - 避免递归调用开销 |
| 劣势 | - 空间消耗较大 | - 理解和实现较为复杂 | - 状态维护较为复杂 |
应用示例
科学研究:
N皇后问题常用于算法研究和教学,特别是在探讨组合数学、算法优化、复杂度分析等领域。此问题的不同解决策略可用于教授递归、回溯及其优化。
算法竞赛:
在算法竞赛中,N皇后问题是经典问题,经常出现在各类比
赛和面试中,作为测试程序员解决复杂问题能力的一种方式。
通过以上方法和示例,可以深入理解和掌握N皇后问题的多种解决方案及其应用场景。这些技术不仅限于此问题,还可广泛应用于其他需要递归和回溯解决的问题中。
这篇关于皇后之战:揭秘N皇后问题的多维解法与智慧【python 力扣52题】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






