哈夫曼编码压缩解压缩实现不同类型文件压缩比的测试

本文主要是介绍哈夫曼编码压缩解压缩实现不同类型文件压缩比的测试，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

压缩原理及步骤&&压缩比的计算

压缩原理及步骤

压缩的第一步：

将一个文件以各个字符出现的次数为权值建立哈夫曼树，这样每个字符可以用从树根到该字符所在到叶子节点的路径来表示。(左为0,右为1)

压缩第二步：

哈夫曼编码有一个很重要的特性：每个字符编码不会成为另一个编码的前缀。这个特性保证了即使我们把不同长度的编码存在一起，仍然也可以把它们分离开，不会出现认错人的冲突。
那么我们就可以把所有的字符按照原有顺序用其编码替换，构建新的字符串作为其压缩后的串。

压缩第三步：

有的小伙伴可能要问了，这样一搞不是越变越多了么，哪是什么压缩。哈哈，大部分孩子可能已经想到啦，既然单位编码除了0就是1为什么还要用字节来存呢，用位来保存，8个单位编码为1位。这样转化完成后的串才是真正压缩后的串。

当然，因为我们还要进行解压，所以这里构建的树也要和串一并加入到文件。

压缩比的计算

介绍完步骤，我们来计算一下哈夫曼编码的压缩比。 用len表示串长度，path(i)表示每i个字符的编码长度，那么根据上文所介绍的原理，我们可以很容易知道，串通过哈夫曼压缩后的长度为

sum(path(i)) 1<=i<=len

这个式子虽然正确但不能直观的感受的压缩比，所以我们来假设一种平均情况进行估算假如一个 串长度为n，一共包含 m个不同的字符，那么所构建成的哈夫曼树的 总结点数为 2*m-1。假设，n很大，那么可以忽略树的保存所占用的空间。如果假设此串中每个字符出现的次数都是相同的，那么也可以假设，它们所生成的哈夫曼树是完全二叉树. 即每个叶子(字符)的 深度为log(m)+1，则路径长度为log(m)。log(m)即为该串字符的平均路径长度，那么压缩后的串长为log(m)/8。由上可以得出平均压缩比的公式为：

n*log(2*m-1)/8/n = log(2*m-1)/8;

可见压缩比的大小主要与m有关，即不同的字符越少越好。 ascii码的范围为0～255，共有256种不同字符，代入上式得

log(2*256-1) ＝ 6.23 …
向上取整为7(路径个数哪有小数)
7/8 = 0.875 = %87.5
所以哈夫曼编码的平均压缩比为%87.5。

强调

上述的假设在计算情况中忽略了对哈夫曼树的保存，所以只在文件总长度与不同字符总数相差很大时才生效。

考虑ascii码外的其它语言

一开始为考虑这个钻了牛角尖，想着去统一用wchar_t保存或是转为Unicode等等什么的。但其实不必那么复杂，因为汉字(不仅仅汉字，任何字符都是这样的)都是以字节为单位的，由多个字节组成的，将其分开对待，因为最终解压时恢复原串还是按照原有顺序组装，所以和纯英文文件的实现没有什么区别)；

需要注意的地方

所有字符路径的总长不一定整除8，所以在按为保存时，要注意最后一项不足8的情况，进行补零，且要将补零的个数保存起来。

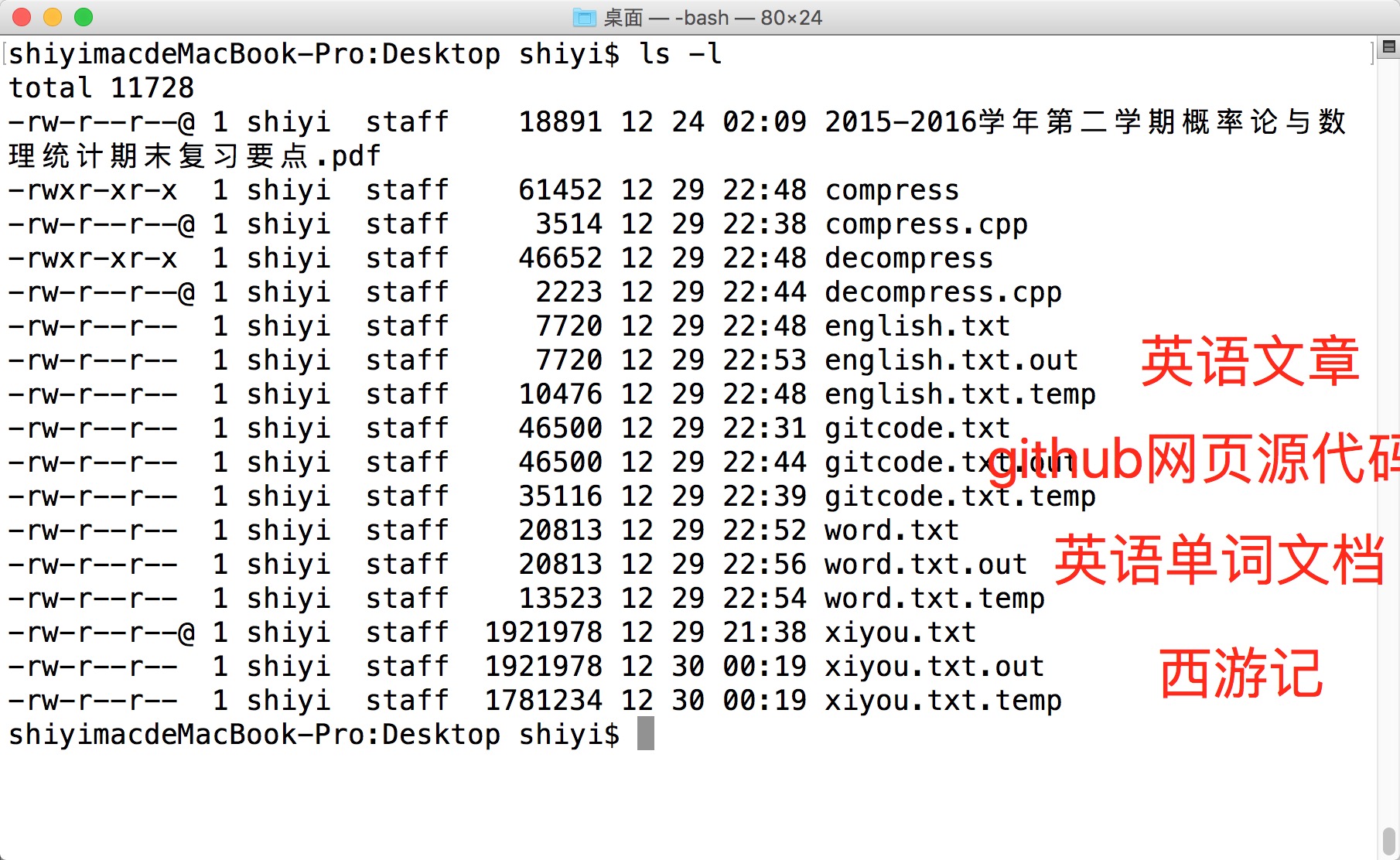
代码对不同类型文档的压缩比测试情况

英语文章

样例文档：西游记英文节选

原大小：7720
压缩后：10476
压缩比：1.356 – %135
此处的文件压缩后不降反增，因为文件本身大小与不同字符的数量相差并不大，加上对树的保存后，空间大于压缩前。

纯汉语文档

样例文档：西游记
原大小：1921978
压缩后：1781234
压缩比：0.926 – %92
不同汉字的数量多。

程序代码

样例文档：github网页源代码
原大小：46500
压缩后：35116
压缩比：0.755 – %76
源代码中全是英文字母与符号，不超过100种，总大小与其相差近500倍，且代码重复词比较多。

英语单词文档

样例文档：英语单词5000
原大小：20813
压缩后：13523
压缩比：0.649 – %65

测试情况

源代码

压缩程序源文件 compress.cpp

#include <iostream>
#include <locale>
#include <cstdlib>
#include <fstream>
#include <vector>
#include <queue>using namespace std;const long long MAX_SIZE = 10000000000;//
const int MAX_TYPE = 300;
unsigned int *f = new unsigned int[MAX_TYPE];//计数
unsigned int *p = new unsigned int[MAX_TYPE];//计下标
char *v = new char[MAX_TYPE];
char filename[20];
char *s[MAX_TYPE];struct Node
{unsigned int weight, parent, lson, rson;Node(){};
}HuffmanTree[MAX_TYPE<<1];struct NodeCmp
{bool operator()(int a, int b){return HuffmanTree[a].weight > HuffmanTree[b].weight;}
};int CreatTree(char *str, long long len)
{int num = 1;for(int i=0;i<len;i++)f[str[i]]++;cout<<"len::"<<len<<endl;for(int i=0;i<len;i++){if(f[str[i]]){HuffmanTree[num].weight = f[str[i]];HuffmanTree[num].lson = 0;HuffmanTree[num].rson = 0;f[str[i]] = 0;if(p[str[i]] == 0)p[str[i]] = num;v[num] = str[i];++num;}}cout<<"num::"<<num<<endl;return num;
}void CodingTree(int num)
{priority_queue<int, vector<int>, NodeCmp> q;for(int i=1;i<num;i++)q.push(i);int len = num;for(int i=0;i<num-2;i++){int x = q.top(); q.pop();int y = q.top(); q.pop();HuffmanTree[len].weight = HuffmanTree[x].weight + HuffmanTree[y].weight;HuffmanTree[x].parent = HuffmanTree[y].parent = len;HuffmanTree[len].lson = y;HuffmanTree[len].rson = x;q.push(len++);}
}void FindPath(int num)
{char *t = new char[num];t[num-1] = '\0';for(int i=1;i<num;i++){int son = i, father = HuffmanTree[i].parent;int start = num-1;while(father != 0){--start;if(HuffmanTree[father].rson == son)t[start] = '1';elset[start] = '0';son = father;father = HuffmanTree[father].parent;}s[i] = new char[num - start];strcpy(s[i], &t[start]);}
}void print(int num, long long len, char *str)
{ofstream fout(filename, ios::out);fout<<num<<endl;for(int i=1;i<num;i++){fout<<s[i]<<endl;fout<<v[i]<<endl;}long long pos = 0;char *ans = new char[MAX_SIZE];int now = 7;for(long long i=0;i<len;i++){int k = 0;while(s[p[str[i]]][k] != '\0'){ans[pos] |= (s[p[str[i]]][k]-'0')<<now--;if(now < 0){now = 7;pos++;}++k;}}int zero = 0;if(now != 7) zero = now%7+1, pos++;fout<<zero<<" "<<pos<<endl;fout.write(ans, sizeof(char)*pos);fout.close();cout<<"zero::"<<zero<<endl;
}int main(int argc, char **argv)
{sprintf(filename, "%s.temp", argv[1]);ifstream fin(argv[1],ios::ate | ios::in);if(!fin){cout<<"File open error!"<<endl;return 0;}long long size = fin.tellg();if(size > MAX_SIZE){cout<<"Too long!"<<endl;return 0;}fin.seekg(0, ios::beg);char *str = new char[size+1];fin.read(str,size);fin.close();int num = CreatTree(str, size);CodingTree(num);FindPath(num);print(num, size, str);return 0;
}

解压程序源文件 compress.cpp

#include <iostream>
#include <locale>
#include <cstdlib>
#include <fstream>
#include <vector>
#include <queue>using namespace std;
char filename[20];
const long long MAX_SIZE = 10000000000;//
const int MAX_TYPE = 300;
struct Node
{char v;int parent, lson, rson;Node(){};
}HuffmanTree[MAX_TYPE<<1];char *str = new char[MAX_SIZE];
char *ans = new char[MAX_SIZE];void CreatTree(char *t, char v, int &pos)
{int root = 0;for(int i=0;t[i]!='\0';i++){if(t[i] == '1'){if(HuffmanTree[root].rson == 0)HuffmanTree[root].rson = pos++;root = HuffmanTree[root].rson;}else{if(HuffmanTree[root].lson == 0)HuffmanTree[root].lson = pos++;root = HuffmanTree[root].lson;}}HuffmanTree[root].v = v;
}void print(int zero, int len, char *str)
{long long start = 0;int root = 0;int end = 0;for(int i=0;i<len;i++){char t = str[i];if(i == len-1)end = zero;for(int j=7;j>=end;j--){if((1<<j) & t)root = HuffmanTree[root].rson;elseroot = HuffmanTree[root].lson;if(HuffmanTree[root].lson == 0 && HuffmanTree[root].rson == 0){ans[start++] = HuffmanTree[root].v;root = 0;}}}cout<<"len::"<<start<<endl;ofstream out(filename, ios::out);out.write(ans, sizeof(char)*(start));out.close();
}int main(int argc, char **argv)
{strcpy(filename, argv[1]);filename[strlen(filename)-4] = 'o';filename[strlen(filename)-3] = 'u';filename[strlen(filename)-2] = 't';filename[strlen(filename)-1] = '\0';ifstream fin(argv[1], ios::in);if(!fin){cout<<"File open error!"<<endl;return 0;}int num;char *t = new char[num];char *v = new char[3];fin>>num;fin.getline(t,num);cout<<"size::"<<num<<endl;int pos = 1;for(int i=1;i<num;i++){fin.getline(t,num);fin.getline(v,num);if(v[0] == '\0'){fin.getline(v,num);v[0] = '\n';    }CreatTree(t, v[0], pos);v[0]=0;}int zero;long long size;fin>>zero; fin>>size;fin.getline(t,num);fin.read(str,sizeof(char)*size);print(zero, size, str);cout<<"zero::"<<zero<<endl;return 0;
}