【机器学习】Q-Learning算法：在序列决策问题中的实践与探索

本文主要是介绍【机器学习】Q-Learning算法：在序列决策问题中的实践与探索，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在人工智能领域，序列决策问题一直是一个核心挑战。面对复杂的环境和动态变化的状态，智能体如何做出最优决策，以达到长期目标，是研究者们关注的焦点。Q-Learning算法作为一种经典的强化学习方法，为我们提供了解决这一问题的有效手段。本文将结合实例和代码，对Q-Learning算法在序列决策问题中的应用进行深入分析。

一、Q-Learning算法概述

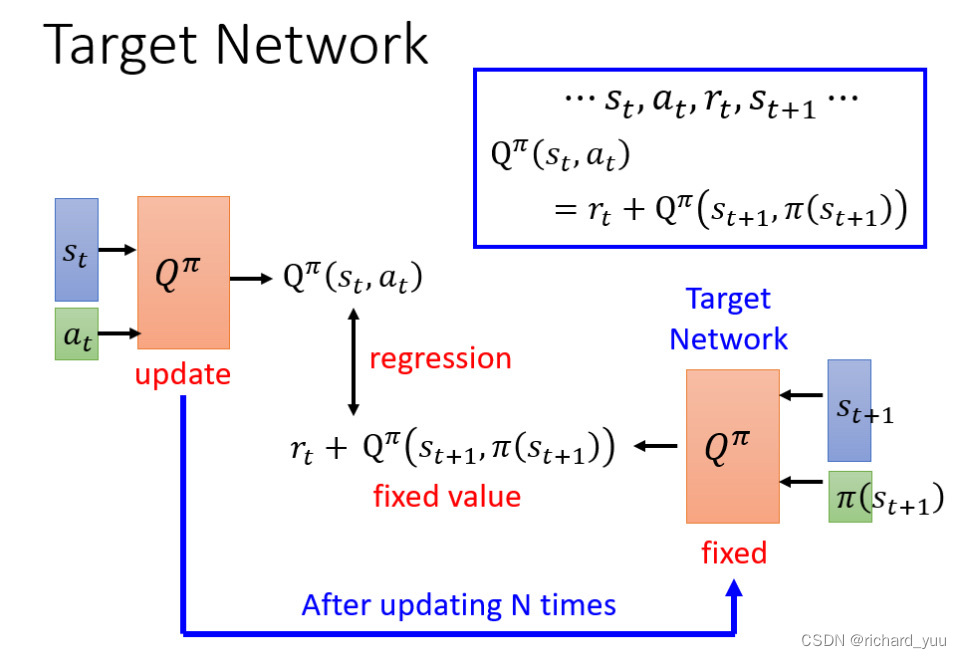
** Q-Learning算法的核心思想是学习一个Q值表，该表记录了在不同状态下采取不同行动所能获得的长期回报**。通过不断更新这个Q值表，智能体能够逐渐学习到最优的行为策略。Q-Learning算法的关键在于其更新规则，即贝尔曼方程的应用。在实际应用中，我们常常采用其简化形式，通过设置学习率α和折扣因子γ来调整更新的步长和未来奖励的权重。

二、Q-Learning算法实例分析

以经典的格子世界问题为例，我们可以直观地展示Q-Learning算法的工作过程。在这个问题中，智能体需要在一个由格子组成的二维环境中，通过一系列行动（如上下左右移动）来找到通往目标格子的最短路径。每个格子代表一个状态，智能体在每个状态下可以选择的行动是固定的（即上下左右移动）。当智能体到达目标格子时，会获得一个正的奖励；如果触碰到障碍物或超出边界，则会受到惩罚。
在这个问题中，我们可以定义一个Q值表来记录每个状态下每个行动的价值。初始时，Q值表中的所有值都设置为零。然后，智能体开始与环境进行交互，根据ε-greedy策略选择行动，并在每个时间步骤中根据贝尔曼方程更新Q值表。随着交互次数的增加，Q值表逐渐收敛，智能体也学会了最优的行为策略。

三、Q-Learning算法代码实现

下面是一个简单的Q-Learning算法的实现代码，用于解决格子世界问题：

pythonimport numpy as np
import random# 设定格子世界的相关参数
NUM_STATES = 25  # 状态总数
NUM_ACTIONS = 4  # 行动总数（上下左右）
EPSILON = 0.1  # 探索率
ALPHA = 0.5  # 学习率
GAMMA = 0.9  # 折扣因子# 初始化Q值表
Q_table = np.zeros((NUM_STATES, NUM_ACTIONS))# 定义奖励函数和状态转移函数（这里省略具体实现）
# reward_function(state, action)
# transition_function(state, action)# Q-Learning算法主循环
for episode in range(1000):  # 训练的总轮数state = 0  # 初始状态while state != NUM_STATES - 1:  # 当未达到目标状态时继续循环if random.random() < EPSILON:  # 以一定概率进行探索action = random.choice(range(NUM_ACTIONS))else:  # 否则选择当前状态下Q值最大的行动action = np.argmax(Q_table[state, :])next_state, reward = transition_function(state, action)Q_predict = Q_table[state, action]if next_state == NUM_STATES - 1:  # 如果到达目标状态，则不再考虑未来的奖励Q_target = rewardelse:Q_target = reward + GAMMA * np.max(Q_table[next_state, :])# 更新Q值表Q_table[state, action] += ALPHA * (Q_target - Q_predict)state = next_state  # 更新当前状态为下一个状态# 输出训练后的Q值表
print(Q_table)

在上面的代码中，我们首先定义了格子世界的参数，包括状态总数、行动总数、探索率、学习率和折扣因子。然后，我们初始化了一个Q值表，并定义了奖励函数和状态转移函数（这里省略了具体实现）。在主循环中，我们模拟了智能体与环境的交互过程，根据ε-greedy策略选择行动，并根据贝尔曼方程更新Q值表。最后，我们输出了训练后的Q值表，可以看到智能体已经学会了在不同状态下选择最优行动的策略。

四、总结与展望

通过本文的分析和实例展示，我们可以看到Q-Learning算法在解决序列决策问题中的有效性和实用性。然而，Q-Learning算法也存在一些局限性，如在高维状态空间或连续动作空间中的应用较为困难。未来，我们可以探索更加高效的算法来应对这些挑战，进一步推动人工智能在序列决策问题中的应用和发展。

这篇关于【机器学习】Q-Learning算法：在序列决策问题中的实践与探索的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---