代码随想录打卡—day27—【回溯】— 回溯基础练习 4.15+4.16

本文主要是介绍代码随想录打卡—day27—【回溯】— 回溯基础练习 4.15+4.16，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 39. 组合总和

 39. 组合总和

我的AC代码：

class Solution {
public:vector<vector<int>> ans;vector<int> path;void dfs(int sum,vector<int>& candidates,int target,int start_idx){if(sum > target)return;if(sum == target){ans.push_back(path);return;}for(int i = start_idx; i < candidates.size();i++){path.push_back(candidates[i]);dfs(sum+candidates[i],candidates,target,i);path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {dfs(0,candidates,target,0);return ans;}
};

看了carl代码，一个什么时候需要startIndex的总结

本题还需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要startIndex呢？

我举过例子，如果是一个集合来求组合的话，就需要startIndex，例如：77.组合 (opens new window)，216.组合总和III (opens new window)。

如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：17.电话号码的字母组合

 优化——加上减枝，就是在打横的for，结束条件上做文章，防止再一次递归之后返回这几步骤。

对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。

class Solution {
public:vector<vector<int>> ans;vector<int> path;void dfs(int sum,vector<int>& candidates,int target,int start_idx){if(sum == target){ans.push_back(path);return;}for(int i = start_idx; i < candidates.size() && sum + candidates[i] <= target;i++){path.push_back(candidates[i]);dfs(sum+candidates[i],candidates,target,i);path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());dfs(0,candidates,target,0);return ans;}
};

2 40. 组合总和 II { 不同层的val相同的可以取，同层的val相同的不可以再次取 }

40. 组合总和 II

carl博客：代码随想录

我自己ac不了，本题目的关键是：

1、树层去重的话，需要对数组排序

2、不同层的val相同的可以取，同层的val相同的不可以再次取

于是我写出这样的代码：

class Solution {
public:vector<vector<int>> ans;vector<int> path;/*不同层的val相同的可以取同层的val相同的不可以再次取*/bool vis[120];void dfs(int sum, vector<int>& candidates, int target,int start_idx){if(sum > target)return;if(sum == target){ans.push_back(path);return;}for(int i = start_idx; i < candidates.size() && sum + candidates[i] <= target;i++){if(!vis[candidates[i]]) // 这一层还没有用过candidates[i]{vis[candidates[i]] = 0;path.push_back(candidates[i]);// for(int j = 0; j < path.size();j++)//     cout << path[j] << ' ';// puts("");dfs(sum+candidates[i],candidates,target,i+1);path.pop_back();vis[candidates[i]] = 1;}else continue;}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());dfs(0,candidates,target,0);return ans;}
};

但是是错的，原因是比如[1,1,2,5,6,7,10] 在第一个分支[1,1,2]中2回溯回来时候vis[2]设为1，即在[1,2]就断了这个分支，所以我写的 “不同层的val相同的可以取，同层的val相同的不可以再次取” 写法错误！

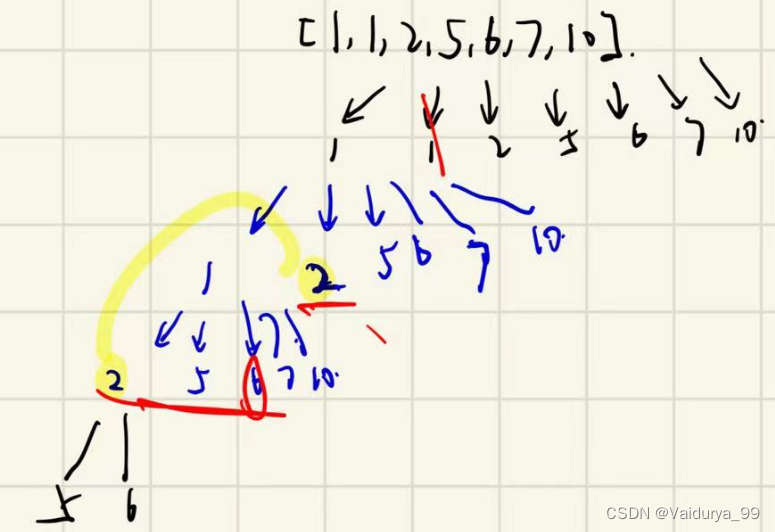
学习carl的写法后：

if(i != 0 && candidates[i] == candidates[i-1] && vis[candidates[i]] == 0)
                continue;

（1）i != 0 第0号元素都不用continue。

（2）candidates[i] == candidates[i-1] && vis[candidates[i]] == 0 本元素和前一个元素val一致，但不在同一分支上在同层中。

（3）candidates[i] == candidates[i-1] && vis[candidates[i]] == 1。本元素和前一个元素val一致，但在同一分支上。

class Solution {
public:vector<vector<int>> ans;vector<int> path;/*不同层的val相同的可以取同层的val相同的不可以再次取*/bool vis[120];void dfs(int sum, vector<int>& candidates, int target,int start_idx){if(sum > target)return;if(sum == target){ans.push_back(path);return;}for(int i = start_idx; i < candidates.size() && sum + candidates[i] <= target;i++){if(i != 0 && candidates[i] == candidates[i-1] && vis[candidates[i]] == 0)continue;vis[candidates[i]] = 1;path.push_back(candidates[i]);  dfs(sum+candidates[i],candidates,target,i+1);  // 同一个数值path.pop_back();vis[candidates[i]] = 0;}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());dfs(0,candidates,target,0);return ans;}
};

3 131. 分割回文串

131. 分割回文串

有问题代码：把它当成各个字母间隔要不要切割的问题，也就是组合问题，思路简单，但是不好实现。

class Solution {
public:vector<vector<string>> ans;vector<string> path;bool is_huiwen(string s){for(int i = 0; i < s.size()/2; i++){if(s[i] == s[s.size() - i - 1])continue;else return 0;}return 1;}void dfs(int u,string s,string now_str){if(u == s.size()){bool ok = 1;for(int i = 0; i < path.size();i++){if(!is_huiwen(path[i])){ok = 0;break;}}if(ok)ans.push_back(path);return;}// 切path.push_back(now_str);string tmp_str = "a";tmp_str[0] =  s[u+1];dfs(u+1,s,tmp_str);path.pop_back();// 不切now_str.push_back(s[u+1]);dfs(u+1,s,now_str);now_str.pop_back();}vector<vector<string>> partition(string s) {if(s.empty())return ans;string tmp = "a";tmp[0] = s[0];dfs(0,s,tmp);return ans;}
};

后来发现我这样写每次调用dfs的前后的字符串的最后一位不好处理，所以改成了只存0101，最后叶子节点再生成对应的字符串切分集合。 这样清晰多了，AC代码如下：

class Solution {
public:vector<vector<string>> ans;vector<int> path;vector<string> str_path;bool is_huiwen(string s){for(int i = 0; i < s.size()/2; i++){if(s[i] == s[s.size() - i - 1])continue;else return 0;}return 1;}void dfs(int u,string s){if(u == s.size() - 1){// 根据0101 得到切分得到str_pathstring tmp = "a";tmp[0] = s[0];for(int i = 0; i < path.size();i++){if(path[i] == 0)tmp += s[i+1];else{str_path.push_back(tmp);tmp = s[i+1];}}str_path.push_back(tmp);bool ok = 1;for(int i = 0; i < str_path.size();i++){if(!is_huiwen(str_path[i])){ok = 0;break;}}if(ok)ans.push_back(str_path);str_path.clear();return;}// 切path.push_back(1);dfs(u+1,s);path.pop_back();// 不切path.push_back(0);dfs(u+1,s);path.pop_back();}vector<vector<string>> partition(string s) {if(s.empty())return ans;ans.clear();path.clear();str_path.clear();dfs(0,s);return ans;}
};

学习carl的代码，比较像之前的老套路，就是现在比如从aab中截取，拆解为：截取了a，再截取ab，类似下面的过程。实现细节中有关键点，比如遍历是挑选[start_idx , i]这样的子串。

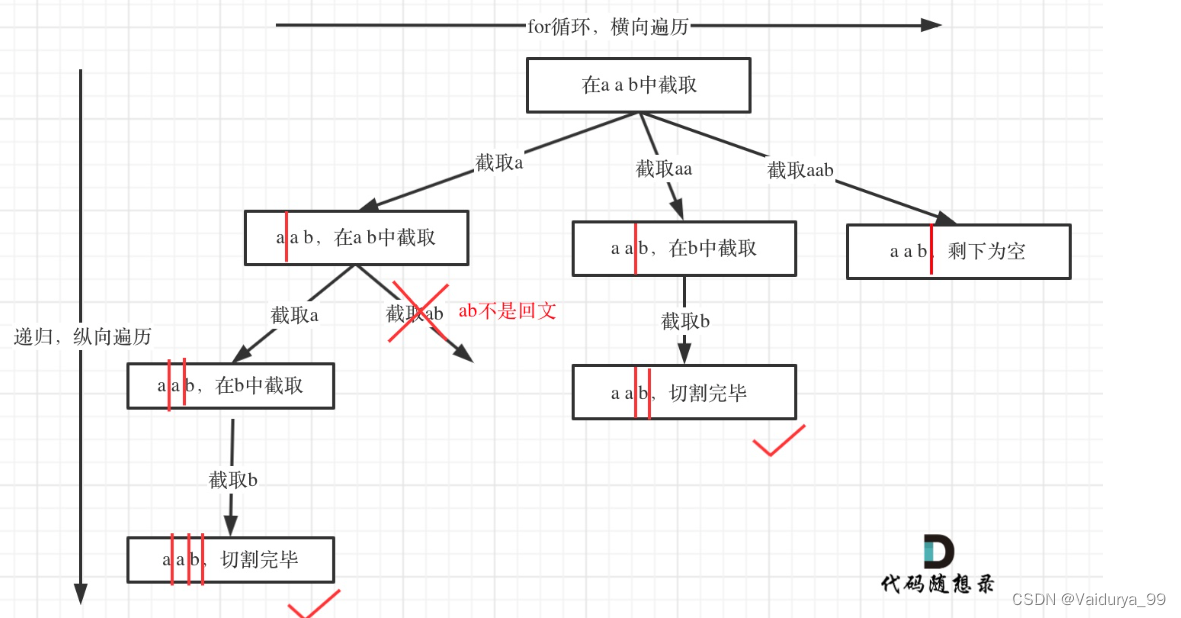
class Solution {
public:vector<vector<string>> ans;vector<string> path;bool is_huiwen(string s){for(int i = 0; i < s.size()/2; i++){if(s[i] == s[s.size() - i - 1])continue;else return 0;}return 1;}void dfs(int start_idx, string s){if(start_idx == s.size()){ans.push_back(path);return;}for(int i = start_idx; i < s.size();i++){string tmp = s.substr(start_idx,i - start_idx + 1);if(is_huiwen(tmp)){path.push_back(tmp);dfs(i+1,s);path.pop_back();}elsecontinue;}}vector<vector<string>> partition(string s) {dfs(0,s);return ans;}
};

这篇关于代码随想录打卡—day27—【回溯】— 回溯基础练习 4.15+4.16的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---