Javascript 无处不在的二分搜索

本文主要是介绍Javascript 无处不在的二分搜索，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

我们知道二分查找算法。二分查找是最容易正确的算法。我提出了一些我在二分搜索中收集的有趣问题。有一些关于二分搜索的请求。我请求您遵守准则：“我真诚地尝试解决问题并确保不存在极端情况”。阅读完每个问题后，最小化浏览器并尝试解决它。
问题陈述：给定一个由 N 个不同元素组成的排序数组，使用最少的比较次数在数组中找到一个键。（您认为二分搜索是在排序数组中搜索键的最佳选择吗？）无需太多理论，这里是典型的二分搜索算法。

// Javascript code to implement the approach

// Returns location of key, or -1 if not found
function BinarySearch(A, l, r, key) {
let m;

while (l < r) {
m = l + (r - l) / 2;

if (A[m] == key) // first comparison
return m;

if (A[m] < key) // second comparison
l = m + 1;
else
r = m - 1;
}

return -1;
}

// This code is contributed by gfgking

理论上，最坏情况下我们需要进行log N + 1次比较。如果我们观察的话，我们会在每次迭代中使用两次比较，除非最终成功匹配（如果有）。在实践中，比较将是昂贵的操作，它不仅仅是原始类型比较。尽量减少与理论极限的比较更为经济。请参阅下图，了解下一个实现中索引的初始化。

以下实现使用较少的比较次数。

// Invariant: A[l] <= key and A[r] > key
// Boundary: |r - l| = 1
// Input: A[l .... r-1]
function BinarySearch(A, l, r, key)
{
let m;

while( r - l > 1 )
{
m = l + (r-l)/2;

if( A[m] <= key )
l = m;
else
r = m;
}

if( A[l] == key )
return l;
if( A[r] == key )
return r;
else
return -1;
}

在 while 循环中，我们仅依赖于一次比较。搜索空间收敛到将l和r指向两个不同的连续元素。我们需要再进行一次比较来跟踪搜索状态。您可以查看示例测试用例 http://ideone.com/76bad0。（C++11 代码）。

问题陈述：给定一个由 N 个不同整数组成的数组，找到输入“key”的下限值。假设 A = {-1, 2, 3, 5, 6, 8, 9, 10} 且 key = 7，我们应该返回 6 作为结果。我们可以使用上面的优化实现来找到键的下限值。只要不变量成立，我们就不断地将左指针移到最右边。最终左指针指向小于或等于 key 的元素（根据定义下限值）。以下是可能的极端情况， —> 如果数组中的所有元素都小于 key，则左指针移动到最后一个元素。 —> 如果数组中的所有元素都大于 key，则为错误情况。 —> 如果数组中的所有元素都相等且 <= key，则这是我们实现的最坏情况输入。
这是示例：

// largest value <= key
// Invariant: A[l] <= key and A[r] > key
// Boundary: |r - l| = 1
// Input: A[l .... r-1]
// Precondition: A[l] <= key <= A[r]
function Floor(A, l, r, key){
let m;
while(r - l > 1){
m = l + parseInt((r-l)/2);
if(A[m] <= key) l = m;
else r = m;
}
return A[l];
}

// Initial call
function Floor(A, size, key)
{
// Add error checking if key < A[0]
if( key < A[0] )
return -1;

// Observe boundaries
return Floor(A, 0, size, key);
}

// THIS CODE IS CONTRIBUTED BY YASH AGARWAL(YASHAGAWRAL2852002)

您可以看到一些测试用例 http://ideone.com/z0Kx4a。

问题陈述：给定一个可能有重复元素的排序数组。查找log N时间内输入“key”出现的次数。这里的想法是使用二分搜索查找数组中最左边和最右边出现的键。我们可以修改底函数来跟踪最右边的出现和最左边的出现。
这是示例：

// Input: Indices Range [l ... r)
// Invariant: A[l] <= key and A[r] > key
function getRightPosition(A, l, r, key) {
while (r - l > 1) {
const m = l + Math.floor((r - l) / 2);
if (A[m] <= key) {
l = m;
} else {
r = m;
}
}
return l;
}

// Input: Indices Range (l ... r]
// Invariant: A[r] >= key and A[l] > key
function getLeftPosition(A, l, r, key) {
while (r - l > 1) {
const m = l + Math.floor((r - l) / 2);
if (A[m] >= key) {
r = m;
} else {
l = m;
}
}
return r;
}

function countOccurrences(A, size, key) {
// Observe boundary conditions
let left = getLeftPosition(A, -1, size - 1, key);
let right = getRightPosition(A, 0, size, key);

// What if the element doesn't exist in the array?
// The checks help to determine whether the element exists

if (A[left] === key && key === A[right]) {
return right - left + 1;
}
return 0;
}

// Example usage
const A = [1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 6];
const key = 4;
const size = A.length;
const occurrences = countOccurrences(A, size, key);
console.log(`The number of occurrences of ${key} is: ${occurrences}`);

示例代码 zn6R6a - Online C++0x Compiler & Debugging Tool - Ideone.com。

问题陈述： 给定一个由不同元素组成的排序数组，并且该数组在未知位置旋转。找到数组中的最小元素。我们可以在下图中看到示例输入数组的图示。

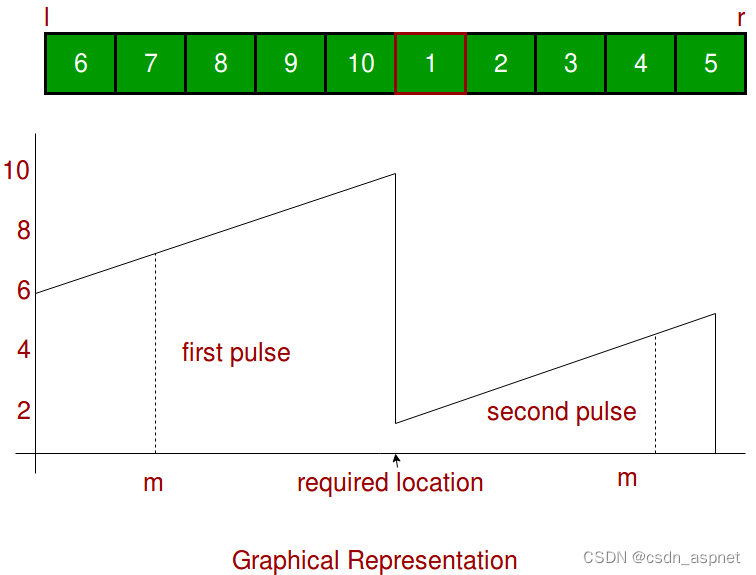
我们收敛搜索空间直到l和r 指向单个元素。如果中间位置落在第一个脉冲中，则不满足条件 A[m] < A[r]，我们将搜索空间收敛到 A[m+1 … r]。如果中间位置落在第二个脉冲中，则满足条件 A[m] < A[r]，我们将搜索空间收敛到 A[1 … m]。在每次迭代中，我们都会检查搜索空间大小，如果它是 1，我们就完成了。
下面给出的是算法的实现。你能想出不同的实施方案吗？