本文主要是介绍【单调栈】力扣85.最大矩形,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
好久没更新了 ~ 我又回来啦!
两个好消息:
- 我考上研了,收到拟录取通知啦!
- 开放 留言功能 了,小伙伴对于内容有什么疑问可以在文章底部评论,看到之后会及时回复大家的!
前面更新过的算法,二叉树递归、动态规划、单调栈 小伙伴们学的怎么样了?
今天我们继续更新 单调栈 的题目,一起学习吧!
(还没看过前几篇介绍的小伙伴赶快关注,在 「单调栈」 合集里查看哦!)
力扣85.最大矩形
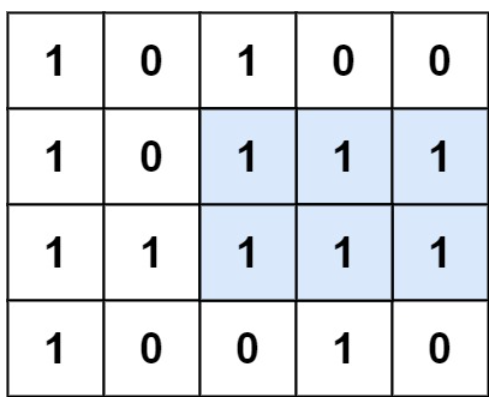
给定一个仅包含 0 和 1 、大小为 rows * cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1 :
输入: matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出: 6
解释: 如图
思路分析
上道题目我们解决了柱状图的问题,我们来思考一下,是否能够将此题也转化为与柱状图类似的思路呢?当然可以。
来看下面这个对比图,是不是很类似呀:
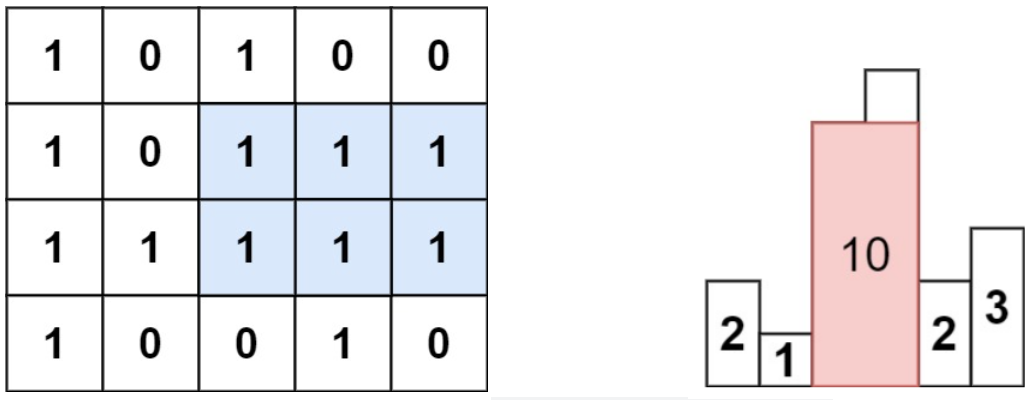
阴影部分都是矩形。
因此,我们可以将矩阵中每列 1 的个数看做是右侧的柱状图的高度,这样两道题目就 划归 到一起了。
关键点: 以某一行作为底边,看必须以这一行为底的矩阵每列的最大高度是多少。从而转化为 上道题目。
所以,我们的首要任务是,统计出以该行为底的高度是多少,之后再调用上道题的代码求解出矩形面积即可。
根据 上一篇 总结的经验,只需考虑在含有相同值时,最后一个相同元素是否能够将答案计算正确呢?答案是可以的!
这里就不再赘述了,不太懂的小伙伴可以去查看上一篇文章哦 ~
代码
public static int maximalRectangle(char[][] map) {if (map == null || map.length == 0 || map[0].length == 0) {return 0;}int maxArea = 0;int[] h = new int[map[0].length];for (int i = 0; i < map.length; i++) {for (int j = 0; j < map[0].length; j++) {h[j] = map[i][j] == '0' ? 0 : h[j] + 1;}// 调用上道题目的 求最大矩形的面积函数maxArea = Math.max(maxRecFromBottom(h),maxArea);}return maxArea;
}
这里的 maxRecFromBottom() 函数就是上篇文章的 largestRectangleArea1() 函数哦!一样的套路 ~
代码解释
这里采用了 压缩数组 的方式进行计算(这个思想在 动态规划专题 中也练习过哦~)。
一维数组 h[map[0].length] 用来存放当前所在行的信息:以当前行为底,第 j 列的高度为多少。
注意:
- 如果当前位置为 0 时,数组值归 0 。(当然不能以 0 为底啦)!
- 否则,上一行此位置的值 + 1,就是当前此位置 1 的最大的高度。
得到了柱状图的高度大小之后,就划归成了计算柱状图的最大面积了,直接套用 上道题的代码 即可~
~ 点赞 ~ 关注 ~ 星标 ~ 不迷路 ~!!!
关注回复「ACM紫书」获取 ACM 算法书籍~
记得转发哦!
这篇关于【单调栈】力扣85.最大矩形的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!