吴恩达深度学习笔记：深度学习的实践层面 (Practical aspects of Deep Learning)1.4-1.5

本文主要是介绍吴恩达深度学习笔记：深度学习的实践层面 (Practical aspects of Deep Learning)1.4-1.5，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第一门课：第二门课改善深层神经网络：超参数调试、正则化以及优化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)

第一周：深度学习的实践层面 (Practical aspects of Deep Learning)

1.4 正则化（Regularization）

深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。

下面我们就来讲讲正则化的作用原理。

我们用逻辑回归来实现这些设想，求成本函数𝐽的最小值，它是我们定义的成本函数，参数包含一些训练数据和不同数据中个体预测的损失，w和b是逻辑回归的两个参数，w是一个多维度参数矢量，b是一个实数。在逻辑回归函数中加入正则化，只需添加参数 λ，也就是正则化参数，一会儿再详细讲。

$\frac{λ}{2m}$ 乘以w范数的平方，w欧几里德范数的平方等于 $w_j$ （j 值从 1 到n_x）平方的和，也可表示为 $w^Tw$ ，也就是向量参数w 的欧几里德范数（2 范数）的平方，此方法称为𝐿2正则化。因为这里用了欧几里德法线，被称为向量参数𝑤的𝐿2范数。

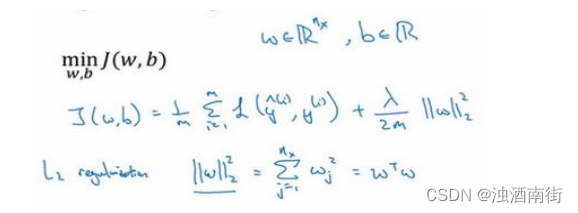
在这里插入图片描述
为什么只正则化参数𝑤？为什么不再加上参数 𝑏 呢？因为𝑤通常是一个高维参数矢量，已经可以表达高偏差问题，𝑤可能包含有很多参数，
我们不可能拟合所有参数，而𝑏只是单个数字，所以𝑤几乎涵盖所有参数，而不是𝑏，如果加了参数𝑏，其实也没太大影响，因为𝑏只是众多参数中的一个，所以我通常省略不计，如果你想加上这个参数，完全没问题。

𝐿2正则化是最常见的正则化类型，你们可能听说过𝐿1正则化，𝐿1正则化，加的不是𝐿2范数，而是正则项 $\frac{λ}{m}$ 乘以 $\sum_{j=1}^{nx}{|x|}$ ， $\sum_{j=1}^{nx}{|x|}$ 也被称为参数𝑤向量的𝐿1范数，无论分母是𝑚还是2𝑚，它都是一个比例常量。

如果用的是𝐿1正则化，𝑤最终会是稀疏的，也就是说𝑤向量中有很多 0，有人说这样有利于压缩模型，因为集合中参数均为 0，存储模型所占用的内存更少。实际上，虽然𝐿1正则化使模型变得稀疏，却没有降低太多存储内存，所以我认为这并不是𝐿1正则化的目的，至少不是为了压缩模型，人们在训练网络时，越来越倾向于使用𝐿2正则化。

我们来看最后一个细节，𝜆是正则化参数，我们通常使用验证集或交叉验证集来配置这个参数，尝试各种各样的数据，寻找最好的参数，我们要考虑训练集之间的权衡，把参数设置为较小值，这样可以避免过拟合，所以 λ 是另外一个需要调整的超级参数，顺便说一下，为了方便写代码，在 Python 编程语言中，𝜆是一个保留字段，编写代码时，我们写成𝑙𝑎𝑚𝑏𝑑，以免与 Python 中的保留字段冲突，这就是在逻辑回归函数中实现𝐿2正则化的过程，如何在神经网络中实现𝐿2正则化呢？

神经网络含有一个成本函数，该函数包含 $W^{[1]}，b^{[1]}$ 到 $W^{[l]}，b^{[l]}$ 所有参数，字母𝐿是神经网络所含的层数，因此成本函数等于𝑚个训练样本损失函数的总和乘以 $\frac{1}{m}$ ，正则项为 $\frac{λ}{2m}\sum_{1}^L{||W^{[l]}||^2}$ ，我们称 $W^{[l]}||^2$ 为范数平方，这个矩阵范数 $W^{[l]}||^2$ （即平方范数），被定义为矩阵中所有元素的平方求和。
在这里插入图片描述
我们看下求和公式的具体参数，第一个求和符号其值i从 1 到 $n^{[l−1]}$ ，第二个其J值从 1 到 $n^{[l]}$ ，因为𝑊是一个 $n^{[l]} x n^{[l−1]}$ 的多维矩阵， $n^{[l]}$ 表示𝑙 层单元的数量， $n{[l−1]}$ 表示第𝑙 − 1层隐藏单元的数量。
在这里插入图片描述
该矩阵范数被称作“弗罗贝尼乌斯范数”，用下标𝐹标注，鉴于线性代数中一些神秘晦涩的原因，我们不称之为“矩阵𝐿2范数”，而称它为“弗罗贝尼乌斯范数”，矩阵𝐿2范数听起来更自然，但鉴于一些大家无须知道的特殊原因，按照惯例，我们称之为“弗罗贝尼乌斯范数”，它表示一个矩阵中所有元素的平方和。

该如何使用该范数实现梯度下降呢？
用 backprop 计算出𝑑𝑊的值，backprop 会给出𝐽对𝑊的偏导数，实际上是𝑊[𝑙]，把𝑊[𝑙]替换为𝑊[𝑙]减去学习率乘以𝑑𝑊。

这就是之前我们额外增加的正则化项，既然已经增加了这个正则项，现在我们要做的就是给dW加上这一项 $\frac{λ}{m}W^{[l]}$ ，然后计算这个更新项，使用新定义的 $dW^{[l]}$ ，它的定义含有相关参数代价函数导数和，以及最后添加的额外正则项，这也是𝐿2正则化有时被称为“权重衰减”的原因。
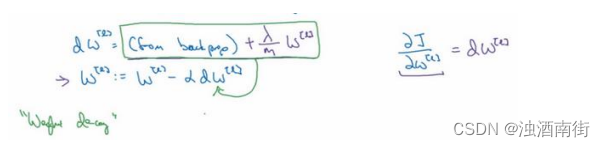
在这里插入图片描述
我们用 $dW^{[l]}$ 的定义替换此处的 $dW^{[l]}$ ，可以看到， $W^{[l]}$ 的定义被更新为 $W^{[l]}$ 减去学习率𝑎 乘以 backprop 再加上 $\frac{λ}{m}W^{[l]}$ 。

该正则项说明，不论 $W [l]$ 是什么，我们都试图让它变得更小，实际上，相当于我们给矩阵 W 乘以(1 − 𝑎 $\frac{λ}{m}$ )倍的权重，矩阵𝑊减去𝛼 $\frac{λ}{m}$ 倍的它，也就是用这个系数(1 − $\frac{λ}{m}$ )乘以矩阵𝑊，该系数小于 1，因此𝐿2范数正则化也被称为“权重衰减”，因为它就像一般的梯度下降，𝑊被更新为少了𝑎乘以 backprop 输出的最初梯度值，同时𝑊也乘以了这个系数，这个系数小于 1，因此𝐿2正则化也被称为“权重衰减”。