本文主要是介绍状态压缩DP题单,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
P1433 吃奶酪(最短路)
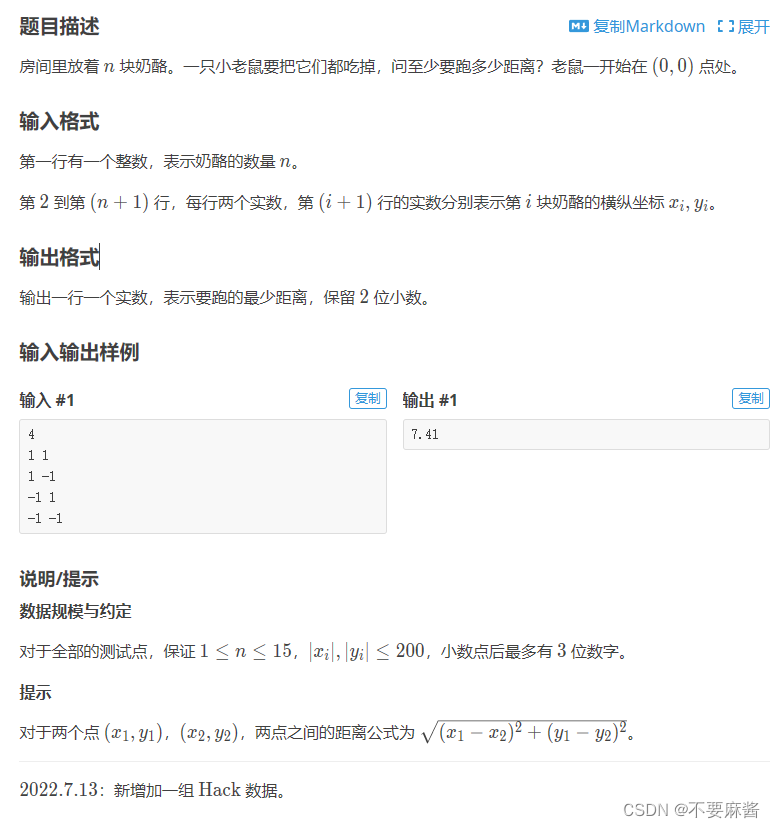
dp(i, s) 表示从 i 出发经过的点的记录为 s 的路线距离最小值
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 20;
signed main()
{ int n; cin >> n;vector<double>x(n + 1), y(n + 1);vector<vector<double>> dp(n + 1, vector<double>(1 << (n + 1), 2e9));x[0] = 0, y[0] = 0;auto dis = [&](int i, int j) -> double{return sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));};for(int i = 1; i <= n; i ++){cin >> x[i] >> y[i];
// dp[i][1 << (i - 1)] = 0;}dp[0][1] = 0;for(int s = 1; s < (1 << (n + 1)); s ++){for(int i = 0; i <= n; i ++){if((s & (1 << (i))) == 0) continue;for(int j = 0; j <= n; j ++){if(i == j) continue;if((s & (1 << (j))) == 0) {continue;}
// cout << s << " " << i << " " << j << '\n';dp[i][s] = min(dp[i][s], dp[j][s - (1 << (i))] + dis(i, j)); }}}double ans = -1;for(int i = 1; i <= n; i ++){double s = dp[i][(1 << (n + 1)) -1];if(ans==-1||ans>s) ans=s;}cout << fixed << setprecision(2) << ans << '\n';
}
P8733 [蓝桥杯 2020 国 C] 补给(floyd)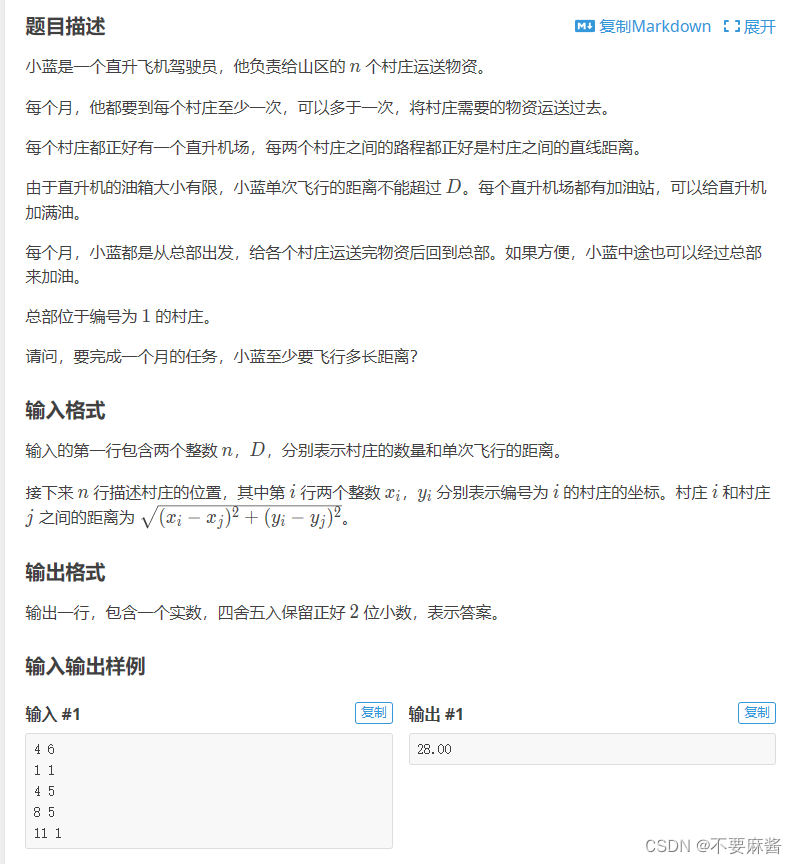
dp(i, s) 表示到达 i ,经过的点的记录为 s 的路线距离最小值
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 20;
signed main()
{ int n, D; cin >> n >> D;vector<double>x(n + 1), y(n + 1);vector<vector<double>> dp(n + 1, vector<double>((1 << n) + 10, 2e9)), f(n + 1, vector<double>(n + 1, 2e9));auto dis = [&](int i, int j) -> double{return sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));};for(int i = 0; i < n; i ++) cin >> x[i] >> y[i];for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++){double now = dis(i, j);if(now <= D) f[i][j] = now;}for(int k = 0; k < n; k ++)for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)f[i][j] = min(f[i][k] + f[k][j], f[i][j]);dp[0][1] = 0;for(int s = 1; s < (1 << n); s ++){for(int i = 0; i < n; i ++){if((s & (1 << i)) == 0) continue;for(int j = 0; j < n; j ++){ if(i == j) continue;if((s & (1 << j)) == 0) continue;dp[i][s] = min(dp[i][s], dp[j][s - (1 << i)] + f[i][j]);
// cout << i << " " << j << " " << f[i][j] << '\n';}}}double ans = 1e9;for(int i = 0; i < n; i ++){
// cout << i << " " << (1 << (n - 1)) << " " << dp[i][1 << (n - 1)] << '\n';double now = f[0][i] + dp[i][(1 << n) - 1];ans = min(ans, now);}cout << fixed << setprecision(2) << ans << '\n';
}P7859 [COCI2015-2016#2] GEPPETTO(简单枚举状态)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 4e5 + 10;
typedef long long ll;
int a[25][25];
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n, m; cin >> n >> m;for(int i = 1; i <= m; i ++){int x, y; cin >> x >> y;a[x][y] = a[y][x] = 1;}int ans = 1;for(int s = 1; s < (1 << n); s ++){int f = 0;for(int i = 1; i <= n; i ++){if((s & (1 << (i - 1))) == 0) continue; for(int j = i + 1; j <= n; j ++){if((s & (1 << (j - 1))) == 0) continue;if(a[i][j] || a[j][i]) {f = 1;
// cout << s << " " << i << " " << (s & (1 << (i - 1))) << " " << j << " "<< (s & (1 << (j - 1))) << '\n'; break;}}if(f) break;}
// cout << s << ' ' << f << '\n';if(!f) ans ++;}cout << ans << '\n';
}P8687 [蓝桥杯 2019 省 A] 糖果

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 20;
/*
1 3 3
1 2 3
*/
signed main()
{ int n, m, k; cin >> n >> m >> k;vector<int>dp(1 << 21, -1), a(105);for(int i = 1; i <= n; i ++) {int s = 0;for(int j = 1; j <= k; j ++){int x; cin >> x;x --;s |= (1 << x);}
// s |= (1 << x), s |= (1 << y), s |= (1 << z);
// int s = (1 << x) + (1 << y) + (1 << z);a[i] = s;}dp[0] = 0;for(int s = 0; s < (1 << m); s ++){if(dp[s] == -1) continue;for(int i = 1; i <= n; i ++){if(dp[s | a[i]] == -1 || dp[s] + 1 < dp[s | a[i]]){dp[s | a[i]] = dp[s] + 1;
// cout << s << " " << i << " " << a[i] << ' ' << dp[s | a[i]] << '\n';}}}cout << dp[(1 << m) - 1] << '\n';
}[ABC332E] Lucky bag(SOS DP)
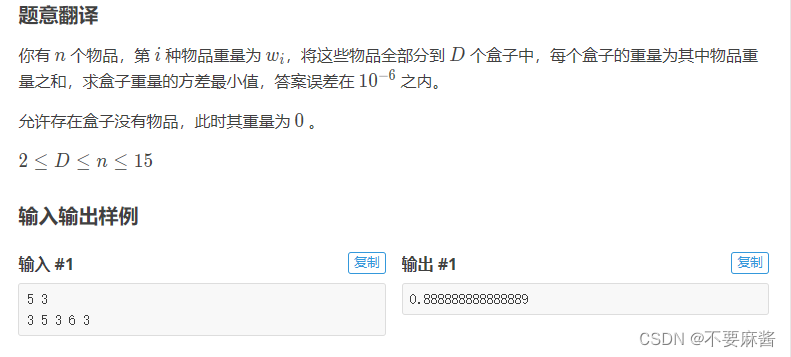
dp(s, i) 表示状态为 s 装入 i 个背包的最小值。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 25;
signed main()
{ ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);int n, d; cin >> n >> d;vector<double>a(n + 1);vector<vector<double>>dp(1 << n, vector<double>(d + 1, 1e18));double sum = 0;for(int i = 0; i < n; i ++){cin >> a[i];
// cout << a[i] << ' ';sum += a[i];}double ave = sum / d;
// cout << ave << '\n';for(int s = 0; s < (1 << n); s ++){double res = 0;for(int j = 0; j < n; j ++) if((1 << j) & s) res += a[j];dp[s][1] = (res - ave) * (res - ave);}for(int i = 2; i <= d; i ++){for(int s = 0; s < (1 << n); s ++){for(int t = s; t > 0; t = (t - 1) & s){dp[s][i] = min(dp[s][i], dp[t][i - 1] + dp[s ^ t][1]);
// cout << s << " " << i << '\n';}} }cout << fixed << setprecision(15) << dp[(1 << n) - 1][d] / d << '\n';
}彩色路径(最短路/边数限制+折半存储)
CCF-CSP认证考试 202312-5 彩色路径 20/50/100分题解_ccf彩色路径-CSDN博客
这篇关于状态压缩DP题单的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






