本文主要是介绍最小二乘法(Least square method),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最小二乘法是在线性回归模型最小化均方误差时使用,其实就是对误差函数求导数,然后让其等于0 ,然后解出使得误差最小。本篇文章讲解最小二乘法。
首先声明,此篇的内容是来自"马同学高等数学"微信公众号的内容。
目录
1、日用而不知
2、最小二乘法
3、推广
4、最小二乘法与正态分布
参考文献:
1、日用而不知
来看一个生活中的例子。比如说,有五把尺子:

用它们来分别测量一线段的长度,得到的数值分别为(颜色指不同的尺子):

之所以出现不同的值可能因为:
-
不同厂家的尺子的生产精度不同
-
尺子材质不同,热胀冷缩不一样
-
测量的时候心情起伏不定
-
......
总之就是有误差,这种情况下,一般取平均值来作为线段的长度:
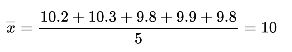
日常中就是这么使用的。可是作为很事'er的数学爱好者,自然要想下:
-
这样做有道理吗?
-
用调和平均数行不行?
-
用中位数行不行?
-
用几何平均数行不行?
2、最小二乘法
换一种思路来思考刚才的问题。首先,把测试得到的值画在笛卡尔坐标系中,分别记作 :

其次,把要猜测的线段长度的真实值用平行于横轴的直线来表示(因为是猜测的,所以用虚线来画),记作 :

每个点都向 做垂线,垂线的长度就是
,也可以理解为测量值和真实值之间的误差:

因为误差是长度,还要取绝对值,计算起来麻烦,就干脆用平方来代表误差:
![]()
误差的平方和就是( 代表误差):
![]()
因为 是猜测的,所以可以不断变换:误差的平方和
![]() 也在不断变化的。法国数学家,阿德里安-马里·勒让德(1752-1833)提出让总的误差的平方最小的
也在不断变化的。法国数学家,阿德里安-马里·勒让德(1752-1833)提出让总的误差的平方最小的 就是真值,这是基于,如果误差是随机的,应该围绕真值上下波动,勒让德的想法变成代数式就是:
![]()
这是一个二次函数,对其求导,导数为0的时候取得最小值:
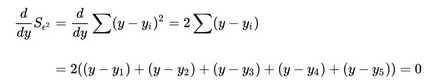
进而:
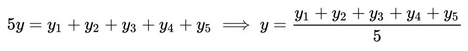
正好是算术平均数。原来算术平均数可以让误差最小啊,这下看来选用它显得讲道理了。以下这种方法:
![]()
就是最小二乘法,所谓“二乘”就是平方的意思。
3、推广
算术平均数只是最小二乘法的特例,适用范围比较狭窄。而最小二乘法用途就广泛。比如温度与冰淇淋的销量:
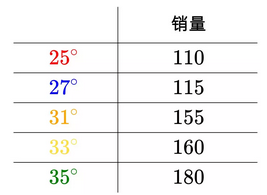
看上去像是某种线性关系:

可以假设这种线性关系为:![]() ,通过最小二乘法的思想:
,通过最小二乘法的思想:

上图的 分别为:
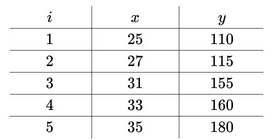
总误差的平方为:
![]()
不同的 会导致不同的
,根据多元微积分的知识,当:
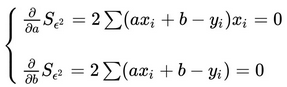
这个时候 , 取最小值。对于
而言,上述方程组为线性方程组,用之前的数据解出来:
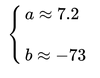
也就是这根直线:

其实,还可以假设:![]()
在这个假设下,可以根据最小二乘法,算出 ,得到下面这根红色的二次曲线:

同一组数据,选择不同的 ,通过最小二乘法可以得到不一样的拟合曲线:

从上图可以看到,多项式的幂次越高,其对数据的拟合程度越高,那么是不是我们就应该选择幂次尽量高的
呢,显然不是的,在机器学习中,这会产生过拟合现象,也就是说多项式能够完美的拟合训练集的数据,但是它的完美仅仅是相对于一直的这些数据而言的,如果输入新的测试数据,它反而不能较好的对新输入的数据进行拟合。其实在上图中,我们完全可以选择一次多项式作为拟合函数,虽然它相对于其他比它幂次更高的拟合程度并不高,但是其大致能拟合离散的数据点。根据奥卡姆剃刀原理,我们选择一次多项式作为拟合函数是最合适的。
4、最小二乘法与正态分布
我们对勒让德的猜测,即最小二乘法,仍然抱有怀疑,万一这个猜测是错误的怎么办?数学王子高斯(1777-1855)也像我们一样心存怀疑。高斯换了一个思考框架,通过概率统计那一套来思考。让我们回到最初测量线段长度的问题。高斯想,通过测量得到了这些值:
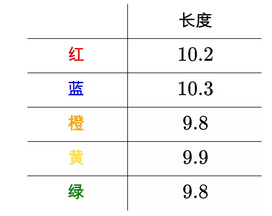
每次的测量值 都和线段长度的真值
之间存在一个误差:
,这些误差最终会形成一个概率分布,只是现在不知道误差的概率分布是什么。假设概率密度函数为:
再假设一个联合概率,这样方便把所有的测量数据利用起来:
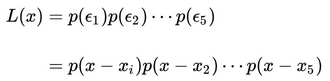
把 作为变量的时候,上面就是似然函数了。
的图像可能是这样的:

根据最大似然估计的思想,联合概率最大的最应该出现(既然都出现了,而我又不是“天选之子”,那么自然不会是发生了小概率事件),也就是应该取到下面这点:

当下面这个式子成立时,取得最大值:![]() , 然后高斯想,最小二乘法给出的答案是:
, 然后高斯想,最小二乘法给出的答案是:
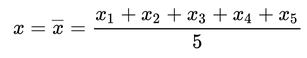
如果最小二乘法是对的,那么 时应该取得最大值,即:
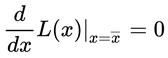
好,现在可以来解这个微分方程了。最终得到:
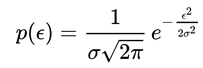
这是什么?这就是正态分布啊。并且这还是一个充要条件:
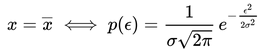
也就是说,如果误差的分布是正态分布,那么最小二乘法得到的就是最有可能的值。
那么误差的分布是正态分布吗?
如果误差是由于随机的、无数的、独立的、多个因素造成的,比如之前提到的:
-
不同厂家的尺子的生产精度不同
-
尺子材质不同,热胀冷缩不一样
-
测量的时候心情起伏不定
-
......
那么根据中心极限定理,误差的分布就应该是正态分布。虽然勒让德提出了最小二乘法(高斯说他最早提出最小二乘法,只是没有发表),但是高斯的努力,才真正奠定了最小二乘法的重要地位。
参考文献:
如何理解最小二乘法? https://mp.weixin.qq.com/s/4e9ZiiGIOWx_ZUGjzgavWw
这篇关于最小二乘法(Least square method)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



