单源最短路径问题--Dijkstra算法

本文主要是介绍单源最短路径问题--Dijkstra算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Dijkstra算法实现

1.算法过程
2.代码实现过程
- 2.1朴素Dijkstra实现
- 2.2朴素Dijkstra实现

1.算法过程

Dijkstra算法是图论中用来解决单元最短路径的算法，我们通过将点划分成为两个部分，一个是已经确定了源点到达此处最短路径的点，另外一个部分是还不确定最短路径的点。我们每次每一次选择状态图中最短路，将最短路端点A标记成为已经确定最短路径的点集，接着看看是否有通过A这个最短路径可以有一条更短的路到达未确定的点，如果有的话，就更新源点到达这个点路径的最短信息。接着重复找到最短的路径加入，重复上面步骤，指导所有点都找完。确切算法描述过程如下：
在这里插入图片描述在算法实现过程中，每次选择最短路径和更新路径信息是耗时较多的地方，所以我们选择最短路的时候，是否通过堆来优化，将Dijkstra算法划分成为了朴素Dijkstra（就是没次选择最短路加入的时候，需要将所有路径长度遍历一次）和堆优化的Dijkstra。

2.代码实现过程

这里以leecode中题目为例子来讲述Dijkstra的实现过程，代码是参考灵茶山艾府的题解
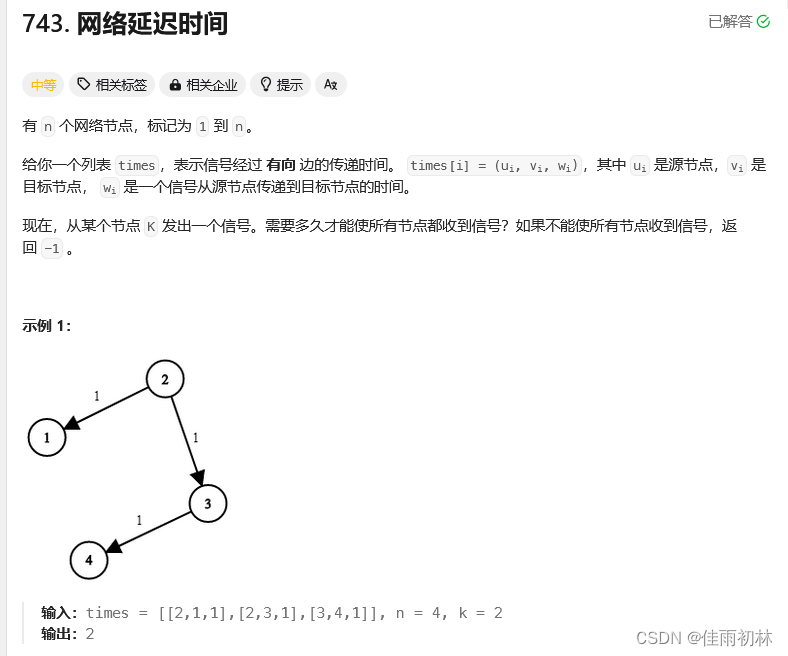
在这里插入图片描述

2.1朴素Dijkstra实现

注意朴素Dijkstra的实现利用的图的存储结构是邻接矩阵

class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<vector<int>> g(n, vector<int>(n, INT_MAX / 2));//邻接矩阵存储for(auto &t : times){g[t[0] - 1][t[1] - 1] = t[2];}//dis用来存储单元的最短的路径；done用来标记是否已经确定了最短路径vector<int> dis(n, INT_MAX / 2), done(n);//顶点k作为源点dis[k - 1] = 0;while(true){int x = -1;for(int i = 0; i < n; i++){//用来确定最短路径：x是用来标记确定最短路径的另一端的点if(!done[i] && (x < 0 || dis[i] < dis[x])){x = i;}}//表示已经确定了所有点的最短路径if(x < 0) return ranges::max(dis);//有节点无法到达if(dis[x] == INT_MAX / 2) return -1;//最短路长度已经确定，无法变得更小done[x] = true;//确定源点到达x最短路径之后，需要判断是否更新源点到达x相连点的路径长度for(int y = 0; y < n; y++){//更新x的邻居的最短路dis[y] = min(dis[y], dis[x] + g[x][y]);}}}
};

2.2朴素Dijkstra实现

堆优化实现的过程中，需要去把这个判断语句的作用给弄明白

if(dx > dis[x]) continue;

这个因为我们利用堆实现的过程中，我们确定了最短路径的点加入之后，我们的更新路径的信息过程不会直接去把堆中的信息给修改，而是直接再插入一个更短的路径信息上去。
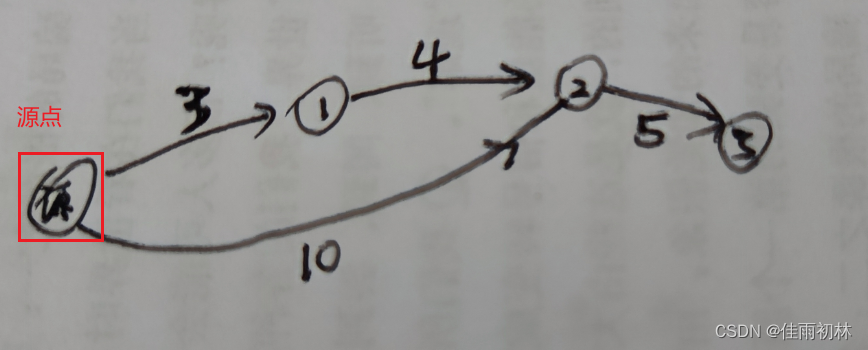
例如下图：我们源点确定了之后，会将源点相连的点1和点2的路径信息更新为3和10（其余点为无穷），
但是接下我们堆中的最短路径长度3（源点到达点1），此时通过点1我们发现源点到达点2的距离可以有一条比长度10更短的路径长度7，但是此时我们不会直接去将堆中的10给删除，而是插入一个7。同时记住一下到达点2的路可以用7就到达，所以之后我们堆弹出10的时候，我们不会拿着10（脏数据）去更新点2的最短路径。
在这里插入图片描述

class Solution {
public://邻接表适合稀疏图int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<vector<pair<int, int>>> g(n);//邻接表for(auto &t :times){//x -> y: 把y和x到y距离打包成pair拉链到点x下面g[t[0] - 1].emplace_back(t[1] - 1, t[2]);}//存储最短路径vector<int> dis(n, INT_MAX);//从源点k出发dis[k - 1] = 0;//定义一个最小堆，维护源点到达其他顶点未选择路径的最短路（第二个参数指名了底层实现的堆的数据结构）priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;//pq中的pair为：<distance, point>pq.emplace(0, k - 1);while(!pq.empty()){auto [dx, x] = pq.top();pq.pop();//x之前出堆过（对于同一个 x，入堆的 dis[x] 只会越来越小，那么首先弹出的就是最小的 dis[x]，//后面弹出的 dx 必定比 dis[x] 大。既然首先弹出的是最小的，所以首次弹出的 dx 等于 dis[x]）if(dx > dis[x]) continue;for(auto &[y, d] :g[x]){int new_dis = dx + d;if(new_dis < dis[y]){//跟新x的邻居的最短路dis[y] = new_dis;pq.emplace(new_dis, y);}}}int mx = ranges::max(dis);return mx < INT_MAX ? mx : -1;}
};