本文主要是介绍【机器学习300问】71、神经网络中前向传播和反向传播是什么?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我之前写了一篇有关计算图如何帮助人们理解反向传播的文章,那为什么我还要写这篇文章呢?是因为我又学习了一个新的方法来可视化前向传播和反向传播,我想把两种方法总结在一起,方便我自己后续的复习。对了顺便附上往期文章的链接方便回顾:
【机器学习300问】59、计算图是如何帮助人们理解反向传播的?![]() http://t.csdnimg.cn/QMYZt
http://t.csdnimg.cn/QMYZt
一、用计算图来理解
再用小孩儿做数学题的例子来为大家介绍什么是前向传播(又叫正向传播),什么是反向传播。假设你在教一个小孩儿,计算
。
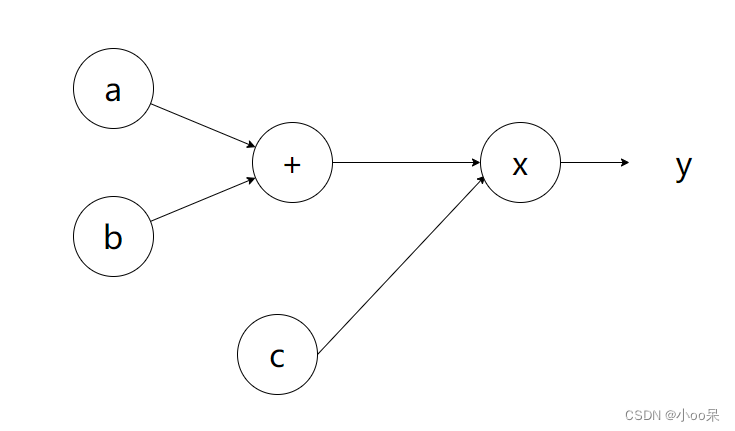
(1)前向传播
就像是小孩按照步骤一步步计算题目。比如说他要计算 (a+b) × c,他先算出 a+b 的结果,然后再把这个结果乘以 c 得到最后的答案。
前向传播是神经网络中从输入层到输出层的计算过程。在神经网络中,输入层接收原始数据,然后通过隐藏层的处理,最终由输出层产生预测结果。每个神经元都会根据前一层神经元的输出和自身的权重进行计算,然后将结果传递给下一层。
(2)损失函数
相当于你用来判断小孩答案对错的标准,本质是个衡量错误程度的“分数”。如果他的答案离正确答案差很多,那么这个分数就会很高,表示他错的很离谱。反之,若他的损失分数很小,说明他的答案很接近正确答案。
损失函数是用来衡量神经网络预测结果与实际结果之间差距的指标。损失函数越小,说明神经网络的预测结果越接近实际结果。在训练过程中,我们的目标就是最小化损失函数。
(3)反向传播
反向传播类似你指导小孩如何改正错误的过程。假设他最后的答案错了,你会告诉他:“你计算的最后一步有问题,你需要知道是因为 c 值没乘对还是前面 a+b 的结果就不对。”于是你从最后一个步骤开始,告诉小孩每一步对他最后答案的影响有多大(也就是计算梯度),这样他才能有针对性地调整自己的计算步骤,以便下次做得更好。
反向传播是神经网络中根据损失函数的梯度信息调整权重的过程。在前向传播得到预测结果并计算损失函数后,我们需要知道每个权重对损失函数的影响程度,也就是梯度。通过反向传播算法,我们可以从输出层开始,逐层计算每个神经元的梯度,并根据梯度信息更新权重。
二、用神经网络块来理解
让我们首先来画一个神经网络:
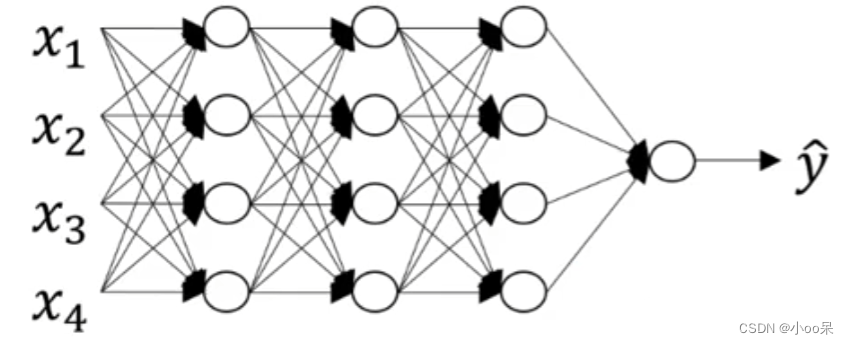
我先用语言来描述一下这个神经网络,上图是一个四层神经网络,有三个隐藏层。我们用来表示隐藏层总个数,显然
。输入层的索引为0,故三个隐藏层的神经元个数
分别表示为
。而输入层的特征数表示为
。而每层都用
来表示激活函数输出的结果。输入激活函数中权重和偏置表示为:
(1)神经网络块

在第层你有参数
和
,正向传播里有输入的激活函数,输入是前一层
,输出是
,我们之前讲过
,,那么上图就是可视化展示出如何从
输入
走到输出
的。之后你就可以把
的值缓存起来,因为缓存的
对以后的正向反向传播的步骤非常有用。
然后是反向步骤或者说反向传播步骤,同样也是第层的计算,你需要实现一个函数输入为
,输出
的函数。一个小细节需要注意,输入在这里其实是
以及所缓存的
值,之前计算好的
值,除了输出的
值以外,还需要输出你需要的梯度
和
,这是为了实现梯度下降。
(2)前向传播

在正向传播过程中,“传播”的是信号数据(就是你通过节点式子算出来的值)。
(3)反向传播
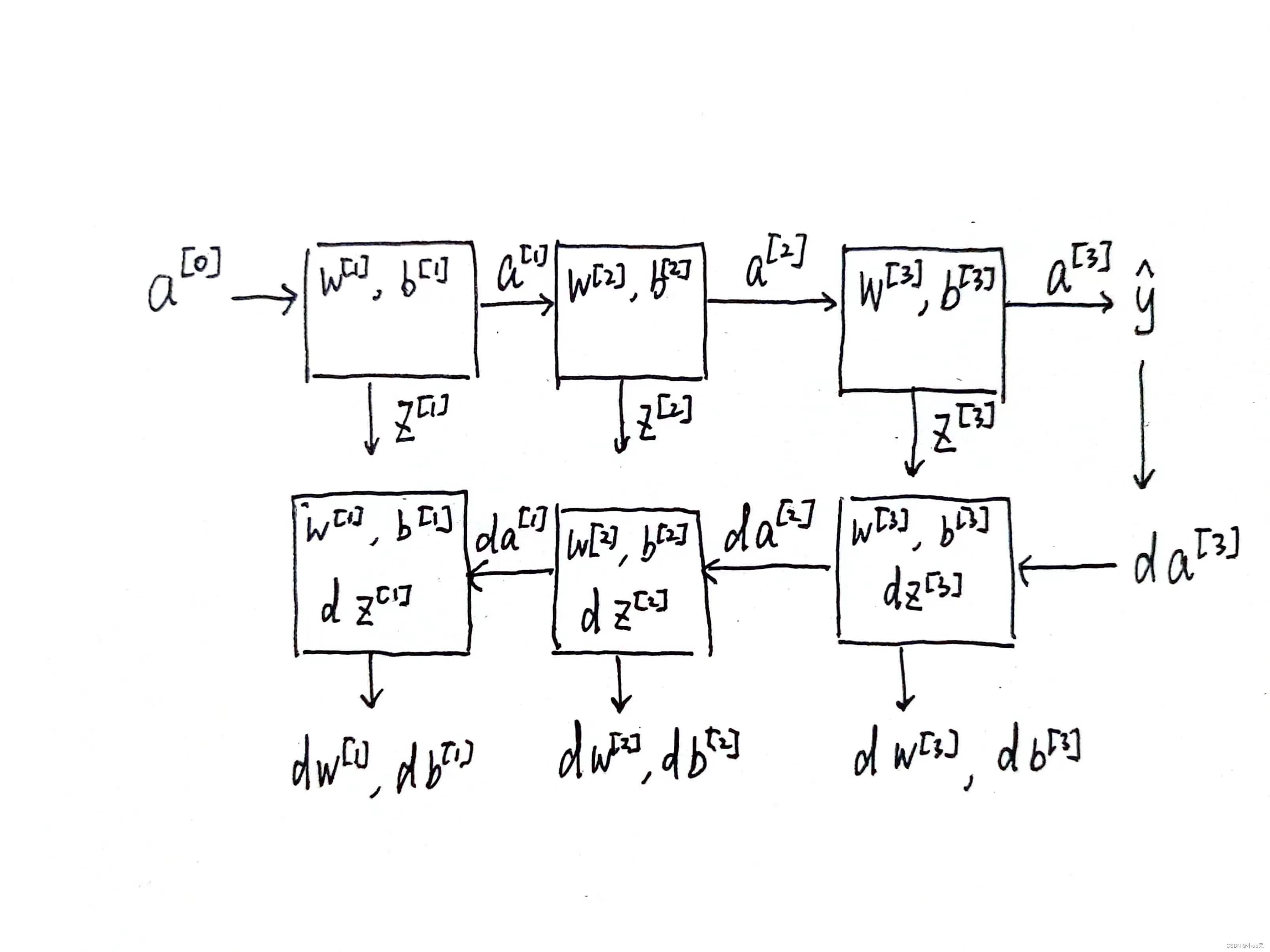
通过完整的神经网络计算块,可以清晰直观的感受前向传播和反向传播参数和参数的梯度是如何在各层中传递的。 反向传播,“传播”的是误差信号在神经网络中的梯度(梯度就是指导参数该怎么变的变化率)。
这篇关于【机器学习300问】71、神经网络中前向传播和反向传播是什么?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








