2016NOIP普及组真题 4. 魔法阵

本文主要是介绍2016NOIP普及组真题 4. 魔法阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

线上OJ：

一本通：http://ybt.ssoier.cn:8088/problem_show.php?pid=1976

本题作为第四题，想拿满分有难度。但是暴力拿些分还是做得到的。
满分需要用 前缀和 来化简for循环。

核心语句：

$ x_a < x_b < x_c < x_d $ ①
$ x_b - x_a = 2(x_d - x_c) $ ②
$ x_b - x_a < (x_c - x_b)/3 $ ③

核心思想：

由于魔法值 n 不超过 15000，但魔法球的数量 m 可达到40000。
所以选择反向枚举答案：即对所有的魔法值进行枚举（先找出 n 范围内所有符合上述三个公式的魔法组合数字），这样可避免对魔法球进行排序。

另外，由于魔法球的魔法数值可能相同，所以在计算每一个数字的出现次数时，要考虑其他数字的组合出现情况。如下图所示：

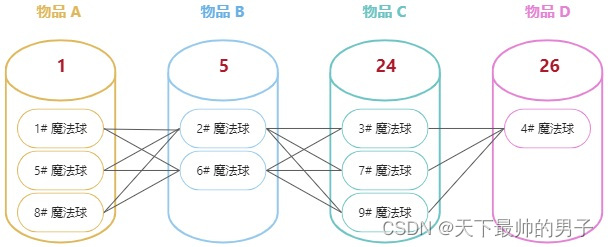
在这里插入图片描述

上图中，1# 魔法球在物品A中出现的次数为6次，分别为：
1#，2#，3#，4#
1#，2#，7#，4#
1#，2#，9#，4#
1#，6#，3#，4#
1#，6#，7#，4#
1#，6#，9#，4#

上图中，2# 魔法球在物品B中出现的次数为9次，分别为：
1#，2#，3#，4#
1#，2#，7#，4#
1#，2#，9#，4#
5#，2#，3#，4#
5#，2#，7#，4#
5#，2#，9#，4#
8#，2#，3#，4#
8#，2#，7#，4#
8#，2#，9#，4#

所以每一个魔法球在某个位置出现的 次数 = 剩余位置魔法球数量的乘积（组合思想）

题解代码：

解法一、

#include <bits/stdc++.h>
#define MAXN 40005
using namespace std;struct Node
{int val, id;	// 存储节点的值和 id。 id用于最终的输出
};
Node node[MAXN];int n, m;	// m 个魔法物； 魔法值不超过 n
int ge[MAXN]; // 记录val为i的魔法物的个数。用于计算组合
int cnta[MAXN], cntb[MAXN], cntc[MAXN], cntd[MAXN];		// cnta[i]表示val为i的魔法物在A位置出现的次数
// cntb[i]表示val为i的魔法物在B位置出现的次数, cntc[i]表示val为i的魔法物在C位置出现的次数 等// 暴力枚举 70% 分数。
int main()
{scanf("%d%d",&n, &m);int x;for(int i = 1; i <= m; i++){scanf("%d", &x);node[i].val = x;node[i].id = i;ge[x]++;  // 统计魔法值为x的物品个数}// 反向枚举结果：对所有的魔法值进行枚举（即先找出 n 范围内所有符合要求的魔法组合数字），可避免排序。// 不是对每个魔法球的魔法值进行枚举（每一轮都是枚举40000和枚举15000的区别）for(int ai = 1; ai <= n - 3; ai++)for(int bi = ai + 1; bi <= n - 2; bi++)for(int ci = bi + 1; ci <= n - 1; ci++)for(int di = ci + 1; di <= n; di++)if( ( (bi-ai) == 2*(di-ci) ) && ( 3*(bi-ai) < (ci-bi) ) ){	// 如果找到一组符合要求的魔法值，则更新各数字在对应位置出现的次数// 考虑到不同的魔法球会有相同的魔法值，所以在作组合计算时对其余位置作数量的乘法cnta[ai] += ge[bi] * ge[ci] * ge[di];cntb[bi] += ge[ai] * ge[ci] * ge[di];cntc[ci] += ge[ai] * ge[bi] * ge[di];cntd[di] += ge[ai] * ge[bi] * ge[ci];break;	// 1个abc只能对应1个d，如果找到了，直接退出循环}for(int i = 1; i <= m; i++){int t = node[i].val;printf("%d %d %d %d\n",cnta[t], cntb[t], cntc[t], cntd[t]);}return 0;
}

以上暴力代码比较简单，只要注意 反向枚举，就可以在考场上快速拿到70%的分数。

解法二、优化区间

接下来对解法一进行优化。
把对公式③ $ x_b - x_a < (x_c - x_b)/3 $ 的利用，从条件判断改为直接赋值给ci的范围。
因为 $x_b-x_a < (x_c-x_b)/3$ ，移项后可得 $x_c > 4x_b-3x_a$ ，所以 $x_c$ 从 $4x_b-3x_a+1$ 开始取值。
所以 $c i = 4 * bi - 3 * ai + 1$ 。
同时，由于1个abc只能对应1个d，如果找到了符合条件的d，就退出最内层的循环。

#include <bits/stdc++.h>
#define MAXN 40005
using namespace std;struct Node
{int val, id;	// 存储节点的值和 id。 id用于最终的输出
};
Node node[MAXN];int n, m;	// m 个魔法物； 魔法值不超过 n
int ge[MAXN]; // 记录val为i的魔法物的个数。用于计算组合
int cnta[MAXN], cntb[MAXN], cntc[MAXN], cntd[MAXN];		// cnta[i]表示val为i的魔法物在A位置出现的次数
// cntb[i]表示val为i的魔法物在B位置出现的次数, cntc[i]表示val为i的魔法物在C位置出现的次数 等// 暴力枚举 80% 分数。
int main()
{scanf("%d%d",&n, &m);int x;for(int i = 1; i <= m; i++){scanf("%d", &x);node[i].val = x;node[i].id = i;ge[x]++;  // 统计魔法值为x的物品个数}// 反向枚举结果：对所有的魔法值进行枚举（即先找出 n 范围内所有符合要求的魔法组合数字），可避免排序。// 不是对每个魔法球的魔法值进行枚举（每一轮都是枚举40000和枚举15000的区别）for(int ai = 1; ai <= n - 3; ai++)for(int bi = ai + 1; bi <= n - 2; bi++)for(int ci = 4 * bi - 3 * ai + 1; ci <= n - 1; ci++)for(int di = ci + 1; di <= n; di++)if( (bi-ai) == 2*(di-ci) ){   // 如果找到一组符合要求的魔法值，则更新各数字在对应位置出现的次数// 考虑到不同的魔法球会有相同的魔法值，所以在作组合计算时对其余位置作数量的乘法cnta[ai] += ge[bi] * ge[ci] * ge[di];cntb[bi] += ge[ai] * ge[ci] * ge[di];cntc[ci] += ge[ai] * ge[bi] * ge[di];cntd[di] += ge[ai] * ge[bi] * ge[ci];break;	// 1个abc只能对应1个d，如果找到了，直接退出循环}for(int i = 1; i <= m; i++){int t = node[i].val;printf("%d %d %d %d\n",cnta[t], cntb[t], cntc[t], cntd[t]);}return 0;
}

以上代码优化后可以拿到80%分数。
继续优化。

解法三、四层循环优化为三层

在这里插入图片描述

公式 ①②③ 告诉了我们几组关系，
1、如果CD之间的距离为一个步长，则AB之间的距离必为两倍步长，且BC之间的距离要大于六倍步长。
2、假设步长为 k，且已知 ai，则
● bi 可直接推断出为 = ai+2k
● ci 的左边界可以推断出 = ai + 8k + 1，从左边界向右枚举即可
● di 可直接推断出为 = ci+k = ai + 9k + 1
如此一来，之前的四层for循环就变成了三层。只需要枚举步长k，ai和ci即可。代码见下

#include <bits/stdc++.h>
#define MAXN 40005
using namespace std;struct Node
{int val, id;	// 存储节点的值和 id。 id用于最终的输出
};
Node node[MAXN];int n, m;	// m 个魔法物； 魔法值不超过 n
int ge[MAXN]; // 记录val为i的魔法物的个数。用于计算组合
int cnta[MAXN], cntb[MAXN], cntc[MAXN], cntd[MAXN];		// cnta[i]表示val为i的魔法物在A位置出现的次数
// cntb[i]表示val为i的魔法物在B位置出现的次数, cntc[i]表示val为i的魔法物在C位置出现的次数 等// 暴力枚举 90% 分数
int main()
{scanf("%d%d",&n, &m);int x;for(int i = 1; i <= m; i++){scanf("%d", &x);node[i].val = x;node[i].id = i;ge[x]++;  // 统计魔法值为x的物品个数}for(int k = 1; 9 * k < n; k++ )for(int ai = 1; ai <= n - 9*k; ai++)	// ai步长为2，可保证bi-ai为2的整数倍{int bi = ai + 2*k;for(int ci = ai + 8*k + 1; ci <= n - k; ci++)	// 根据公式3，枚举ci{				int di = ci + k;cnta[ai] += ge[bi] * ge[ci] * ge[di];cntb[bi] += ge[ai] * ge[ci] * ge[di];cntc[ci] += ge[ai] * ge[bi] * ge[di];cntd[di] += ge[ai] * ge[bi] * ge[ci];				}	}						for(int i = 1; i <= m; i++){int t = node[i].val;printf("%d %d %d %d\n",cnta[t], cntb[t], cntc[t], cntd[t]);}return 0;
}

以上代码优化后可以拿到90%分数。依然没达到满分。
继续优化。

解法四、三层循环优化为两层（前缀和+后缀和）

三层for循环依然会超时，故如果满分需要压缩到2层for循环。我们看下面这张图，会发现：

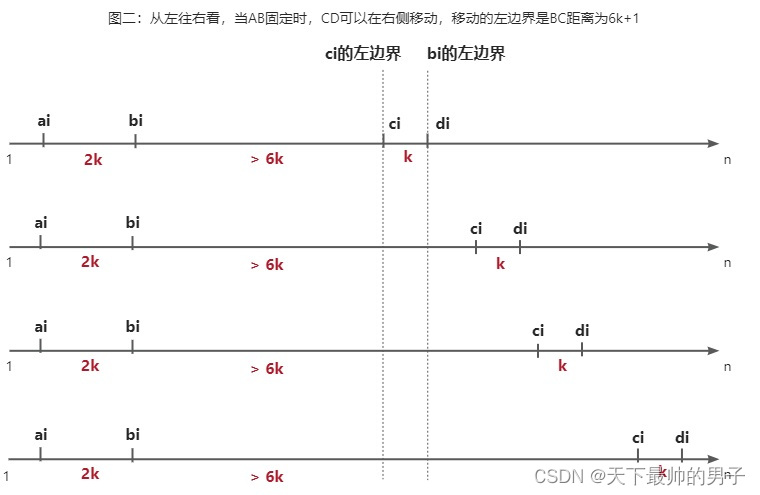
1、从右往左看，当 CD固定 时，AB可以移动，移动的 右边界 是BC距离为6k+1。
即：右边界左侧的 每一对 间隔步长为 2k 的 AB 都符合题意。所以对AB点的计算可以采用 前缀和。

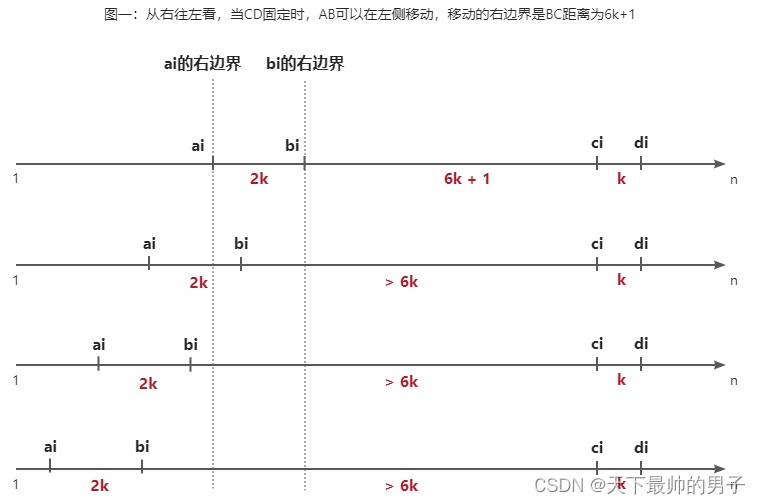
在这里插入图片描述

2、同理（图二），从左往右 看，当 AB固定时，CD可以移动，移动的 左边界 是BC距离为6k+1。
即：左边界右侧 的每一对间隔步长为 k 的 CD 都符合题意。所以对CD点的计算可以采用后缀和（因为从后往前计算）。

在这里插入图片描述

详细代码见下：

#include <bits/stdc++.h>
#define MAXN 40005
using namespace std;struct Node
{int val, id;	// 存储节点的值和 id。 id用于最终的输出
};
Node node[MAXN];int n, m;	// m 个魔法物； 魔法值不超过 n
int ge[MAXN]; // 记录val为i的魔法物的个数。用于计算组合
int cnta[MAXN], cntb[MAXN], cntc[MAXN], cntd[MAXN];		// cnta[i]表示val为i的魔法物在A位置出现的次数
// cntb[i]表示val为i的魔法物在B位置出现的次数, cntc[i]表示val为i的魔法物在C位置出现的次数 等// 暴力枚举 90% 分数。
// 枚举ai，bi，ci。根据公式2，如果bi-ai不满足是2的倍数，则不存在ci和di，故直枚举下一个bi。
// 由于1个ai、bi、ci只能对应1个di。所以在枚举ci时，对di进行直接计算即可。
int main()
{scanf("%d%d",&n, &m);int x;for(int i = 1; i <= m; i++){scanf("%d", &x);node[i].val = x;node[i].id = i;ge[x]++;  // 统计魔法值为x的物品个数}// 3层for循环依然会超时，故需要压缩到2层for循环// 由于当 di 固定时，ci 就固定。当 ci 固定时，bi能移动的右边界就固定，ai的右边界也就固定。所以，只要不超过右边界的每一对bi和ai都满足已知固定di和ci的魔法阵。// 所以，当di和ci固定时，只有bi和ai是变量，此时对每一对bi和ai求前缀和。同理，当ai 和 bi 固定时，对每一对ci和di求后缀和。for(int k = 1; 9 * k < n; k++ ){int sumab = 0;// 因为对ai和bi求前缀和，所以di枚举的顺序是从小到大。所以di从9*k + 2开始（9*k+1+A的起始是1）for(int di = 9*k + 2; di <= n; di++){int ci = di - k;	// 当 di 固定时，ci 也固定int bi = di - 7*k - 1; // 当ci固定时，bi的右边界可固定int ai = di - 9*k - 1; // 当bi的右边界固定时，ai的右边界也可固定sumab += ge[ai] * ge[bi];	// 由于di是从最小值枚举，所以ai和bi可以用前缀和记录每一组有效状态cntc[ci] += sumab * ge[di];cntd[di] += sumab * ge[ci];}int sumcd = 0;for(int ai = n - 9*k - 1; ai >= 1; ai--){int bi = ai + 2*k;  // 当 ai 固定时，bi 也固定int ci = ai + 8*k + 1; // 当bi固定时，ci的左边界可固定int di = ai + 9*k + 1; // 当ci的左边界固定时，di的左边届也固定sumcd += ge[ci] * ge[di];  // 由于ai是从大到小枚举，所以ci和di可以用后缀和cnta[ai] += ge[bi] * sumcd; cntb[bi] += ge[ai] * sumcd;}      }				for(int i = 1; i <= m; i++){int t = node[i].val;printf("%d %d %d %d\n",cnta[t], cntb[t], cntc[t], cntd[t]);}return 0;
}