线上OJ： 一本通：http://ybt.ssoier.cn:8088/problem_show.php?pid=1969 核心思想： 解法1、由于数据量只有 10000 天，估可以采用 模拟每一天 的方式。 #include <bits/stdc++.h>using namespace std;int k = 0;int main(){int ans = 0, coin = 1

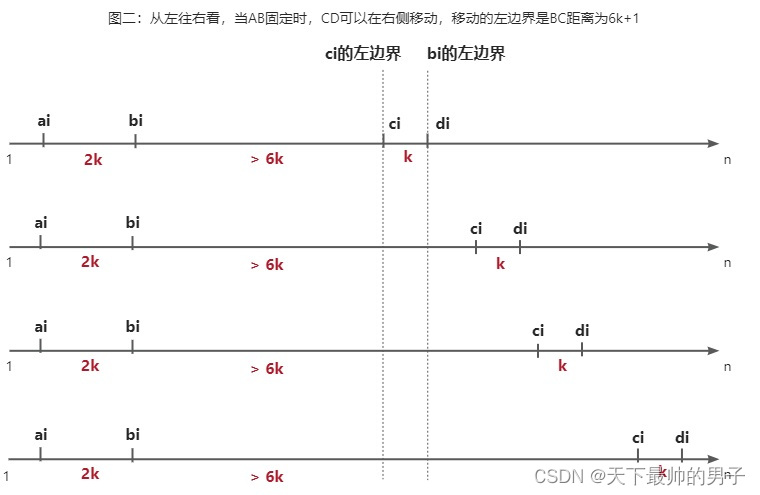
线上OJ： 一本通：http://ybt.ssoier.cn:8088/problem_show.php?pid=1976 本题作为第四题，想拿满分有难度。但是暴力拿些分还是做得到的。 满分需要用 前缀和 来化简for循环。 核心语句： $ x_a < x_b < x_c < x_d $ ① $ x_b - x_a = 2(x_d - x_c) $ ② $ x_b - x_a

线上OJ： 一本通：http://ybt.ssoier.cn:8088/problem_show.php?pid=1973 核心思想： 向上取整的代码 (m+ (n-1))/n 。（本题考点与2023年J组的第一和第二题一样） 比如需要买31支笔，每包30支，则需要买 （31+30-1）/30 = 60/30 = 2包 比如需要买57支笔，每包30支，则需要买 （57+30-1）/

题目描述 组合数 C_n^mCnm​ 表示的是从 nn 个物品中选出 mm 个物品的方案数。举个例子，从 (1,2,3)(1,2,3) 三个物品中选择两个物品可以有 (1,2),(1,3),(2,3)(1,2),(1,3),(2,3) 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 C_n^mCnm​ 的一般公式： C_n^m=\frac{n!}{m!(n-m)!}Cn