本文主要是介绍【树哈希】CF1182D Complete Mirror,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
CF1182D - Complete Mirror
Description
给定一个 n n n 个点的无根树,求一个树根 r o o t root root,使得对于任意两个节点 v 1 , v 2 v_1,v_2 v1,v2,若满足 d i s t ( v 1 , r o o t ) = d i s t ( v 2 , r o o t ) dist(v_1,root)=dist(v_2,root) dist(v1,root)=dist(v2,root),则必有 d g r ( v 1 ) = d g r ( v 2 ) dgr(v_1)=dgr(v_2) dgr(v1)=dgr(v2),无解输出 − 1 -1 −1。
d i s t ( u , v ) dist(u,v) dist(u,v)定义为 u , v u,v u,v 之间的边数, d g r ( v ) dgr(v) dgr(v) 定义为与 v v v 点直接相连的点的个数。
Solution
如果以某一个点为根时,树满足如上条件的充分必要条件为在第一个分叉点的所有儿子所构成的子树均为同构的。
例:
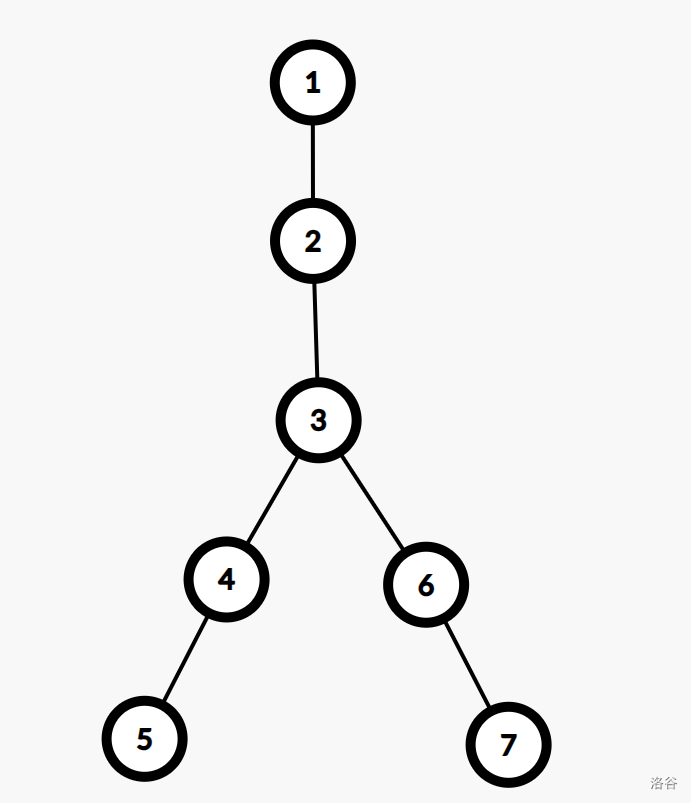
如图,第一个分叉点为 3 3 3 号点,所有儿子为 4 , 5 4,5 4,5 号点,显然他们所构成的子树是同构的。
那么,问题变成了如何找出第一个分叉点以及判断子树均同构。
子树均同构
树哈希是解决这一类问题最有效的办法,当然树哈希也有好几种,这里小编采取 这一种。
不过,由于该题有换根操作,所以需要考虑如何换根:
令 d p ( u ) dp(u) dp(u) 表示以 u u u 为根的子树的哈希值,那么 d p ( u ) = ∑ v ∈ s o n ( u ) ( 1 + f ( d p ( v ) ) ) dp(u)=\sum_{v\in son(u)}(1+f(dp(v))) dp(u)=∑v∈son(u)(1+f(dp(v)))
对于一棵树:
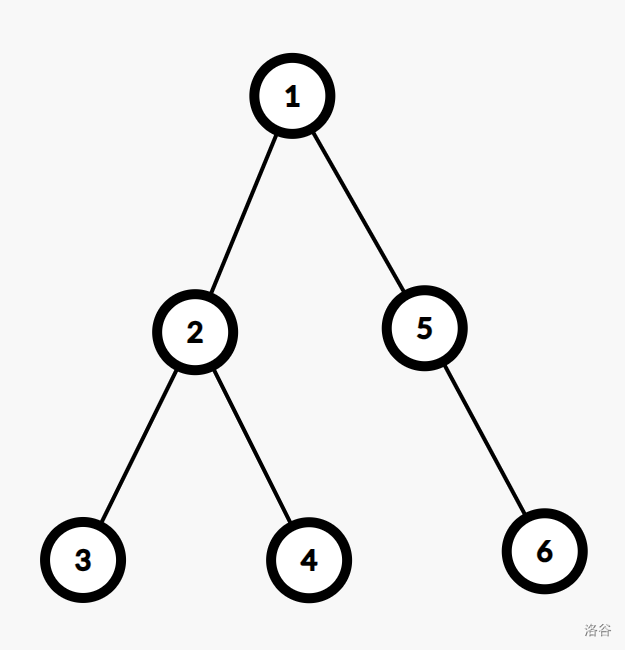
如果从以 1 1 1 为根换到以 2 2 2 为根,那么哪些子树的哈希值会发生变化呢? 1 1 1 号和 2 2 2 号节点的子树的哈希值会发生变化,其余均不发生任何变化。
考虑 1 1 1 号节点子树哈希值:
- 原来: d p ( 1 ) = 1 + f ( d p ( 2 ) ) + 1 + f ( d p ( 5 ) ) dp(1)=1+f(dp(2))+1+f(dp(5)) dp(1)=1+f(dp(2))+1+f(dp(5))
- 现在: d p ( 1 ) = 1 + f ( d p ( 5 ) ) dp(1)=1+f(dp(5)) dp(1)=1+f(dp(5))
故,当 u u u 换根到 v v v 时, d p ( u ) = d p ( u ) − 1 − f ( d p ( v ) ) dp(u)=dp(u)-1-f(dp(v)) dp(u)=dp(u)−1−f(dp(v))。
考虑 2 2 2 号节点子树哈希值:
- 原来: d p ( 2 ) = 1 + f ( d p ( 3 ) ) + 1 + f ( d p ( 4 ) ) dp(2)=1+f(dp(3))+1+f(dp(4)) dp(2)=1+f(dp(3))+1+f(dp(4))
- 现在: d p ( 2 ) = 1 + f ( d p ( 3 ) ) + 1 + f ( d p ( 4 ) ) + 1 + f ( d p ( 1 ) ) dp(2)=1+f(dp(3))+1+f(dp(4))+1+f(dp(1)) dp(2)=1+f(dp(3))+1+f(dp(4))+1+f(dp(1)),注意这里的 d p ( 1 ) dp(1) dp(1) 为更改后的 d p dp dp 值。
故,当 u u u 换根到 v v v 时, d p ( v ) = d p ( v ) + 1 + f ( d p ( v ) ) dp(v)=dp(v)+1+f(dp(v)) dp(v)=dp(v)+1+f(dp(v)),注意这里的 d p ( v ) dp(v) dp(v) 为更改后的 d p dp dp 值。
这样,就可以快速判断子树同构了!
第一个分叉点
这个确实不是很好直接干,直接干容易超时,不过转化一下:当以该分叉点为根时会发生什么?
若树为如下所示:
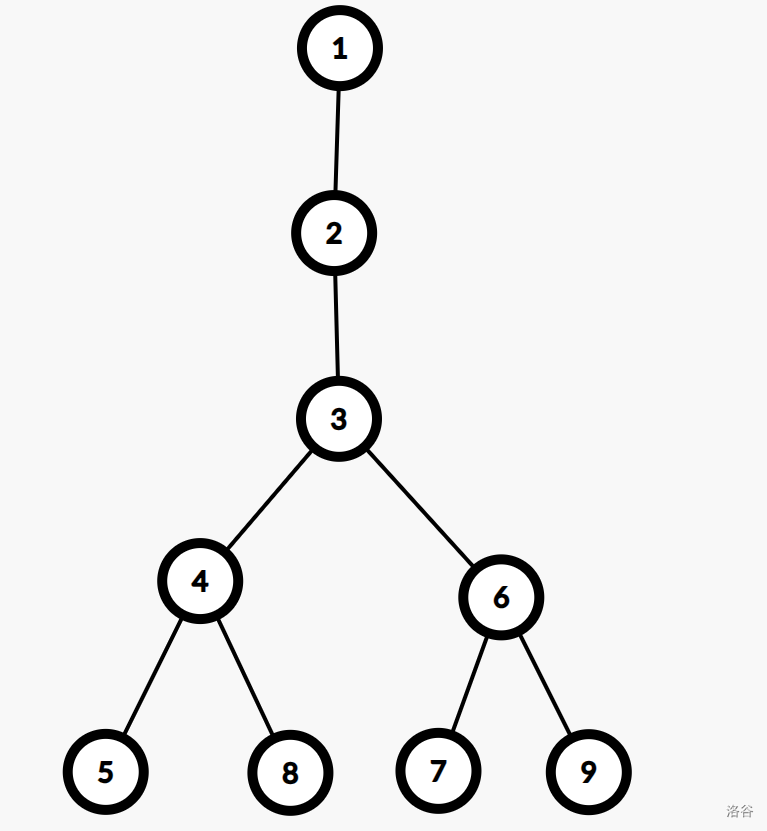
第 1 1 1 个分叉点为 3 3 3,将 3 3 3 为根时:
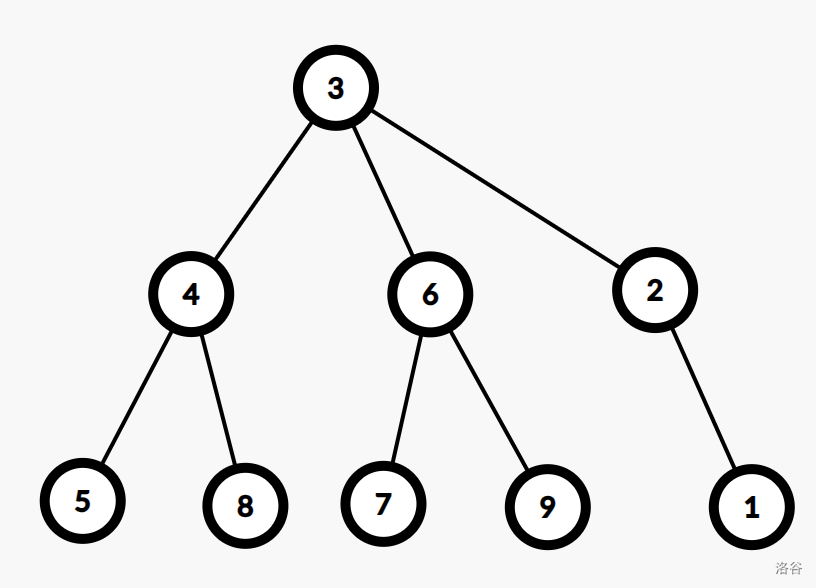
可以发现如果以分界点为根时,有 1 1 1 条链以及其余子树均同构,那么把这条链的端点移为根时,那么就是一颗满足条件的树,故这时候输出那条链的端点即可。
其余情况就判断所有儿子的子树是否均同构即可。更多小细节留给大家思考,这里不再赘述。
Code
其中代码前半段为取模板子,删掉后大概 112 112 112 行。
#include <bits/stdc++.h>
#define fi first
#define se second
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int MOD = 1e9 + 7;
int ksm(int a, int b) {int res = 1;while (b) {if (b & 1) res = res * a % MOD;a = a * a % MOD;b >>= 1;}return res;
}
void exgcd(int a, int b, int &x, int &y) {if (!b) {x = 1, y = 0;return;}exgcd(b, a % b, y, x);y -= a / b * x;
}
struct Mint {int v;void assign(int x) {v = x;}Mint operator+ (const Mint tmp)const {Mint res;res.v = (v + tmp.v) % MOD;return res;}Mint operator+ (const int tmp)const {Mint res;res.v = (v + tmp) % MOD;return res;}Mint operator- (const Mint tmp)const {Mint res;res.v = (v - tmp.v + MOD) % MOD;return res;}Mint operator- (const int tmp)const {Mint res;res.v = (v - tmp + MOD) % MOD;return res;}Mint operator* (const Mint tmp)const {Mint res;res.v = v * tmp.v % MOD;return res;}Mint operator* (const int tmp)const {Mint res;res.v = v * tmp % MOD;return res;}Mint operator/ (const Mint tmp)const {int x, y;exgcd(tmp.v, MOD, x, y), x = (x % MOD + MOD) % MOD;Mint res;res.v = v * x % MOD;return res;}Mint operator/ (const int tmp)const {int x, y;exgcd(tmp, MOD, x, y), x = (x % MOD + MOD) % MOD;Mint res;res.v = v * x % MOD;return res;}Mint operator^ (Mint b)const {Mint ans;ans.v = ksm(v, b.v);return ans;}Mint operator^ (int b)const {Mint ans;ans.v = ksm(v, b);return ans;}void read() {string s;cin >> s;for (auto i : s)v = (v * 10 + i - '0') % MOD;}
};const int N = 1e5 + 10;int n;
std::vector<int> G[N];
Mint dp[N];
int far[N];Mint h(Mint x) {return x * x * x * 1237123 + 1145141;
}
Mint f(Mint x) {Mint ok, res;res.v = 0;ok.v = (x.v & ((1ll << 31) - 1)), res = res + h(ok);ok.v = (x.v >> 31), res = res + h(ok);return res;
}
Mint dfs1(int u, int fa) {for (auto v : G[u]) {if (v == fa) continue;dp[u] = dp[u] + 1 + f(dfs1(v, u));}return dp[u];
}
void dfs2(int u, int fa) {unordered_map<int, int> cnt;int tot = 0;for (auto v : G[u]) {cnt[dp[v].v] ++, tot ++;}if (tot >= 3) {if (cnt.size() == 2) {for (auto v : G[u])if (cnt[dp[v].v] == 1 && far[v]) {cout << far[v] << endl;exit(0);}}if (cnt.size() == 1) {cout << u << endl;exit(0);}} else if (tot == 2) {if (cnt.size() == 1) {cout << u << endl;exit(0);}}for (auto v : G[u]) {if (v == fa) continue;Mint tmp1 = dp[u], tmp2 = dp[v];int tf1 = far[v], tf2 = far[u];dp[u] = dp[u] - 1 - f(dp[v]), dp[v] = dp[v] + 1 + f(dp[u]);if (G[u].size() == 2) {if (v == G[u][0] && far[G[u][1]]) far[u] = far[G[u][1]];if (v == G[u][1] && far[G[u][0]]) far[u] = far[G[u][0]];} else if (G[u].size() == 1) {far[u] = u;}far[v] = 0;dfs2(v, u);dp[u] = tmp1, dp[v] = tmp2, far[v] = tf1, far[u] = tf2;}
}
void dfs3(int u, int fa) {int tot = 0, p;for (auto v : G[u]) {if (v == fa) continue;tot ++, p = v;dfs3(v, u);}if (tot == 1) far[u] = far[p];if (tot == 0) far[u] = u;
}signed main() {cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> n;int u, v, fir = 0;for (int i = 1; i < n; i ++) {cin >> u >> v, G[u].emplace_back(v), G[v].emplace_back(u);if (!fir) fir = u;}dfs1(1, -1);dfs3(1, -1);if (far[1] || (G[1].size() == 2 && far[G[1][0]] && far[G[1][1]])) {if (far[1]) cout << 1 << endl;else cout << far[G[1][0]] << endl;return 0;}dfs2(1, -1);cout << -1 << endl;return 0;
}
这篇关于【树哈希】CF1182D Complete Mirror的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!