本文主要是介绍Isolation Forest 简介,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 简介
孤立森林 iForest(Isolation Forest)是一种无监督学习算法,用于识别异常值。其基本原理是:异常数据由于数量较少且与正常数据差异较大,因此在被隔离时需要较少的步骤。
两个假设:
1. 异常的值是非常少的(如果异常值很多,可能被识别为正常的);
2. 异常值与其他值的差异较大(主要是全局上都为异常的异常,局部小异常可能发现不了,因为差异并不大)。
2. 具体流程
2.1 训练森林
子采样: 首先从整个数据集中随机抽取一定数量的样本来为构建树做准备。这些抽样的子集大小通常远小于原始数据集的大小,这样可以限制树的大小,并且减少计算复杂度。
构建孤立树 (iTrees): 对于每个子采样集,算法构建一棵孤立树。构建孤立树的过程是递归的。在每个节点,算法随机选择一个特征,并在该特征的最大值和最小值之间随机选择一个分割值。然后,数据根据这个分割值将样本分到左子树或右子树(这里其实就是简单的将样本中特征小于这个分割点的样本分到左边,其次分到右边)。这个过程的结束条件:树达到限定的高度, 节点中的样本数量到一定的数目,或者所有样本的所选特征值都是同一个值。
森林构建: 重复1-2构建完特定数量的孤立树,集合为孤立森林。
2.2 首先要明确几个相关概念
路径长度( h ( x ) h(x) h(x)): 指样本通过该孤立树构建阶段的特征选择方式,从树的根节点到达该样本被孤立的节点(被孤立就是意味着这个样本最终到达的树的叶子节点)所需要的边数。
平均路径长度 E ( h ( x ) ) E(h(x)) E(h(x)): 该样本在森林中所有树的路径长度的平均值。
树的平均路径长度:
c ( n ) = 2 H ( n − 1 ) − 2 ( n − 1 ) n c(n)=2H(n-1)-\frac{2(n-1)}{n} c(n)=2H(n−1)−n2(n−1)
-----
iForest 适用于连续数据的异常检测,将异常定义为 容易被孤立的离群点。 具体的,确定一个维度的特征,
并在最大值和最小值之间随机选择一个值 x ,然后按照小于 x 和 大于等于x 可以把数据分成左右两组。
然后再随机的按某个特征维度的取值把数据进行细分,重复上述步骤,直到无法细分,
直到数据不可再分。直观上,异常数据较少次切分就可以将它们单独划分出来,而正常数据恰恰相反。
sklearn.ensemble.IsolationForest
contamination:默认为auto,数据集中异常样本的比例
优点:高精准度
3. 算法优缺点
3.1 优点
1. 高效性:IF特别适合处理大数据集。它具有线性的时间复杂度,并且由于使用了子采样,使得在计算上更加高效。
2. 易于并行化: 和RF一样,构建孤立树是独立的过程,构建森林可以并行化。
3.2 缺点
1. 异常值比例敏感性: 如果数据集中异常值的比例相对较高,其效果可能就会下降,因为它是基于异常值“少而不同”的假设。
2. 对局部异常检测不敏感:因为 “少而不同的” 前提条件决定主要解决全局异常的特点,对在局部区域表现出轻微异常特征的点检测不是很敏感。
3. 不适用于特别高维的数据:IF不会因为特征的多少而降低算法的效率,但也正因为每次只随机用其中一个特征作为分割的特征,如果特征维度很高,就会有很多特征没有用到。
4. demo
4.1 数据准备
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_splitn_samples, n_outliers = 120, 10
rng = np.random.RandomState(0)
cluster_1 = 0.4 * rng.randn(n_samples, 2) + np.array([2, 2])
cluster_2 = 0.3 * rng.randn(n_samples, 2) + np.array([-2, -2])
outliers = rng.uniform(low=-4, high=4, size=(n_outliers, 2))
X = np.concatenate([cluster_1, cluster_2, outliers])
y = np.concatenate([np.ones((2 * n_samples), dtype=int), -np.ones(n_outliers, dtype=int)])scatter = plt.scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor="k")
handles, labels = scatter.legend_elements()
plt.axis("square")
plt.legend(handles=handles, labels=["outliers", "inliers"], title="true class")
plt.title("data distribution")
plt.show()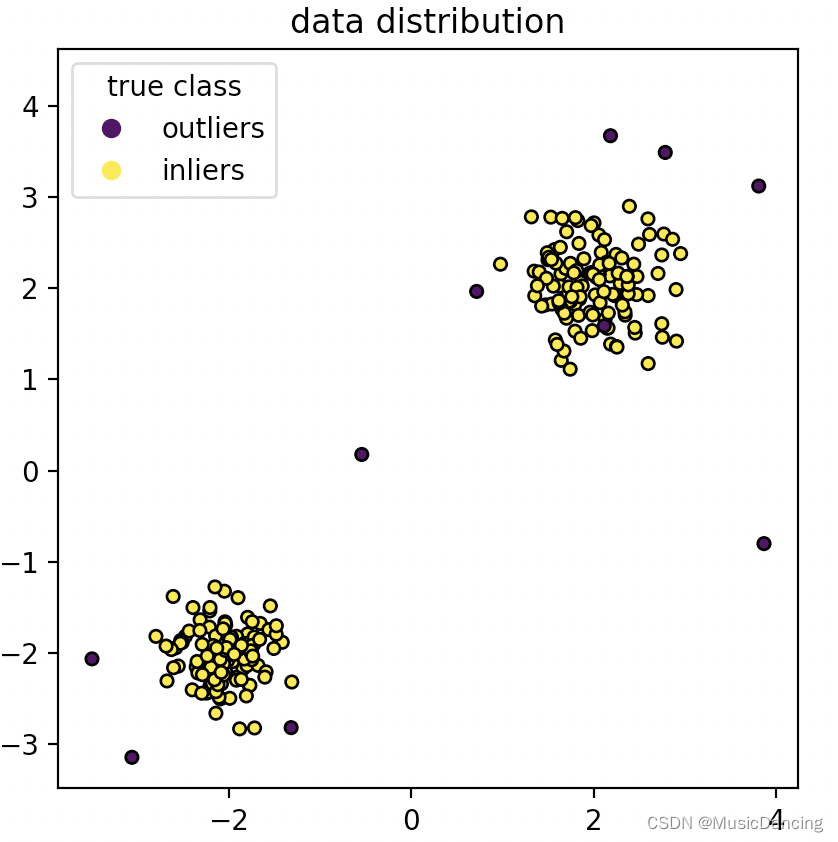
4.2 模型预测&可视化
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_splitn_samples, n_outliers = 120, 10
rng = np.random.RandomState(0)
cluster_1 = 0.4 * rng.randn(n_samples, 2) + np.array([2, 2])
cluster_2 = 0.3 * rng.randn(n_samples, 2) + np.array([-2, -2])
outliers = rng.uniform(low=-4, high=4, size=(n_outliers, 2))
X = np.concatenate([cluster_1, cluster_2, outliers])
y = np.concatenate([np.ones((2 * n_samples), dtype=int), -np.ones(n_outliers, dtype=int)])X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
from sklearn.ensemble import IsolationForest
clf = IsolationForest(max_samples=100, random_state=0)
clf.fit(X_train)
y_pre_score_test = clf.decision_function(cluster_1) # -1为异常, 1为正常,
y_pre_label_test = clf.predict(cluster_1)# ---------结果可视化--------------
# 通过网格的方式得到location的x和y坐标
xx, yy = np.meshgrid(np.linspace(-6, 6, 60), np.linspace(-6, 6, 60))
# concat x和y 得到输入的坐标
input_location = np.c_[xx.ravel(), yy.ravel()]
Z = clf.decision_function(input_location)
Z = Z.reshape(xx.shape)plt.title("IsolationForest")
plt.contourf(xx, yy, Z, camp=plt.cm.Blues_r)
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=20, edgecolor='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green', s=20, edgecolor='k')
c = plt.scatter(outliers[:, 0], outliers[:, 1], c='red', s=20, edgecolor='k')
plt.axis('tight')
plt.xlim((-6, 6))
plt.ylim((-6, 6))
plt.legend([b1, b2, c], ["train data", "test data", "outlier"], loc="best")
plt.show()
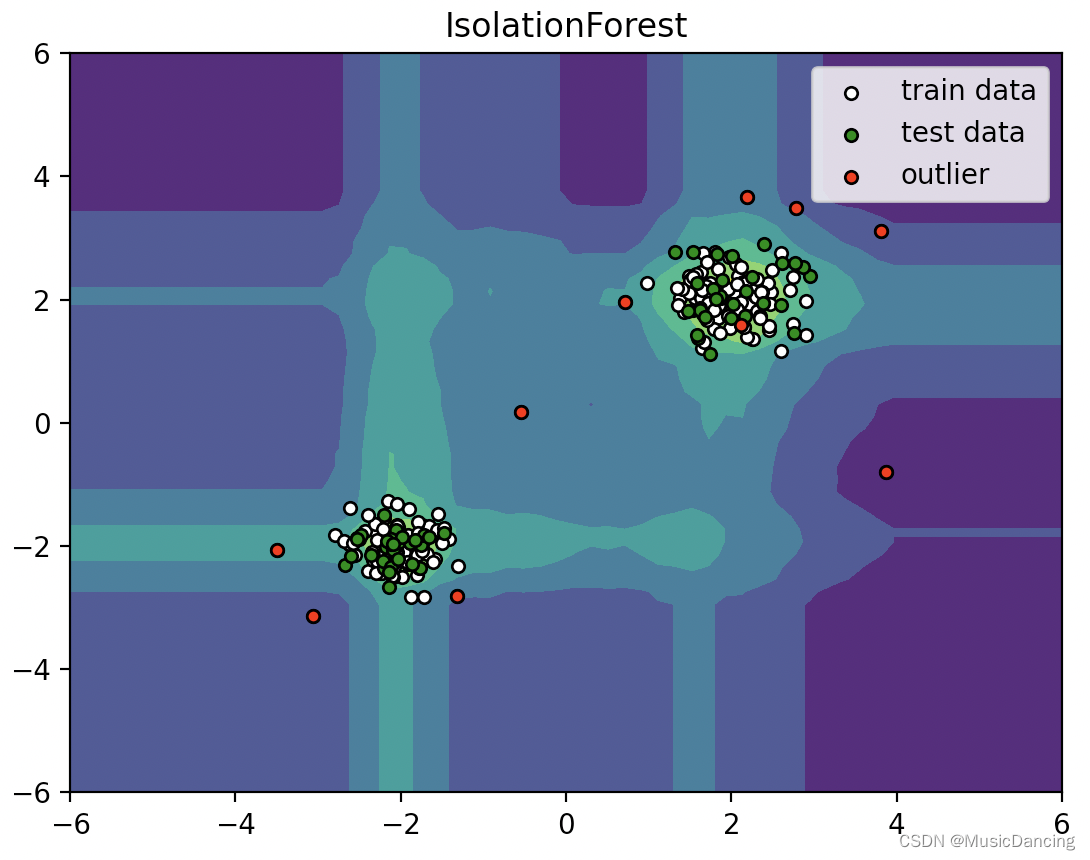
这篇关于Isolation Forest 简介的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



