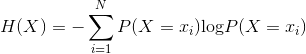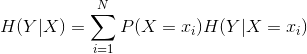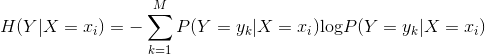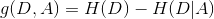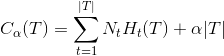信息增益与决策树

本文主要是介绍信息增益与决策树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

决策树是一种判别式模型。在一颗分类决策树中，非叶子节点时决策规则，叶子节点是类别。当输入一个特征向量时，按照决策树上的规则从根节点向叶节点移动，最后根据叶节点的类别判定输入向量的类别。决策树也可以用来解决回归问题。

建立一个决策树模型主要有三个步骤：特征选择、决策树的生成、决策树的剪枝。而特征选择时要用到信息增益这个概念。

特征选择：

对于一个随机变量X，它的熵可以表示为：

对于两个随机变量X、Y，在已知X的情况下，Y的条件熵为：

其中，

而信息增益（IG）或互信息（MI）的定义是：

也就是说在已知A的情况下随机变量D的不确定性的减少程度，也就是在我们知道A的情况下获得了多少信息。

如果D是数据类别的随机变量，而A是数据某个特征的随机变量，可以想见使得信息增益最大的特征是最好的特征。因为这个特征可以最大程度上减少我们对类别的不确定性。

所以在决策树模型中，使用信息增益来进行每一层的特征选择。

决策树的生成：

在特征选择的方案确定之后，建立决策树的过程就很简单了：首先根节点是所有类别；选择使得信息增益最大的特征对根节点进行划分，生成若干个子节点；递归的进行上述过程。

在建立决策树的过程中要设置终止条件，一个显而易见的终止条件是某个节点内的数据属于同一类，其他的如信息增益小于某个阈值等。当叶节点内的数据类别不一致时，使用该节点内类别的众数作为该叶节点的类别，这也是经验风险最小的结果。

决策树的剪枝：

如果决策树的层次很深、叶子节点很多的话，那么会对训练数据有很好的分类结果。试想一种极端的情况是每个叶节点只有一个训练数据，那么该模型对训练数据的分类误差是0。决策树的层次越高，或者决策树的叶节点越多，模型也就越复杂，越容易产生过拟合。跟其他的机器学习方法一样，这时需要进行正则化，也就是对决策树的模型复杂度进行惩罚。

设决策树T的叶节点个数是|T|，t是T的叶节点，该节点有Nt个样本，其中属于第k类的有Ntk个。Ht(T)为节点t上的经验熵（提到经验就是只跟训练数据有关），其计算方法跟上面熵的定义相同。
则决策树的学习损失函数定义为：

在公式的右半部，第一项表示模型对训练数据的误差，第二项是模型的复杂度，a是两者之间的平衡因子。根据该损失函数就可以训练出结构风险最小的决策树了。

上面是最简单的决策树的建模过程，下面简单提一下随机森林的概念：节选自http://www.cnblogs.com/wentingtu/archive/2011/12/22/2297405.html

随机森林：

随机森林顾名思义，是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。

在建立每一棵决策树的过程中，有两点需要注意 - 采样与完全分裂。首先是两个随机采样的过程，random forest对输入的数据要进行行、列的采样。对于行采样，采用有放回的方式，也就是在采样得到的样本集合中，可能有重复的样本。假设输入样本为N个，那么采样的样本也为N个。这样使得在训练的时候，每一棵树的输入样本都不是全部的样本，使得相对不容易出现over-fitting。然后进行列采样，从M 个feature中，选择m个(m << M)。之后就是对采样之后的数据使用完全分裂的方式建立出决策树，这样决策树的某一个叶子节点要么是无法继续分裂的，要么里面的所有样本的都是指向的同一个分类。一般很多的决策树算法都一个重要的步骤 - 剪枝，但是这里不这样干，由于之前的两个随机采样的过程保证了随机性，所以就算不剪枝，也不会出现over-fitting。

按这种算法得到的随机森林中的每一棵都是很弱的，但是大家组合起来就很厉害了。我觉得可以这样比喻随机森林算法：每一棵决策树就是一个精通于某一个窄领域的专家（因为我们从M个feature中选择m让每一棵决策树进行学习），这样在随机森林中就有了很多个精通不同领域的专家，对一个新的问题（新的输入数据），可以用不同的角度去看待它，最终由各个专家，投票得到结果。

随机森林是一个最近比较火的算法，它有很多的优点：

1. 在数据集上表现良好；
2. 在当前的很多数据集上，相对其他算法有着很大的优势；
3. 它能够处理很高维度（feature很多）的数据，并且不用做特征选择；
4. 在训练完后，它能够给出哪些feature比较重要；
5. 在创建随机森林的时候，对generlization error使用的是无偏估计；
6. 训练速度快；
7. 在训练过程中，能够检测到feature间的互相影响；
8. 容易做成并行化方法；
9. 实现比较简单。

这篇关于信息增益与决策树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！