本文主要是介绍蓝桥杯第十三届c++大学B组详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.九进制转十进制
2.顺子日期
3.刷题统计
4.修剪灌木
5.x进制的减法
6.统计子矩阵
7.积木画
8.扫雷
9.李白打酒
10.砍竹子
1.九进制转换十进制

题目解析:就是将2022的每一位拿出来乘以9的n-1次方的和就是最终答案。次方是从0开始的到n-1.
#include <iostream>
using namespace std;int pow(int a, int b)
{int ret = 1;if(b == 0)return 1;else{while(b--){ret *= a;}}return ret;
}int main()
{int n = 2022;int change = 0;for(int i = 0; i <= 3; i++){int t = n % 10;change += pow(9, i) * t;n /= 10;}cout << change << endl;return 0;
}2.顺子日期

题目解析:这个题目手算也很快.
012 123 234 345...
因为月日的要求只能有012 和123;
那么就只要将数字全部转变为字符串,然后再找上面两个字符存不存在就可以确定了。
#include <iostream>
#include<string>
using namespace std;bool check(int year, int month, int day)
{string str = to_string(year);if(month < 10) str += '0';str += to_string(month);if(day < 10)str += '0';str += to_string(day);return (str.find("012") != -1 || str.find("123") != -1);
}int main()
{int year = 2022;int ans = 0;int Month[13] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};for(int month = 1; month <= 12; month++){for(int day = 1; day <= Month[month]; day++){if(check(year, month, day)){ans++;}}}cout << ans << endl;return 0;
}3.刷题统计

题目解析:题目比较简单,就是加和加上判断。最后返回日期即可。
#include <iostream>
using namespace std;int main()
{long long a, b, n;cin >> a >> b >> n;long long sum = 0;long long day = 0;while(1){ if(sum >= n){cout << day << endl;return 0;}for(int i = 1; i <= 7; i++){if(sum >= n){cout << day << endl;return 0;}if(i >= 1 && i <= 5){sum += a;}else{sum += b;}day++;}}return 0;
}后面想了一下只过了6个用例,那么就是数据肯定太大,处理出错了.
#include <iostream>
using namespace std;int main()
{long long a, b, n;cin >> a >> b >> n;long long week = a * 5 + b * 2;//一周做题量long long num = (n / week) * week;//花费周数的做题量;long long day = (n / week) * 7;//花费天数.while(n - num > 0){if(day % 7 < 5)num += a;elsenum += b;day++;}cout << day << endl;return 0;
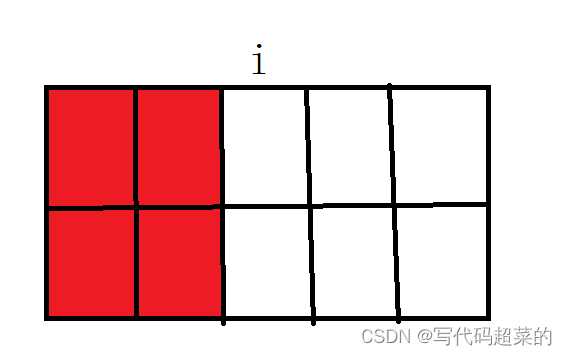
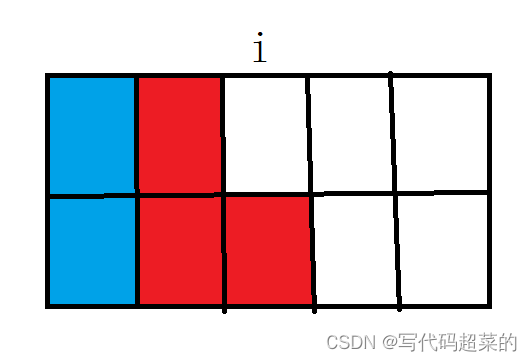
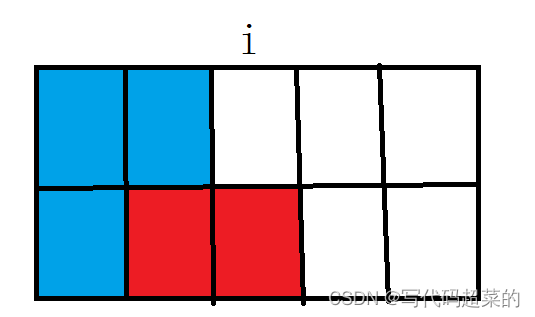
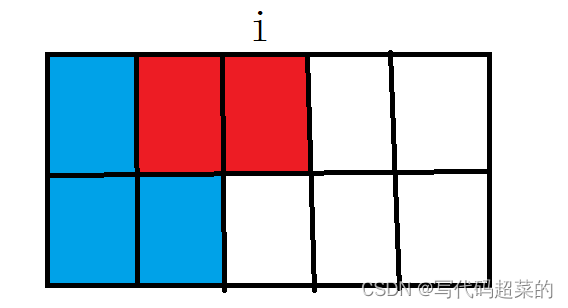
}4.修剪灌木

题目解析:这个题目;自己可以写几个看看规律。
每次剪树的移动时间就会给树的生长提供时间间隙;
那么就可以分三种情况:
1.从左到右边进行剪第一次,那么就是从开始剪的地方到现在剪的地方的天数就是可以长高的高度就是i。
2.从左到右边再从右边拐到左边剪,那么就是 i, i + 1, i + 2, ..., n, n -1 , n - 2, ...., i;
那么生长高度就是2*(n - i);
3.从右边到左边再拐到右边剪,那么就是 i - 1, i -2, i -3 ..., 1, 2, ..., i;
那么生长的高度就是2(i - 1);
#include <iostream>
using namespace std;int maxtreelenth(int a, int b, int c)
{if(a > b){if(a > c)return a;elsereturn c;}else{if(c > b)return c;elsereturn b;}
}int main()
{int n, i;cin >> n;for(int i = 1; i <= n; i++){cout << maxtreelenth(i, 2 * (n - i), 2 * (i - 1)) << endl;}return 0;
}5.x进制的减法

题目解析:可以参考一下这篇博客,暂时我还没想到这个题目如何写.
X 进制减法 — 蓝桥杯E题_x进制减法 100 【题目描述】 进制规定了数字在数位上逢几进一。 x 进制是一种-CSDN博客
#include<iostream>
#include<algorithm>using namespace std;const int N = 1e5 + 10,MOD = 1e9 + 7;int n,m1,m2,m;
int a[N],b[N];int main(){cin >> n >> m1;for(int i = m1 - 1;i >= 0;i --) cin >> a[i];cin >> m2;for(int i = m2 - 1;i >= 0;i --) cin >> b[i];int m = max(m1,m2);int res = 0;for(int i = m;i >= 0;i --){res = (res * (long long)(max({2,a[i] + 1,b[i] + 1})) + a[i] - b[i]) % MOD;}cout << res << endl;return 0;
}
6.统计子矩阵

题目解析:
6.统计子矩阵:

题目解析:前缀和+双指针,将原矩阵加和得到sum矩阵,然后使用双指针进行矩阵的值判断.
例子:
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
sum矩阵:
1 2 3 4
6 8 10 12
15 18 21 24
使用双指针 L 和R 进行遍历矩阵范围的控制.最好自己画一下图更好理解上手,然后去写代码
#include<iostream>
using namespace std;#define maxn 505
int a[maxn][maxn];
int sum[maxn][maxn];int main()
{int n, m, k;cin >> n >> m >> k;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cin >> a[i][j];sum[i][j] = a[i][j] + sum[i - 1][j];}}long long m_cout = 0;for(int x = 1; x <= n; x++){for(int y = x; y <= n; y++){for(int r = 1, l = 1, s = 0; r <= m; r++){s += sum[y][r] - sum[x - 1][r];while(s > k && l < r){s = s - sum[y][l] + sum[x - 1][l];l++;}if(s <= k){m_cout += r - l + 1;}}}}cout << m_cout << endl;return 0;
}7.积木画

题目解析:动态dp解决,要画图更好理解.
dp[i][4]:
dp[i][0]: 表示积木第i列的上下都没有堆积木;
dp[i][1]: 表示积木第i列的上面没有堆积木,下面摆放了积木;
dp[i][2]: 表示积木第i列的下面没有堆积木,上面摆了积木;
dp[i][3]:表示积木第i列的上下都摆放了堆积木;
那我们来看状态方程如何推导:
首先初始化:
当n == 0;dp[0][3] = 1可以理解为全部摆放好了;
当n == 1; dp[1][3] = 1;只有一种摆放方式;
dp[i][0]推导:
那么前面的i -1 一定是以及摆放好的了;所以
dp[i][0] = dp[i - 1][3];
然后就是dp[i][1]:
有下面两种情况:
dp[i][1] = dp[i - 1][0] + dp[i -1][2];
dp[i][2]:
dp[i][2] = dp[i - 1][0] + dp[i - 1][ 1];
dp[i][3]:
dp[i][3] = dp[i - 2][3] + dp[i -1][3] + dp[i - 1][2] +dp[i - 1][1];
#include<iostream>
using namespace std;
#define N 10000001
#define MOD 1000000007int n;
long long dp[N][3];void slove()
{cin >> n;dp[0][3] = 1;dp[1][3] = 1;for(int i = 2; i <= n; i++){dp[i][0] = dp[i - 1][3];dp[i][1] = (dp[i - 1][0] + dp[i -1][2]) % MOD;dp[i][2] = (dp[i - 1][0] + dp[i - 1][ 1]) % MOD;dp[i][3] = ((dp[i - 2][3] + dp[i -1][3]) % MOD + (dp[i - 1][2] +dp[i - 1][1]) % MOD) % MOD;}cout << dp[n][3] << endl;
}int main()
{slove();return 0;
}8.扫雷

题目解析:这个题目一看就是要使用到dfs深搜
#include <iostream>
using namespace std;int n, m;
int a[102][102] = {0};
int dx[8] = {0, 0, -1, 1, -1, -1, 1, 1};
int dy[8] = {-1, 1, 0, 0, -1, 1, -1, 1};
int vis[102][102] = {0};void dfs(int x, int y)
{if(x > n && y > m)return;vis[x][y] = 1;for(int k = 0; k < 8; k++){int xx = dx[k] + x;int yy = dy[k] + y;if(xx >= 1 && x <= n && yy >= 1 && yy <= m){if(a[xx][yy] = 1 && vis[xx][yy] == 0){a[x][y] += a[xx][yy];vis[xx][yy] = 1;dfs(x + 1, y + 1);}}}
}int main()
{cin >> n >> m;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cin >> a[i][j];}}dfs(1, 1);for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cout << a[i][j];}cout << endl;}return 0;
}9.李白打酒

题目解析:又是动态dp,dp[i][j][k]表示遇到第i个店第j个花酒剩下k斗酒的方案数;
初始化: dp[0][0][2] = 1;
当最后一次遇到的是店,动态方程就是 dp[i][j][k] = dp[i][j][k] + dp[i-1][j][k / 2];
因为喝酒的数目和遇到花的次数挂钩,那么最少酒的斗数就是遇到花的次数.
最后一次遇到的是花,那么酒的数量一定要大于大于1;
那么就是dp[i][j][k] = dp[i][j - 1][k + 1];
需要注意最后返回的是dp[n][m - 1][1];因为最后一次遇到花之前必须是至少还剩下一斗酒.
#include <iostream>
using namespace std;
#define N 101long long dp[N][N][N];int main()
{int n, m;cin >> n >> m;dp[0][0][2] = 1;for(int i = 0; i <= n; i++){for(int j = 0; j <= m; j++){for(int k = 0; k <= m; k++){if(i && k % 2 == 0)//遇到店;dp[i][j][k] = dp[i][j][k] + dp[i - 1][j][k / 2];if(j)//遇到花dp[i][j][k] = dp[i][j][k] + dp[i][j - 1][k + 1];}}}cout << dp[n][m - 1][1] << endl;return 0;
}10.砍竹子

题目解析:这个题目用到贪心,暴力;将竹子用魔法公式进行处理,但是如果竹子的长度一样就可以一起砍.得到的次数是一样的.
#include <iostream>
using namespace std;
#include<vector>
#define N 200000
#include<cmath>int n;
vector<long long> e[N]; int main()
{cin >> n;vector<long long> a(n);for(auto& x : a)cin >> x;long long ans = 0;for(int i = 0; i < n; i++){long long tmp = a[i];while(tmp > 1){e[i].push_back(tmp);tmp = sqrt(tmp / 2 + 1);ans++;}}for(int i = 1; i < n; i++){for(long long x : e[i - 1]){for(long long tmp : e[i]){if(x == tmp)ans--;}}}cout << ans << endl;return 0;
}这篇关于蓝桥杯第十三届c++大学B组详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!