本文主要是介绍【鸿蒙千帆起】《开心消消乐》完成鸿蒙原生应用开发,创新多端联动用户体验,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《开心消消乐》已经完成鸿蒙原生应用开发,乐元素成为率先完成鸿蒙原生应用开发的20+游戏厂商之一。作为一款经典游戏,《开心消消乐》已经拥有8亿玩家,加入鸿蒙原生应用生态,将为其带来更优的游戏性能和更多创新体验。自9月25日华为宣布全新HarmonyOS NEXT 蓄势待发、鸿蒙原生应用全面启动以来,以游戏为代表的18个行业,成为加入鸿蒙生态的先行军,呈现出“鸿蒙千帆起”的景象。

早在2014年《开心消消乐》上线之初就接入了华为游戏中心,如今,双方合作已经走过近十个年头。依托长久以来的坚实合作基础、华为游戏中心面向开发者的全周期服务能力,以及华为领先的技术和鸿蒙生态,《开心消消乐》坚定了开发鸿蒙原生应用的信心,走在了鸿蒙生态游戏先锋合作的前列。基于HarmonyOS特性,《开心消消乐》可以更好实现游戏体验的优化,比如,通过HarmonyOS元服务的应用,可以加强游戏与玩家之间交互的提醒,用户不需要频繁打开游戏就能接收到游戏中的关键信息,比如精力恢复、新关卡开放、活动信息提醒等,给玩家提供了更加便捷的游戏体验。
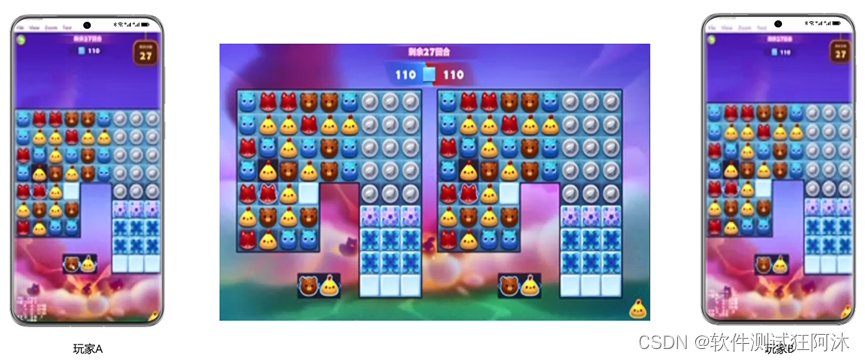
同时,HarmonyOS特有的分布式软总线技术还为用户打造出创新的分布式游戏玩法。通过与HarmonyOS分布式有机结合,可实现多设备协同的分布式PK场景。在此场景下,用户操作各自的HarmonyOS设备,使用智慧屏实时显示对战场景,双方就可以通过大屏及时观察对手棋盘的状况,消除自己棋盘的同时,给对方的棋盘消除制造一些障碍,大大提升了游戏的互动性与趣味性!
最新鸿蒙学习资源整合
在当今的全场景时代下, HarmonyOS不仅仅可以帮助伙伴打造更优质的用户体验,基于强大的AI能力还可以实现精准识别、精确投放,为伙伴提供新流量,并共享全场景服务分发,助力生态共赢。数据显示,截至今年8月份,鸿蒙生态的设备数已超过7亿,鸿蒙生态开发者已超过220万。
这篇关于【鸿蒙千帆起】《开心消消乐》完成鸿蒙原生应用开发,创新多端联动用户体验的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







