小小算式(1 + 2) * (3 + 4)背后的大道理

本文主要是介绍小小算式(1 + 2) * (3 + 4)背后的大道理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

前缀表示法（波兰表达式）

中缀表达法

后缀表达法（逆波兰表达式）

三种表达法的相互转换

练习：逆波兰表达式求值

---

前缀表示法（波兰表达式）

波兰表示法（英语：Polish notation，或波兰记法）是一种逻辑、算术和代数表示方法，其特点是操作符置于操作数的前面，因此也称做前缀表示法。如果操作符的元数是固定的，则语法上不需要括号仍然能被无歧义地解析。波兰记法是波兰数学家扬·武卡谢维奇于1920年代引入的，用于简化命题逻辑。

表达“三加四”时，前缀记法写作“+ 3 4 ”，而不是“3 + 4”。在复杂的表达式中，操作符仍然在操作数的前面，但操作数可能是包含操作符的平凡表达式。 例如，中缀运算式(5 - 6) * 7 ，在前缀表达式中可以表示为：

*(− 5 6) 7

或省略括号：

* - 5 6 7

由于简单的算术运算符都是二元的，该前缀表达式无需括号，且表述是无歧义的。在前面的例子里，中缀形式的括号是必需的，如果将括号移动到：

5 - (6 * 7)

即：

5 - 6 * 7

则会改变整个表达式的值。而其正确的前缀形式是：

- 5 * 6 7

减法运算要等它的两个操作数（5；6和7的乘积）都完成时才会处理。在任何表示法中，最里面的表达式最先运算，而在波兰表达式中，决定“最里面”的是顺序而不是括号。

中缀表达法

中缀表示法（或中缀记法）是一个通用的算术或逻辑公式表示方法， 操作符是以中缀形式处于操作数的中间（例：3 + 4）。与前缀表达式（例：+ 3 4 ）或后缀表达式（例：3 4 + ）相比，中缀表达式不容易被电脑解析逻辑优先顺序，但仍被许多程序语言使用，因为它符合大多数自然语言的写法。

与前缀或后缀记法不同的是，中缀记法中括号是必需的。计算过程中必须用括号将操作符和对应的操作数括起来，用于指示运算的次序。

后缀表达法（逆波兰表达式）

逆波兰表示法（英语：Reverse Polish notation，缩写RPN，或逆波兰记法、逆卢卡西维茨记法），是一种由波兰数学家扬·卢卡西维茨于1920年引入的数学表达式形式，在逆波兰记法中，所有操作符置于操作数的后面，因此也被称为后缀表示法、后序表示法[1]。逆波兰记法不需要括号来标识操作符的优先级。

逆波兰结构由弗里德里希·L·鲍尔和艾兹格·迪科斯彻在1960年代早期提议用于表达式求值，以利用堆栈结构减少计算机内存访问。逆波兰记法和相应的算法由澳大利亚哲学家、计算机学家查尔斯·伦纳德·汉布尔在1960年代中期扩充[2][3]。

在1960和1970年代，逆波兰记法广泛地被用于台式计算器，因此也在普通公众（如工程、商业和金融等领域）中使用。

下面大部分是关于二元运算，一个一元运算使用逆波兰记法的例子是阶乘的记法。

逆波兰记法中，操作符置于操作数的后面。例如表达“三加四”时，写作“3 4 + ”，而不是“3 + 4”。如果有多个操作符，操作符置于第二个操作数的后面，所以常规中缀记法的“3 - 4 + 5”在逆波兰记法中写作“3 4 - 5 + ”：先3减去4，再加上5。使用逆波兰记法的一个好处是不需要使用括号。例如中缀记法中“3 - 4 * 5”与“（3 - 4）*5”不相同，但后缀记法中前者写做“3 4 5 * - ”，无歧义地表示“3 (4 5 *) -”；后者写做“3 4 - 5 * ”。

逆波兰表达式的解释器一般是基于堆栈的。解释过程一般是：操作数入栈；遇到操作符时，操作数出栈，求值，将结果入栈；当一遍后，栈顶就是表达式的值。因此逆波兰表达式的求值使用堆栈结构很容易实现，并且能很快求值。

注意：逆波兰记法并不是简单的波兰表达式的反转。因为对于不满足交换律的操作符，它的操作数写法仍然是常规顺序，如，波兰记法“/ 6 3”的逆波兰记法是“6 3 /”而不是“3 6 /”；数字的数位写法也是常规顺序

以上内容摘自维基百科：

前缀表达式

三种表达法的相互转换

前缀表达式可以用二叉树的前序遍历得到，中缀表达式可以用二叉树的中序遍历得到，后缀表达式可以用二叉树的后序遍历得到。在转换过程中，始终以操作符作为根节点

例如，对于中缀表达式:

(1 + 2) * (3 + 4)

对应的二叉树为

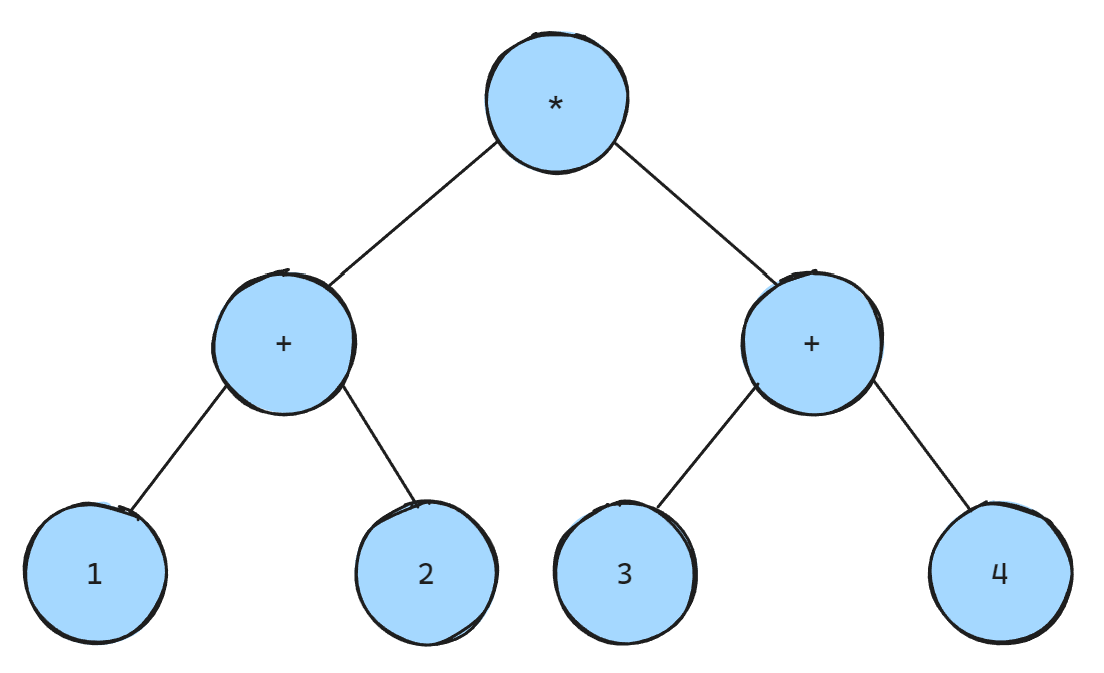
将其转化为前缀表达式为

* + 1 2 + 3 4

将其转化为后缀表达式为

1 2 + 3 4 + *

练习：逆波兰表达式求值

题目链接：150. 逆波兰表达式求值 - 力扣（LeetCode）

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意：
有效的算符为 '+'、 '-'、 '*' 和 '/' 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

思路解析：

对于逆波兰表达式一般用栈的数据结构解决，当表达式中的字符为操作数时，操作数入栈，当表达式中的字符为操作符时，依次弹出两个操作数，进行对应操作符的运算

参考代码：

C语言代码

使用C语言及栈来解决时，需要注意下面的问题

1. 因为题目给的运算式是单个字符串，在比较时需要使用到strcmp函数，而不是直接使用==进行判断
2. 因为*的ASCII值小于其余三个运算符，并且数字可能存在负数，所以在处理减号不入栈时需要处理负数的情况
3. 设计栈时，可以直接使用实际实现的栈数据结构，也可用一个空数组来模拟栈

// 使用C语言和栈解决问题
// 栈的声明
typedef int STDataType;
typedef struct stack
{STDataType* data;int top;      // 栈顶位置int capacity; // 元素个数
} ST;// 栈的初始化
void STInit(ST* st);
// 栈的销毁
void STDestroy(ST* st);
// 数据入栈
void STPush(ST* st, STDataType x);
// 数据出栈
void STPop(ST* st);
// 判断栈是否为空
bool STEmpty(ST* st);
// 获取栈元素
STDataType STTop(ST* st);// 栈的实现
// 栈的初始化
void STInit(ST* st)
{// 判断是否存在队列assert(st);// 初始化队列st->data = NULL;st->top = 0; // 栈顶指针指向存储数据的下一个位置，代表栈内无数据// st->top = -1;//栈顶指针指向存储数据的位置，代表栈内无数据st->capacity = 0;
}// 栈的销毁
void STDestroy(ST* st)
{// 确保有栈的存在assert(st);// 销毁栈free(st->data);st->data = NULL;st->top = st->capacity = 0;
}// 数据入栈
void STPush(ST* st, STDataType x)
{// 确保有栈的存在assert(st);// 向top位置增加数据，并使top向后移动// 需要判断栈的容量大小if (st->top == st->capacity){// 如果栈的空间为0，则开辟四个空间，如果栈容量不为0，则扩容原来容量的2倍int newCapacity = st->capacity == 0 ? 4 : st->capacity * 2;STDataType* tmp = (STDataType*)realloc(st->data, sizeof(STDataType) * newCapacity);assert(tmp);st->data = tmp;st->capacity = newCapacity;}// 数据压栈并改变topst->data[st->top++] = x;
}
// 数据出栈
void STPop(ST* st)
{// 确保有栈的存在assert(st);// 确保栈不会越界assert(!STEmpty(st));// 直接移动top指针，“看不见即删除”st->top--;
}
// 判断栈是否为空
bool STEmpty(ST* st)
{// 确保有栈的存在assert(st);// 栈为空返回真，栈不为空返回假return st->top == 0; // 判断表达式返回值只有1和0，如果为真返回1(true)，如果为假返回0(false)
}
// 获取栈元素
STDataType STTop(ST* st)
{// 确保栈存在assert(st);// 确保栈不为空assert(!STEmpty(st));// top为栈内数据的下一个位置，要获取当前位置的元素需要-1操作return st->data[st->top - 1];
}int evalRPN(char** tokens, int tokensSize) {ST st;STInit(&st);for (int i = 0; i < tokensSize; i++){//当遇到操作数时进栈if (((strcmp(tokens[i], "+") > 0) + (strcmp(tokens[i], "-") >= 0 && atoi(tokens[i]) < 0) + (strcmp(tokens[i], "*") > 0) + (strcmp(tokens[i], "/") > 0)) > 2){STPush(&st, atoi(tokens[i]));}else{//当遇到操作符时出栈运算int num1 = STTop(&st);STPop(&st);int num2 = STTop(&st);STPop(&st);if (strcmp(tokens[i], "+") == 0){STPush(&st, (num2 + num1));}if (strcmp(tokens[i], "-") == 0){STPush(&st, (num2 - num1));}if (strcmp(tokens[i], "*") == 0){STPush(&st, (num2 * num1));}if (strcmp(tokens[i], "/") == 0){STPush(&st, (num2 / num1));}}}int ans = STTop(&st);STPop(&st);return ans;
}

C++代码后续补充……

这篇关于小小算式(1 + 2) * (3 + 4)背后的大道理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---