第十三届蓝桥杯真题解析

本文主要是介绍第十三届蓝桥杯真题解析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：算法从入门到精通
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

修建灌木

算法原理

1.模拟：

解题思路:
我们来模拟一遍很容易发现，一棵树如果想长得最高，就是看爱丽丝隔多长时间来修剪它

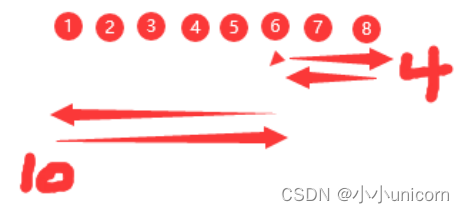
如图，以6为例，一定是往返的时间最长，而往返有两种方式，所以只需要比较两种往返谁大就好了。

其实如果是中间左边的（1 2 3 4），一定是往右往返最大，在中间右边的（5 6 7 8），一定是往左往返最大，但是这个中间数判断有些麻烦，要看总数是奇数还是偶数，又有整形变量精度缺失问题，索性就写个max就做比较了。

代码实现：

#define ll long long
#include<iostream>
using namespace std;
int max(int a,int b)
{return a>b?a:b;
}int main ()
{int i,n;cin>>n;for(i=1;i<=n;i++){cout<<max(i-1,n-i)*2<<endl;}return 0;
}

2.找规律

代码实现：

#include<iostream>using namespace std;int main()
{int n;int a[10005];scanf("%d", &n);if (n % 2 == 0)//n为偶数的时候{for (int i = 1; i <= n / 2; i++){a[i] = (2 * (n - i));cout << a[i] << endl;//printf("%d\n", a[i]);}for (int j = n / 2 + 1; j <= n; j++){a[j] = a[n + 1 - j];cout << a[j] << endl;//printf("%d\n", a[j]);}}if (n % 2 != 0)//n为奇数的时候{for (int i = 1; i <= n / 2; i++){a[i] = 2 * (n - i);cout << a[i] << endl;//printf("%d\n", a[i]);}//printf("%d\n", n - 1);cout<<n-1<<endl;for (int j = n / 2 + 2; j <= n; j++){a[j] = a[n + 1 - j];cout << a[j] << endl;//printf("%d\n", a[j]);}}return 0;
}

刷题统计：

算法原理：

1.暴力（80分）

直接将结果枚举出来

代码实现：

#include<iostream>
using namespace std;
typedef long long ll;
int main()
{ll a, b, n;cin >> a >> b >> n;ll ret = 0;ll day = 0;for(ll j=0;;j++){//一周for (ll i = 0; i < 7; i++){if (i <= 4){ret += a;day++;}else{ret += b;day++;}if (ret >= n)break;}if (ret >= n)break;}cout << day << endl;return 0;
}

但是当样例过大时会超时。

2.计算：

先用ans表示有多少周，n/(5a+b2)

工作日有二天，周末有二天

sum表示天数

用n-（5a+2b）*ans=剩余的天数

剩余的天数一定会落在工作日，或者周末这两种情况；

再用(n-(5a+2b)*ans)/a表示能在工作日完成的a题，

如果(n-(5a+2b)*ans)%a 不等于0，说明有剩余，还要加一天

在周末这种情况也同理；

代码实现：

//满分做法
#include<iostream>
using namespace std;
typedef long long ll;
int main()
{ll a, b, n;cin >> a >> b >> n;ll ans, sum = 0;//先看有多少周ans = n / (a * 5 + b * 2);ll m = a * 5 + b * 2;//剩余天数ll residue=n-m*ans;//天数=周数*7sum = ans * 7;//剩余天数<=工作日的工作量(落在工作日)if (residue<= 5 * a){//能被工作日弄完sum += residue / a;//不能弄完if (residue % a != 0){sum++;}}//落在周末else{//先把前面5天工作日加上sum += 5;//看剩余天数sum += (residue - 5 * a) / b;if ((residue - 5 * a) % b != 0){sum++;}}cout << sum;return 0;
}

X进制减法

算法原理：

解题思路:10 4 0->1052+4*2=108.

因此A=a[i]*pr+a[i-1]*p[r-1]+……a[0];
注意事项:

数据非常大，必须边求边累加，直接累加最后相减会出现问题
代码实现：

#include<iostream>
#include<cstring>
using namespace std;
int p(int a,int b,int c)
{return (a>b?a:b)>c?(a>b?a:b):c;
}
int main()
{int n,m,l,a[100001],b[100001];long long res=0;memset(a,0,sizeof(a));memset(b,0,sizeof(b));cin>>l>>n;for(int i=n;i>0;i--)cin>>a[i];cin>>m;for(int i=m;i>0;i--)cin>>b[i];for(int i=n;i>1;i--){res=((res+a[i]-b[i])*p(a[i-1]+1,b[i-1]+1,2))%1000000007;}res+=a[1]-b[1];cout<<res<<endl;return 0;
}

统计子矩阵：

算法原理：

/解题思路/

/使用双指针 将A数组中的任意俩列的前缀和看做一个一维数组求解/

/在一维数组中 a[n]={a[1],a[2],…,a[n]}; 类似题目 求其中不大于k:9的数组矩阵个数/

那么有俩个指针i j 开始时同时指向a[1]:1

sum=a[i]加到a[j]

sum比k小 则j++即j后移

比k大 则i++即i后移

sum比k大时,此时产生的数组数为(i-j)

代码实现：

#include<bits/stdc++.h>
using namespace std;
int a[520][520];
int s[520][520];  //A数列每行的前缀和 
int main()
{long long count=0;int k,m,n; cin>>n>>m>>k;
/*输入A数列 同时求前缀和*/for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>a[i][j]; s[i][j]=s[i][j-1]+a[i][j];}
/*数据处理*/for(int j1=1;j1<=m;j1++)for(int j2=j1;j2<=m;j2++) //j1 j2 表示所要枚举的列数 {int j=1,sum=s[1][j2]-s[1][j1-1]; //sum表示s数组的累加 for(int i=1;i<=n;i++){while(sum<=k && j<=n) {j++; sum+=s[j][j2]-s[j][j1-1];} count+=j-i;sum-=s[i][j2]-s[i][j1-1]; //当sum>k时,i后移,同时要减去上一个值 }}cout<<count;return 0;
}

积木画

算法原理：

首先这个题肯定是用动态规划来做的,正好它也符合动态规划做题的思想,无后效性也满足所以我们用动态规划做会好做一点.
那怎么想这个题呢,首先它是二维的一个矩阵模式,并且有摆放还是有顺序的,所以我们如果要用二维dp来做还确实不好做,拿我们所幸直接用一维来简化拼积木的过程,但是怎么简化呢.

我们先来看下题目给的案例:

首先我们直接来看三阶的,第一个和第二个我们可以发现I型积木拼放的方式是有2种的,或者看一和四都行,然后L型积木的拼接方式是1种看三和五(你把他们两个反转过来就是一种),那我们不妨想的简单一点所以递推公式就是:$dp[i]=dp[i-1]\ast 2+dp[i-3]$;

证明的方法就是我们刚才的思想过程,我们讲二维的矩阵看成了一维的,所以I型积木就是等于1个方格,所以我们记为i-1,L型积木就是等于1.5个方格,但是L型积木不能单独出现,必须成双的出现,所以我们记为i-3,又由于I型积木出现在一个位置有两种方式,所以我们乘以二,L型积木出现只有一直方式我们乘以1,就结束了。

但是我们还要进行初始化前三个:

当i等于1的时候dp就是1,这个没啥说的,只能放一种I型不管咋放都一样.
当i等于2的时候dp是2,因为可以放两个I型,可以水平放可以竖直放2种.
当i等于3的时候就是题目当中的情况dp等于5,

代码实现：

#include<stdio.h>
#include<string.h>
#include<iostream>
#incldue<vector>
using namespace std;
#define mod 1000000007
int dp[10000005];
int main()
{int n;cin>>n;vector<int> dp(10000005,0);dp[1]=1,dp[2]=2,dp[3]=5;for(int i=4;i<=n;i++){dp[i]=(dp[i-1]*2%mod+dp[i-3]%mod)%mod;}cout<<dp[n];return 0;
}

这篇关于第十三届蓝桥杯真题解析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---